2022-2023学年华师大版数学九年级上册---相似三角形的性质-课件

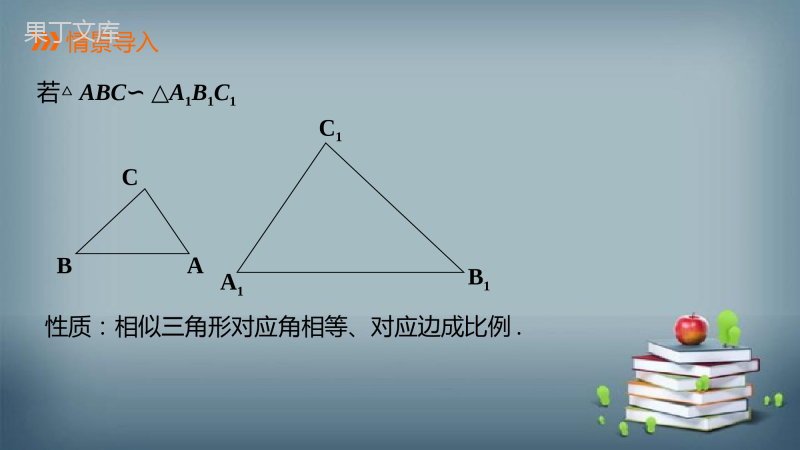
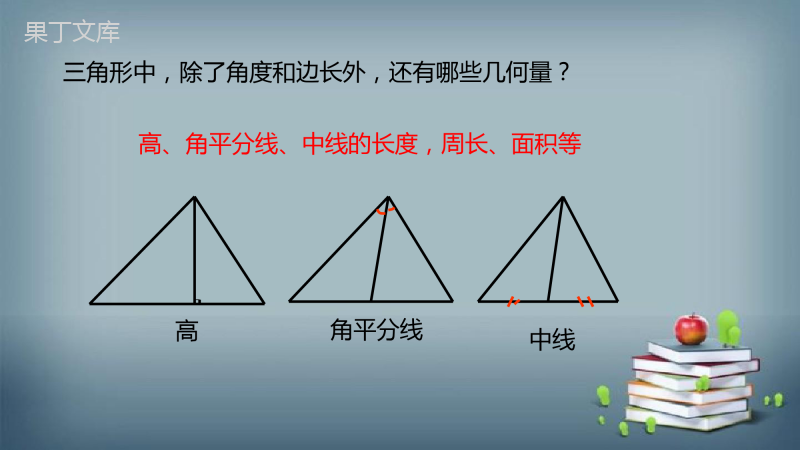
23.3.3相似三角形的性质教学目标1.在对相似三角形的原有认知的基础上，进一步探究相似三角形的其它性质.2.通过观察、思考、发现相似三角形的性质，包括相似三角形对应边上的高、中线、对应角的角平分线还有周长之比等于相似比，面积之比等于相似比的平方；能用演绎推理加以证明，并能运用这些性质进行简单的计算与说理.3.经历探索相似三角形性质的过程，体验研究数学问题的一般方法和转化的数学思想，提高学生的逻辑思维能力和解决问题的能力.教学重难点1.探索并证明相似三角形的其它性质.2.能根据相似三角形的这些性质解决简单的数学问题.情景导入ACBA1C1B1性质：相似三角形对应角相等、对应边成比例.若△ABC∽△A1B1C1三角形中，除了角度和边长外，还有哪些几何量？高、角平分线、中线的长度，周长、面积等高角平分线中线A'B'D'C'ABCDA'B'C'E'ABCE相似三角形的对应线段之间有什么数量上的关系呢？获取新知△ABD和△A'B'D'都是直角三角形，且∠B=∠B'，因为有两个角对应相等，所以这两个三角形相似.因此''''.ADABkADAB结论1.相似三角形对应边上的高的比等于相似比一、相似三角形对应边上的高的比等于相似比''''.ADABkADAB二、相似三角形对应的中线的比等于相似比已知：△ABC∽△A′B′C′，相似比为k，AD、A′D′分别是△ABC、△A′B′C′的中线，求证：''ADkAD证明：∵△ABC∽△A′B′C′.∴∠B=∠B′．又AD,A'D′分别为对应边的中线.∴△ABD∽△A′B′D′.''''ABBCABBC''''ABBDABBD''''ADABkADABA'B'D'C'ABCD''ADkAD''''ABBCABBC''''ABBDABBD''''ADABkADAB三、相似三角形对应角的平分线的比等于相似比''''''.ABBCCAkABBCCAA'B'C'E'ABCE已知：△ABC∽△A′B′C′，相似比为k，即且BE,B′E′是角的平方线，求证：''BEkBE证明：∵△ABC∽△A′B′C′∴∠A′B′C′=A∠BC,∠B′A′C′=∠BAC．又BE,B′E′分别为对应角的平方线∴∠ABE=∠A′B′E′.∴△ABE∽△A′B′E′.''''BEABkBEAB''''''.ABBCCAkABBCCA''BEkBE''''BEABkBEAB四、相似三角形周长的比等于相似比证明：设△ABC∽△A1B1C1，相似比为k，111111,,,ABkABBCkBCCAkCA求证：相似三角形的周长比等于相似比.ABCA1B1C1111111ABBCCAkABBCCA11111111111111111kABkBCkCAABBCCAkABBCCAABBCCA111111,,,ABkABBCkBCCAkCA111111ABBCCAkABBCCA11111111111111111kABkBCkCAABBCCAkABBCCAABBCCA五、相似三角形面积的比等于相似比的平方证明：设△ABC∽△A′B′C′，相似比为k,如图，分别作出△ABC和△A′B′C′的高AD和A′D′.∵△ABC∽△A′B′C′.''.ADBCkADBC212.12ABCABCBCADSBCADkkkSBCADBCAD△△ABCA′B′C′DD′''.ADBCkADBC212.12ABCABCBCADSBCADkkkSBCADBCAD△△1.相似三角形对应边上的高的比等于相似比．2.相似三角形对应边上的中线的比等于相似比．3.相似三角形对应角的平分线的比等于相似比．4.相似三角形的周长之比等于相似比；5．相似三角形面积的比等于相似比的平方；易错警示：利用相似三角形的性质时，要注意“对应”两字，要找准对应线段．例题讲解例1如图，AD是△ABC的高，AD=h，点R在AC边上，点S在AB边上，SR⊥AD，垂足为E.当SR=BC时，求DE的长.如果SR=BC呢？13121312解：∵SR⊥AD，BC⊥AD,∴SR∥BC.∴∠ASR=∠B，∠ARS=∠C.∴△ASR∽△ABC(两角分别相等的两个三角形相似）.(相似三角形对应高的比等于相似比），当SR=BC时，得解得DE=h.当SR=BC时，得解得DE=h.AESRADBC.ADDESRADBC即121.2hDEh1.3hDEh121323例2已知：如图，□ABCD中，E是BC边上一点，且BE＝EC，BD，AE相交于F点．(1)求△BEF的周长与△AFD的周长之比；(2)若△BEF的面积为6cm2，求△AFD的面积．1212解：(1)∵四边形ABCD是平行四边形，∴BC∥AD，BC＝AD.∴△BEF∽△DAF.∵BE＝EC，∴BE∶DA＝BE∶BC＝13.∶∴△BEF的周长与△AFD的周长之比为13.∶(2)由(1)可知△BEF与△AFD的相似比为∴S△BEF∶S△AFD＝19.∶又∵S△BEF＝6cm2，∴S△AFD＝54cm2.12131213随堂演练1.如果两个相似三角形对应边的比为23∶，那么这两个相似三角形面积的比是()A．23∶B.C．49∶D．827∶23：C23：2.如图，△ABC∽△A′B′C′，AD，BE分别是△ABC的高和中线，A′D′，B′E′分别是△A′B′C′的高和中线，且AD＝4，A′D′＝3，BE＝6，则B′E′的长为()3579....2222ABCDD3579....2222ABCD3.如图是一个照相机成像的示意图，如果底片AB宽40mm，焦距是60mm，求所拍摄的2m外景物的宽CD.解：由题意，可知△ABE∽△DCE，答：所拍摄的2m外景物的宽CD为0.040.064,23CDmCD解得0.040.064,23CDmCD解得4.已知△ABC∽△A'B'C',,AB边上的中线CD=4cm,△ABC的周长为20cm,△A'B'C'的面积为64cm2,求:(1)A'B'边上的中线C'D'的长;(2)△A'B'C'的周长;(3)△ABC的面积.''12ABAB''12ABAB''''''''''''''''''''2''21,812022=4013,46416ABCABCABCABCABCABCABCABCCDABCDcmCDABCABCABCCcmSSABSABScm解：''''''''''''''''''''2''21,812022=4013,46416ABCABCABCABCABCABCABCABCCDABCDcmCDABCABCABCCcmSSABSABScm解：课堂小结相似三角形的性质相似三角形对应线段的比等于相似比（高、中线、角平分线）相似三角形周长比等于相似比相似三角形面积的比等于相似比的平方（反之，为算术平方根）