《离散型随机变量的方差》人教版高中数学选修2-3PPT课件（第2.3.2课时）.pptx

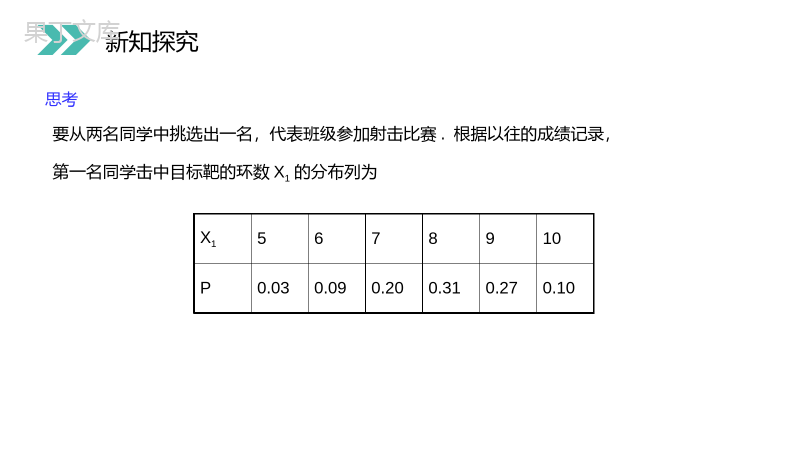
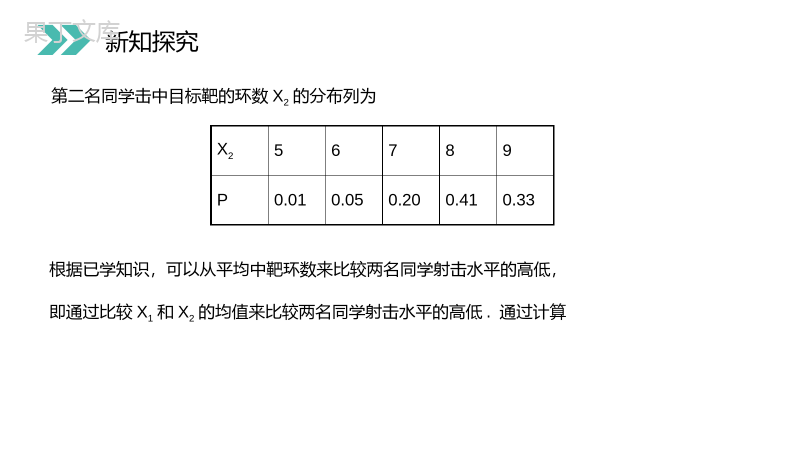
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-32.3.2离散型随机变量的方差第2章随机变量及其分布人教版高中数学选修2-31.离散型随机变量X的均值均值反映了离散型随机变量取值的平均水平.2.两种特殊分布的均值（1）若随机变量X服从两点分布，则EX=p.（2）若X~B(n，p)，则EX=np.niii=1EX=xp课前导入niii=1EX=xp数学期望是离散型随机变量的一个特征数，它反映了离散型随机变量取值的平均水平，表示了随机变量在随机实验中取值的平均值，所以又常称为随机变量的平均数、均值.今天，我们将对随机变量取值的稳定与波动、集中与离散的程度进行研究.课前导入思考要从两名同学中挑选出一名，代表班级参加射击比赛.根据以往的成绩记录，第一名同学击中目标靶的环数X1的分布列为X15678910P0.030.090.200.310.270.10新知探究第二名同学击中目标靶的环数X2的分布列为X256789P0.010.050.200.410.33根据已学知识，可以从平均中靶环数来比较两名同学射击水平的高低，即通过比较X1和X2的均值来比较两名同学射击水平的高低.通过计算新知探究E(X1)=8，E(X2)=8，发现两个均值相等，因此只根据均值不能区分这两名同学的射击水平.思考除平均中靶环数外，还有其他刻画两名同学各自射击特点的指标吗？新知探究图(1)(2)分别表示X1和X2的分布列图.比较两个图形，可以发现，第二名同学的射击成绩更集中于8环，即第二名同学的射击成绩更稳定.O5671098P1X0.10.20.30.40.5O56798P2X0.10.20.30.40.5(1)(2)怎样定量刻画随机变量的稳定性?新知探究1X2X1.方差设离散型随机变量X的分布列为知识要点Xx1x2…xi…xnPp1p2…pi…pn则(xi-E(X))2描述了xi(i=1，2，…，n)相对于均值E(X)的偏离程度.新知探究为这些偏离程度的加权平均，刻画了随机变量X与其均值EX的平均偏离程度.我们称DX为随机变量X的方差(variance).其算术平方根为随机变量X的标准差(standarddeviation).记为n2iii=1DX=(x-EX)pDXσX随机变量的方差和标准差都反映了随机变量取值偏离于均值的平均程度.方差或标准差越小，则随机变量偏离于均值的平均程度越小.新知探究n2iii=1DX=(x-EX)pDXσX说明：随机变量集中的位置是随机变量的均值；方差或标准差这种度量指标是一种加权平均的度量指标.思考随机变量的方差与样本的方差有何联系与区别?新知探究随机变量的方差是常数，而样本的方差是随着样本的不同而变化的，因此样本的方差是随机变量.对于简单随机样本，随着样本容量的增加，样本方差越来越接近总体方差，因此常用样本方差来估计总体方差.现在，可以用两名同学射击成绩的方差来刻画他们各自的特点，为选派选手提供依据.由前面的计算结果及方差的定义，得10211i=5DX=(i-8)P(X=i)=1.50,9222i=5DX=(i-8)P(X=i)=0.82因此第一名同学的射击成绩稳定性较差，第二名同学的射击成绩稳定性较好，稳定于8环左右.新知探究10211i=5DX=(i-8)P(X=i)=1.50,9222i=5DX=(i-8)P(X=i)=0.82知识要点2.几点重要性质（1）若X服从两点分布，则D(X)=p(1-p);（2）若X~B(n，p)，则D(X)=np(1-p);（3）D(aX+b)=a2D(X).新知探究例题1A、B两台机床同时加工零件，每生产一批数量较大的产品时，出次品的概率如下表所示：次品数ξ10123概率P0.70.20.060.04次品数ξ10123概率P0.80.060.040.10问哪一台机床加工质量较好？新知探究解：Eξ1=0×0.7+1×0.2+2×0.06+3×0.04=0.44,Eξ2=0×0.8+1×0.06+2×0.04+3×0.10=0.44.它们的期望相同，再比较它们的方差Dξ1=(0-0.44)2×0.7+(1-0.44)2×0.2+(2-0.44)2×0.06+(3-0.44)2×0.04=0.6064,Dξ2=(0-0.44)2×0.8+(1-0.44)2×0.06+(2-0.44)2×0.04+(3-0.44)2×0.10=0.9264.∴Dξ1