《复数的几何意义》人教版高中数学选修1-2PPT课件（第3.1.2课时）.pptx

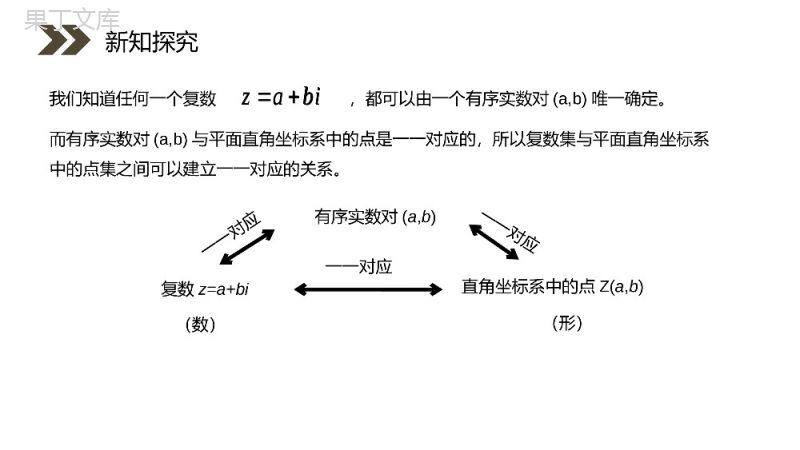
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE1-23.1.2复数的几何意义第3章数系的扩充与复数的引入人教版高中数学选修1-21.对虚数单位i的规定①i2=-1；②可以与实数一起进行四则运算.2.复数z=a+bi(其中a、bR)中a叫z的、b叫z的.实部虚部z为实数、z为纯虚数.b=000ba上节我们学习了数系的扩充和复数的概念，我们知道数系的每一次扩充都与实际需求是相关的，为了解方程的需要，我们又引入了一个新数i，从而将实数系扩充到复数系，而这个新的数i满足一定的特征：思考如何从几何的角度理解复数呢？课前导入00ba我们知道，实数与数轴上的点是一一对应的，因此，实数可以用数轴上的点来表示，类比实数的几何意义，复数的几何意义是什么呢？课前导入Z=a+bi(a,b∈R)实部!虚部!课前导入复数的一般形式？一个复数由什么唯一确定？复数z=a+bi有序实数对(a,b)（数）（形）一一对应一一对应一一对应我们知道任何一个复数，都可以由一个有序实数对(a,b)唯一确定。biaz直角坐标系中的点Z(a,b)而有序实数对(a,b)与平面直角坐标系中的点是一一对应的，所以复数集与平面直角坐标系中的点集之间可以建立一一对应的关系。新知探究biaz这是复数的一种几何意义.xy0Z(a,b)建立了平面直角坐标系来表示复数的平面——复平面x轴——实轴y轴——虚轴abz=a+bi显然，实轴上的点都表示实数；除原点外，虚轴上的点都表示纯虚数。),(复平面内的点复数一一对应baZbiaz新知探究这是复数的一种几何意义.),(复平面内的点复数一一对应baZbiaz例：你能说出下列复数所对应的点的坐标吗？并说出点的位置？iz54)1(iz2)2(2)3(z23)4(iiz位于第四象限)5,4(位于虚轴上)2,0(位于实轴上)0,2(iiz33)1,3(新知探究iz54)1(iz2)2(2)3(z23)4(iiz位于第四象限)5,4(位于虚轴上)2,0(位于实轴上)0,2(iiz33)1,3(0283015822mmmm解：4735mmm或37m①②0283015822mmmm4753mmm或4m总结根据复数与复平面内点的对应关系，由复数在平面内对应点所在的象限从而确定实部和虚数组成的不等式组，然后进行求解。新知探究题型一复平面例当实数m为何值时，复数(m2－8m＋15)＋(m2＋3m－28)i在复平面内的对应点①位于第四象限；②位于x轴的负半轴上.0283015822mmmm解：4735mmm或37m0283015822mmmm4753mmm或4m思考题1(1)在复平面内，复数z＝sin2＋icos2对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【解析】∵sin2>0，cos2<0，∴复数对应的点在第四象限，选D.【答案】D新知探究xy0Z(a,b)abz=a+bi这是复数的又一种几何意义.复数的几何意义复数z可由有序实数对（a,b)来表示也可以由有序实数对向量OZOZbiaz平面向量复数一一对应为了方便起见，我们常把复数说成点Z或说成向量，并且规定，相等的向量表示同一个复数biazOZ我们知道每一个平面向量都可以用一个有序实数对来表示，而有序实数对与复数也是一一对应的。这样，我们就可以用平面向量来表示复数。（a,b)来表示新知探究也可以由有序实数对向量OZOZbiaz平面向量复数一一对应biazOZ三、复数的摸xyobaZ(a,b)z=a+bi向量的模叫做复数z=a+bi的模，记做OZzabi或复数的模的几何意义：复数z=a+bi在复平面所对应的点Z（a，b）到原点的距离22zOZab如何求复数的模？？新知探究OZzabi或22zOZab22sincos1(）解析：zcos2221cos14cos220)2,0(z新知探究题型二复数的模例2求复数z＝1＋cosα＋isinα(π<α<2π)的模的取值范围.探究2求复数z＝a＋bi(a，b∈R)的模，只需代入定义式z＝即可，注意复数的模往往和其他章节的内容相联系.22sincos1(）解析：zcos2221cos14cos220)2,0(z),()1(Ryxyixz设解析：22yxz则2122yx由题意得4122yx所以，复数z对应的点z的集合是以原点O为圆心，以1和2为半径的两圆所形成的圆环，不包括边界。（2）根据模的几何意义z-i=1表示复数z对应的点到复数i对应的点（0，1）的距离为1。所以，满足｜z-i=1的点z的集合是以（0，1）为圆心，1为半径的圆。题型三轨迹问题例3设z∈C，且满足下列条件，在复平面内，复数z对应的点Z的集合是什么图形？(1)1