《导数的概念》人教版高中数学选修2-2PPT课件（第1.1.2课时）.pptx

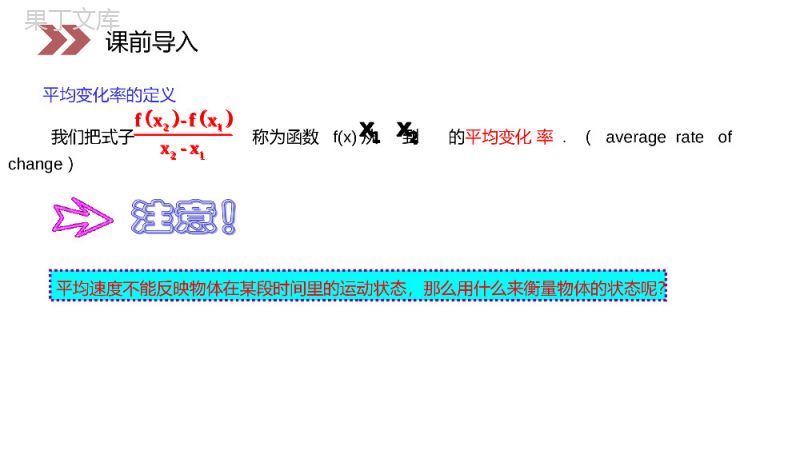
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-21.1.2导数的概念第1章导数及其应用人教版高中数学选修2-2平均变化率的定义我们把式子称为函数f(x)从到的平均变化率.（averagerateofchange）2121fx-fxx-x1x2x课前导入平均速度不能反映物体在某段时间里的运动状态，那么用什么来衡量物体的状态呢？2121fx-fxx-x1x2x如何知道运动员在每一时刻的速度呢？课前导入汽车在每一刻的速度怎么知道呢？课前导入思考在高台跳水运动中，运动员在不同时刻的速度是不同的.我们把物体在某一时刻的速度称为瞬时速度（instaneousvelociy）.新知探究瞬时速度的概念平均速度反映了物体运动时的快慢程度,但要精确地描述非匀速直线运动,就要知道物体在每一时刻运动的快慢程度,也即需要通过瞬时速度来反映.瞬时速度与平均速度的区别例题1已知物体作变速直线运动,其运动方程为s＝s（t）(ｓ表示位移,t表示时间）,求物体在t0时刻的速度．OA0A1sss(t)s=新知探究00()()limlim.ttssttstvtt物体的运动规律是s=s(t)，那么物体在时刻t的瞬时速度v，就是物体在t到t+Δt这段时间内，当Δt-0时的平均速度:00()()limlim.ttssttstvtt物体作自由落体运动,运动方程为：其中位移单位是m，时间单位是s，g=10m/s2.求：（1）物体在时间区间[2，2.1]上的平均速度；（2）物体在t=2(s)时的瞬时速度.例题221s=gt2新知探究21s=gt2sss(2+t)Os(2)解:__Δs1v==2g+g(Δt)Δt2(1)将Δt=0.1代入上式，得:__v=2.05g=20.5m/s.新知探究__Δs1v==2g+g(Δt)Δt2__v=2.05g=20.5m/s.(2)Δt0,2+Δt2当./202limlim0__0smgtsvvtt即物体在时刻t0=2(s)的瞬时速度等于20(m/s).当时间间隔Δt逐渐变小时,平均速度就越接近t0=2(s)时的瞬时速度v=20(m/s).从而平均速度的极限为v新知探究(2)Δt0,2+Δt2当./202limlim0__0smgtsvvttv还记得上节课讲的关于高台跳水问题吗？运动员相对于水面的高度h(单位：米)与起跳后的时间t（单位：秒）存在函数关系:2h(t)=-4.9t+6.5t+10例题3新知探究2h(t)=-4.9t+6.5t+10通过列表看出平均速度的变化趋势：知道了瞬时速度的概念，那么在高台跳水运动中，如何求（比如，t=2)运动员的瞬时速度？新知探究△t<0时，在[2+t,2]△这段时间内2222hhtvt24.9Δt+13.1Δt=-Δt=-4.9Δt-13.1当△t=-0.01时，=-13.051；v当△t=-0.001时，=-13.0951；v当△t=-0.0001时，=-13.09951；v当△t=-0.00001时，=-13.099951；v当△t=-0.000001时，=-13.0999951；v…...2222hhtvt24.9Δt+13.1Δt=-Δt=-4.9Δt-13.1vvvvv△t>0时，在[2,2+t]△这段时间内h2-h2+Δtv=2-2+Δt24.9Δt+13.1Δt=-Δt=-4.9Δt-13.1当△t=0.01时，=-13.149；v当△t=0.001时，=-13.1049；v当△t=0.0001时，=-13.10049；v当△t=0.00001时，=-13.100049；v当△t=0.000001时，=-13.1000049；v…...新知探究h2-h2+Δtv=2-2+Δt24.9Δt+13.1Δt=-Δt=-4.9Δt-13.1vvvvv观察当趋近于0时，平均速度有什么样的变化？tv我们发现，当趋近于0时，即无论t从小于2的一边，还是从大于2的一边趋近于2时，平均速度都趋近于一个确定的值-13.1.Δt新知探究我们用表示“当t=2,Δt趋近于0时,平均速度趋于确定值-13.1”.0limth(2+Δt)-h(2)=-13.1ΔttvΔt0limth(2+Δt)-h(2)=-13.1Δt探究那么运动员在某一时刻t0的瞬时速度怎么表示?0limt00h(t+Δt)-h(t)Δt新知探究0limt00h(t+Δt)-h(t)Δt探究函数y=f(x)在x=x0处的瞬时变化率又怎么表示？新知探究一般地，函数在处的瞬时变化率是y=fx0x=x我们称它为函数在处的导数（derivative）.yfx0xx0000limlimxxfxxfxfxx新知探究导数定义y=fx0x=xyfx0xx0000limlimxxfxxfxfxx一般将导数记作,或者,即0f(x)0xxy(Δ))00000Δx0xx0fxxf(x)f(xf(x)f(x)limlimΔxxx表示函数y关于自变量x在处的导数0xxy新知探究0f(x)0xxy(Δ))00000Δx0xx0fxxf(x)f(xf(x)f(x)limlimΔxxx0xxy0xxy有极限f(x)在点x0处可导f(x)在点x0处的导数新知探究概念理解0xxy是函数f(x)在以x0与x0+Δx为端点的区间[x0,x0+Δx](或[x0+Δx,x0])上的平均变化率,而导数则是函数f(x)在点x0处的变化率,它反映了函数随自变量变化而变化的快慢程度．00f(xΔx)f(x)ΔyΔxΔx概念理解新知探究00f(xΔx)f(x)ΔyΔxΔx000xx0f(x)-f(x)f(x)=limx-x事实上，导数也可以用下式表示：新知探究知识补充如果函数y=f(x)在点x=x0存在导数，就说函数y=f(x)在点x0处可导，如果极限不存在，就说函数f(x)在点x0处不可导.000xx0f(x)-f(x)f(x)=limx-x由导数的意义可知，求函数y=f(x)在点x0处的导数的基本方法是:（1）求函数的增量00Δy=f(x+Δx)-f(x)..00f(x+Δx)-f(x)Δy=ΔxΔx（2）求平均变化率0Δx0Δyf(x)=lim.Δx（3）取极限，求得导数新知探究注意！这里的增量不是一般意义上的增量，它可正也可负.自变量的增量Δx的形式是多样的,但不论Δx选择哪种形式,Δy也必须选择与之相对应的形式00Δy=f(x+Δx)-f(x)..00f(x+Δx)-f(x)Δy=ΔxΔx0Δx0Δyf(x)=lim.Δx已知函数在处的附近有定义，且，求的值.y=x0x=x0x=x1y'=20x课堂练习00解:∵Δy=x+Δx-x,0000000000x+Δx-x(x+Δx-x)(x+Δx+x)Δy∴==ΔxΔxΔx(x+Δx+x)1=.x+Δx+xΔx→0Δx→0000Δy11∴lim=lim=,Δxx+Δx+x2x0x=x00111由y'=,得=,∴x=1.222xy=x0x=x0x=x1y'=20x00解:∵Δy=x+Δx-x,0000000000x+Δx-x(x+Δx-x)(x+Δx+x)Δy∴==ΔxΔxΔx(x+Δx+x)1=.x+Δx+xΔx→0Δx→0000Δy11∴lim=lim=,Δxx+Δx+x2x0x=x00111由y'=,得=,∴x=1.222x例题4求函数y=x2在x=1处的导数.222解：(1)Δy=(1+Δx)-1=2Δx+(Δx),2Δy2Δx+(Δx)==2+Δx,ΔxΔxx=1Δx→0Δx→0Δy∴lim=lim(2+Δx)=2,∴y=2.Δx课堂练习222解：(1)Δy=(1+Δx)-1=2Δx+(Δx),2Δy2Δx+(Δx)==2+Δx,ΔxΔxx=1Δx→0Δx→0Δy∴lim=lim(2+Δx)=2,∴y=2.Δx求函数y=x+1/x在x=2处的导数.11-Δx解：Δy=(2+Δx)+-(2+)=Δx+2+Δx22(2+Δx)-ΔxΔx+Δy12(2+Δx)==1-,ΔxΔx2(2+Δx)x=2Δx→0Δx→0Δy1133∴lim=lim[1-]=1-=,∴y=.Δx2(2+Δx)444课堂练习11-Δx解：Δy=(2+Δx)+-(2+)=Δx+2+Δx22(2+Δx)-ΔxΔx+Δy12(2+Δx)==1-,ΔxΔx2(2+Δx)x=2Δx→0Δx→0Δy1133∴lim=lim[1-]=1-=,∴y=.Δx2(2+Δx)444设函数f(x)在点x0处可导,求下列极限值.00Δx0f(x-Δx)-f(x)lim.Δx→0000Δx→0Δx→0'0f(x-Δx)-f(x)f(x-Δx)-f(x)1)原式=lim=-lim-(-Δx)-解：(Δx=-f(x);课堂练习x→0Δy所以，f(3)=lim=-1Δx同理：f(5)=3′′说明在第3h附近，原油的温度大约以1/h℃的速率下降，原油温度以大约以3/h℃的速率上升.00Δx0f(x-Δx)-f(x)lim.Δx→0000Δx→0Δx→0'0f(x-Δx)-f(x)f(x-Δx)-f(x)1)原式=lim=-lim-(-Δx)-解：(Δx=-f(x);x→0Δy所以，f(3)=lim=-1Δx同理：f(5)=3′′1.瞬时速度的定义物体在某一时刻的速度称为瞬时速度.课堂小结2.导数的定义一般地，函数在处的瞬时变化率是yfx0xx00Δx0Δx0fx+Δx-fxΔflim=limΔxΔx我们称它为函数在处的导数（derivative）.yfx0xxyfx0xx00Δx0Δx0fx+Δx-fxΔflim=limΔxΔxyfx0xx感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-2感谢你的聆听第1章导数及其应用人教版高中数学选修2-2