《平面与平面垂直的性质定理》人教版高中数学必修二PPT课件（第2.3.4课时）.pptx

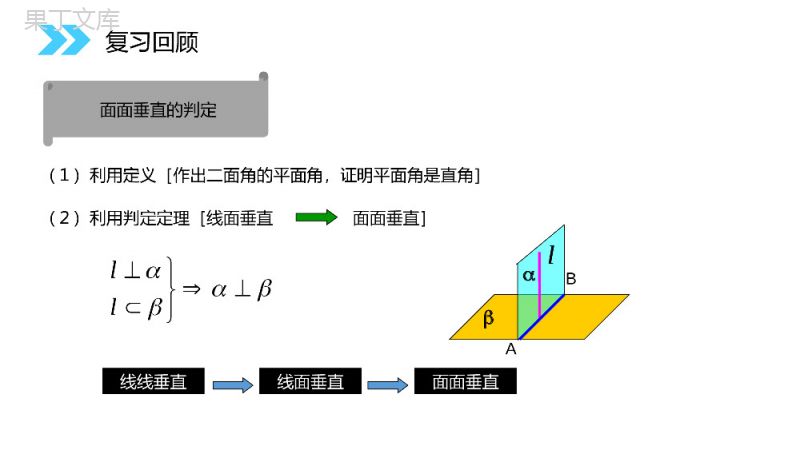
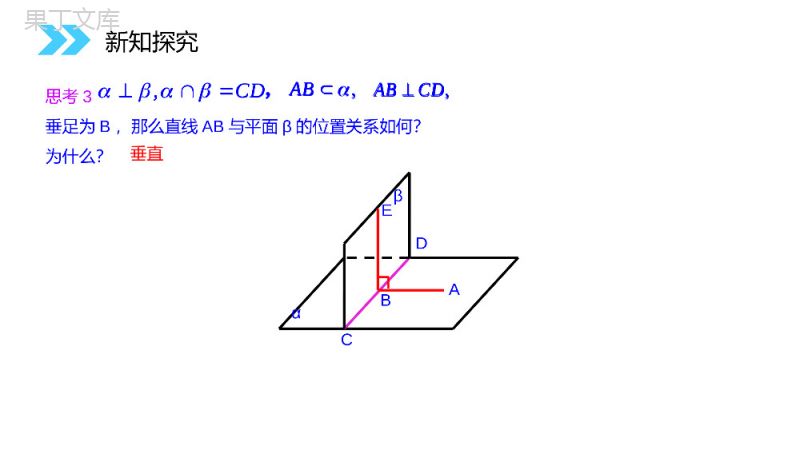
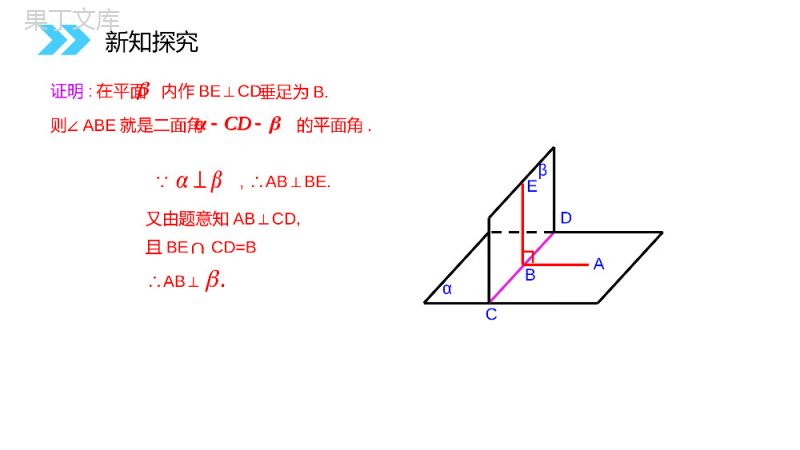
讲解人：办公资源时间：2020.6.1MENTALHEALTHCOUNSELINGPPT2.3.4平面与平面垂直的性质第2章关系点、直线、平面之间的位置关系人教版高中数学必修二（１）利用定义［作出二面角的平面角，证明平面角是直角］（２）利用判定定理［线面垂直面面垂直］lllAB线面垂直面面垂直线线垂直面面垂直的判定复习回顾lllA1D1B1C1CBADαβEF思考2如图，长方体中，α⊥β,(1)α里的直线都和β垂直吗？(2)什么情况下α里的直线和β垂直？与AD垂直不一定新知探究思考3垂足为B，那么直线AB与平面β的位置关系如何？为什么？,CDI，,ABαβABDCE,ABCD垂直新知探究,CDI，,AB,ABCD∵,ABBE.∴⊥又由题意知ABCD,⊥且BECD=B垂足为B.∴AB⊥.则∠ABE就是二面角的平面角.CD证明:在平面内作BECD,⊥αβABDCE新知探究.CD平面与平面垂直的性质定理符号表示:CDABABABCDABCDBDCAB两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直．新知探究CDABABABCDABCDB（线是一个平面内垂直于两平面交线的一条直线）面面垂直线面垂直作用：①它能判定线面垂直.②它能在一个平面内作与这个平面垂直的垂线.关键点：①线在平面内.②线垂直于交线.DCAB提升总结：新知探究思考4设平面⊥平面，点P在平面内，过点P作平面的垂线a，直线a与平面具有什么位置关系?aa直线a在平面内βαPβαP新知探究B.5AABIaaa已知平面，，直线∥，，试判断直线与思的位置关系考αβAbalB垂直新知探究B.5AABIaaa已知平面，，直线∥，，试判断直线与思的位置关系考分析：作出图形.abαβlγmnabαβlγnmA（法二）,.ll例2.已知平面，，满足，，求证：（法一）新知探究,.ll例2.已知平面，，满足，，求证：在α内作直线a⊥n证法1：设在β内作直线bm⊥,,nm//baab//bblαβlγabmnab同理//.blbll新知探究,,nm//baab//bblab同理//.blbll在γ内过A点作直线an⊥，证法2：设在γ内过A点作直线bm⊥，nanalalbl同理abA.l在γ内任取一点A（不在m,n上），abαβlγnmA,,nm新知探究nanalalblabA.l,,nm如果两个相交平面都垂直于另一个平面，那么这两个平面的交线垂直于这个平面.结论αβγl判断线面垂直的两种方法：①线线垂直→线面垂直；②面面垂直→线面垂直.如图：新知探究两个平面垂直应用举例例题1如图4，AB是⊙O的直径，点C是⊙O上的动点，过动点C的直线VC垂直于⊙O所在平面，D、E分别是VA、VC的中点，直线DE与平面VBC有什么关系？试说明理由．解：由VC垂直于⊙O所在平面，知VCAC⊥，VCBC⊥，即∠ACB是二面角A-VC-B的平面角．由∠ACB是直径上的圆周角，知∠ACB=90°。因此，平面VAC⊥平面VBC．由DE是△VAC两边中点连线，知DEAC∥，故DEVC⊥．由两个平面垂直的性质定理，知直线DE与平面VBC垂直。注意：本题也可以先推出AC垂直于平面VBC，再由DE∥AC，推出上面的结论。新知探究例2．S为三角形ABC所在平面外一点，SA⊥平面ABC，平面SAB⊥平面SBC。求证：ABBC⊥。SCBAD证明：过A点作ADSB⊥于D点.∵平面SAB⊥平面SBC,∴AD⊥平面SBC，∴ADBC.⊥又∵SA⊥平面ABC，∴SABC.⊥AD∩SA=ABC∴⊥平面SAB.BC∴AB.⊥新知探究练习1：如图，以正方形ABCD的对角线AC为折痕，使△ADC和△ABC折成相垂直的两个面，求BD与平面ABC所成的角。ABCDDABCOO折成新知探究2.如图，平面AED⊥平面ABCD，△AED是等边三角形，四边形ABCD是矩形，（1）求证：EACD⊥MDECAB（2）若AD＝1，AB＝，求EC与平面ABCD所成的角。2新知探究2(2012·北京模拟)如图，正方形ADEF与梯形ABCD所在的平面互相垂直，ADCD⊥，ABCD∥，AB=AD=2，CD=4，M为CE的中点.(1)求证：BM∥平面ADEF；(2)求证：平面BDE⊥平面BEC.新知探究证明：(1)取DE中点N，连接MN，AN.在△EDC中，M，N分别为EC，ED的中点，所以MN//CD，且MN=CD.由已知AB//CD，AB=CD，所以MN//AB,且MN=AB,所以四边形ABMN为平行四边形.所以BM//AN.又因为AN平面ADEF，且BM平面ADEF，所以BM//平面ADEF.1212新知探究1212(2)因为四边形ADEF为正方形，所以EDAD⊥，又因为平面ADEF⊥平面ABCD，且平面ADEF∩平面ABCD=AD.又因为EDB平面ADEF，所以ED⊥平面ABCD.所以EDBC.⊥新知探究在直角梯形ABCD中，AB=AD=2，CD=4，可得BC=，在△BCD中，BD=BC=，CD=4，所以BCBD⊥，BD∩ED=D,所以BC⊥平面BDE，又因为BC平面BCE，所以平面BDE⊥平面BEC.2222新知探究2222（4）已知面面垂直易找面的垂线，且在某一个平面内（5）解题过程中应注意充分领悟、应用（3）证明面面垂直要从寻找面的垂线入手（2）理解面面垂直的判定与性质都要依赖面面垂直的定义（1）定义面面垂直是在建立在二面角的定义的基础上的线面垂直面面垂直线线垂直面面垂直线面垂直线线垂直总结提炼αβaAB线线垂直线面垂直线线平行面面平行面面垂直垂直、平行关系小结：总结提炼2.面面垂直的性质推论：1.平面与平面垂直的性质定理：面面垂直线面垂直αβγlαβAbalβαPaalaα∥DCAB总结提炼al感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明讲解人：办公资源时间：2020.6.1MENTALHEALTHCOUNSELINGPPT感谢你的聆听第2章关系点、直线、平面之间的位置关系人教版高中数学必修二