《椭圆的简单几何性质》人教版高中数学选修2-1PPT课件（第1课时）.pptx

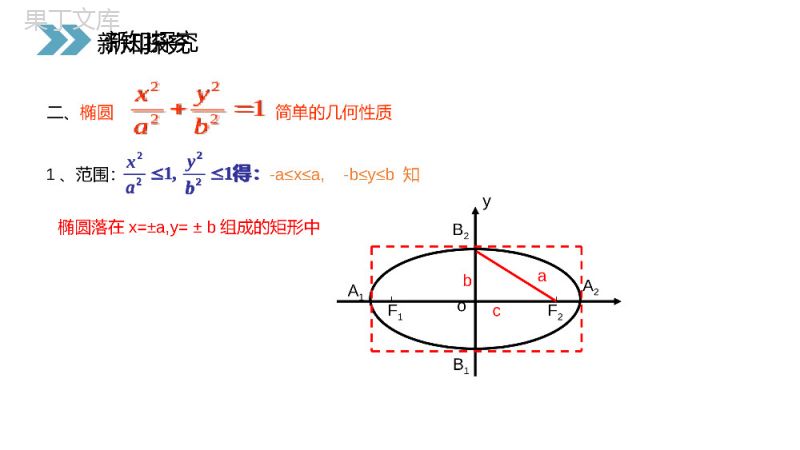
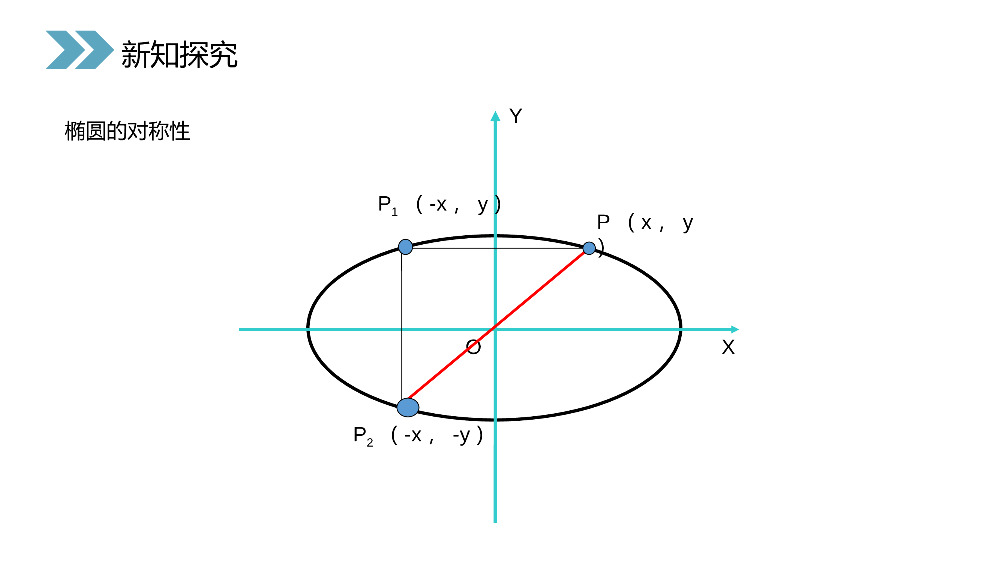
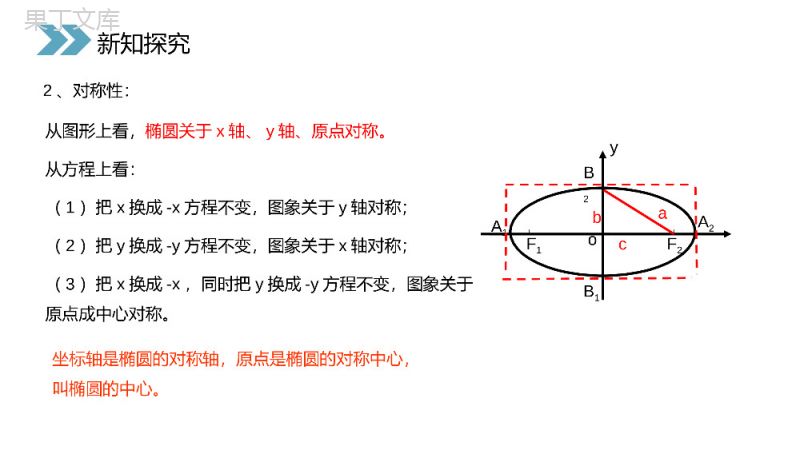
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-12.2.2椭圆的简单几何性质第一课时第2章圆锥曲线与方程人教版高中数学选修2-11.椭圆的定义:到两定点F1、F2的距离之和为常数（大于F1F2）的动点的轨迹叫做椭圆。2.椭圆的标准方程是：3.椭圆中a,b,c的关系是:a2=b2+c2)2(22121FFaaPFPF当焦点在X轴上时当焦点在Y轴上时)0(12222babyax)0(12222babxay课前导入)2(22121FFaaPFPF)0(12222babyax)0(12222babxay二、椭圆简单的几何性质-a≤x≤a,-b≤y≤b知,122ax得：122byoyB2B1A1A2F1F2cab1、范围：椭圆落在x=±a,y=±b组成的矩形中新知探究新知探究12222byax,122ax得：122by椭圆的对称性YXOP（x，y）P1（-x，y）P2（-x，-y）新知探究2、对称性：oyB2B1A1A2F1F2cab从图形上看，椭圆关于x轴、y轴、原点对称。从方程上看：（1）把x换成-x方程不变，图象关于y轴对称；（2）把y换成-y方程不变，图象关于x轴对称；（3）把x换成-x，同时把y换成-y方程不变，图象关于原点成中心对称。坐标轴是椭圆的对称轴，原点是椭圆的对称中心，叫椭圆的中心。新知探究3、椭圆的顶点（截距）)0(12222babyax令x=0，得y=？，说明椭圆与y轴的交点？令y=0，得x=？说明椭圆与x轴的交点？顶点：椭圆与它的对称轴的四个交点，叫做椭圆的顶点。长轴、短轴：线段A1A2、B1B2分别叫做椭圆的长轴和短轴。a、b分别叫做椭圆的长半轴长和短半轴长。oyB2B1A1A2F1F2cab(0,b)(a，0)(0,-b)(-a，0)新知探究)0(12222babyax123-1-2-3-44y123-1-2-3-44y12345-1-5-2-3-4x12345-1-5-2-3-4x根据前面所学有关知识画出下列图形1162522yx142522yx（1）（2）A1B1A2B2B2A2B1A1新知探究1162522yx142522yx4、椭圆的离心率e(刻画椭圆扁平程度的量)ace离心率：椭圆的焦距与长轴长的比：叫做椭圆的离心率。[1]离心率的取值范围：[2]离心率对椭圆形状的影响：0bceaa2=b2+c2新知探究22221(0)xyababcea标准方程范围对称性顶点坐标焦点坐标半轴长离心率a、b、c的关系22221(0)xyabba22221(0)xyababx≤a,y≤b关于x轴、y轴成轴对称；关于原点成中心对称(a,0)、(-a,0)、(0,b)、(0,-b)(c,0)、(-c,0)长半轴长为a,短半轴长为b.a>bceaa2=b2+c2x≤b,y≤a同前(b,0)、(-b,0)、(0,a)、(0,-a)(0,c)、(0,-c)同前同前同前新知探究22221(0)xyabba22221(0)xyababcea它的长轴长是：。短轴长是：。焦距是：。离心率等于：。焦点坐标是：。顶点坐标是：。外切矩形的面积等于：。例1已知椭圆方程为9x2+25y2=225,451068(5,0),(0,3)(0,4)60解题的关键：192522yx2、确定焦点的位置和长轴的位置题型一：利用椭圆方程，研究其几何性质1、将椭圆方程转化为标准方程明确a、b新知探究45(5,0),(0,3)(0,4)192522yx已知椭圆方程为6x2+y2=6它的长轴长是：。短轴长是：。焦距是：.离心率等于：。焦点坐标是：。顶点坐标是：。外切矩形的面积等于：。262)5,0(52630(0,6)(1,0)4616122yx其标准方程是51622bacba则新知探究练习1.62)5,0(52630(0,6)(1,0)4616122yx其标准方程是51622bacba则练习求下列椭圆的长轴长、短轴长、焦点坐标、顶点坐标和离心率。（1）x2+9y2=81(2)25x2+9y2=225(3)16x2+y2=25(4)4x2+5y2=122(1)1819xy22(3)1252516xy22(2)1925xy22(4)11145xy新知探究22(1)1819xy22(3)1252516xy22(2)1925xy22(4)11145xy练习：已知椭圆的离心率求m的值及椭圆的长轴和短轴的长、焦点坐标、顶点坐标。22(3)(0)xmymm3,2e2213xymmm椭圆：222(2),,33mmmambcmm22334mem1m22a长轴长21b短轴长3,0)2焦点坐标(11,0),(0,)2顶点坐标(新知探究22(3)(0)xmymm3,2e2213xymmm椭圆：222(2),,33mmmambcmm22334mem1m22a长轴长21b短轴长3,0)2焦点坐标(11,0),(0,)2顶点坐标(例2求适合下列条件的椭圆的标准方程⑴经过点P(－3,0)、Q(0,－2)；⑵长轴长等于20，离心率3/5。⑶一焦点将长轴分成２:１的两部分,且经过点32,4P22194xy所求椭圆方程为：解：⑴方法一：设方程为mx2＋ny2＝1（m＞0，n＞0，m≠n），注：待定系数法求椭圆标准方程的步骤：⑴定位；⑵定量题型二：利用椭圆的几何性质求标准方程将点的坐标方程，求出m＝1/9,n＝1/4。新知探究32,4P22194xy所求椭圆方程为：例2求适合下列条件的椭圆的标准方程⑴经过点P(－3,0)、Q(0,－2)；⑵长轴长等于20，离心率3/5。⑶一焦点将长轴分成２:１的两部分,且经过点32,4P22194xy解：(1)方法二：利用椭圆的几何性质注：待定系数法求椭圆标准方程的步骤：⑴定位；⑵定量题型二：利用椭圆的几何性质求标准方程以坐标轴为对称轴的椭圆与坐标轴的交点就是椭圆的顶点，于是焦点在x轴上，且点P、Q分别是椭圆长轴与短轴的一个端点，故a＝3，b＝2，所以椭圆的标准方程为新知探究32,4P22194xy例2求适合下列条件的椭圆的标准方程⑴经过点P(－3,0)、Q(0,－2)；⑵长轴长等于20，离心率3/5。⑶一焦点将长轴分成２:１的两部分,且经过点32,4P3220,5caea：解(2)注：待定系数法求椭圆标准方程的步骤：⑴定位；⑵定量2222111006410064xyyx椭圆方程为：或题型二：利用椭圆的几何性质求标准方程10,6ac8.b新知探究32,4P3220,5caea：解(2)2222111006410064xyyx椭圆方程为：或10,6ac8.b例2求适合下列条件的椭圆的标准方程⑴经过点P(－3,0)、Q(0,－2)；⑵长轴长等于20，离心率3/5。⑶一焦点将长轴分成２:１的两部分,且经过点32,4P一焦点将长轴分成２：１解:(3)的两部分222211145290363249xyyx椭圆方程为：或题型二：利用椭圆的几何性质求标准方程():()2:1acac3ac228bc22222222119889xyxycccc椭圆方程可设为：或22222222(32)4(32)4119889cccc或32,4P椭圆过，22145436cc或新知探究32,4P一焦点将长轴分成２：１解:(3)的两部分222211145290363249xyyx椭圆方程为：或():()2:1acac3ac228bc22222222119889xyxycccc椭圆方程可设为：或22222222(32)4(32)4119889cccc或32,4P椭圆过，22145436cc或练习：已知椭圆的中心在原点，焦点在坐标轴上，长轴是短轴的三倍，且椭圆经过点P（3，0），求椭圆的方程。2222119981xxyy或分类讨论的数学思想232ab3ab3,1ab39ba或，课堂练习2222119981xxyy或232ab3ab3,1ab39ba或，1.根据下列条件，求椭圆的标准方程。①长轴长和短轴长分别为8和6，焦点在x轴上②长轴和短轴分别在y轴，x轴上，经过P(-2,0)，Q(0,-3)两点.③一焦点坐标为（－3，0）一顶点坐标为（0，5）④两顶点坐标为（0，±6），且经过点（5，4）⑤焦距是12，离心率是0.6，焦点在x轴上。22169xy①+=12294yx②+=1223425xy③+=12210064xy⑤+=1224536xy④+=1课堂练习22169xy①+=12294yx②+=1223425xy③+=12210064xy⑤+=1224536xy④+=12.已知椭圆的一个焦点为F（6，0）点B，C是短轴的两端点，△FBC是等边三角形，求这个椭圆的标准方程。6c2ab362a43,23ab2214812xy椭圆方程为：课堂练习6c2ab362a43,23ab2214812xy椭圆方程为：本节课我们学习了椭圆的几个简单几何性质：范围、对称性、顶点坐标、离心率等概念及其几何意义。了解了研究椭圆的几个基本量a，b，c，e及顶点、焦点、对称中心及其相互之间的关系，这对我们解决椭圆中的相关问题有很大的帮助，给我们以后学习圆锥曲线其他的两种曲线扎实了基础。在解析几何的学习中，我们更多的是从方程的形式这个角度来挖掘题目中的隐含条件，需要我们认识并熟练掌握数与形的联系。在本节课中，我们运用了几何性质，待定系数法来求解椭圆方程，在解题过程中，准确体现了函数与方程以及分类讨论的数学思想。小结感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-1感谢你的聆听第2章圆锥曲线与方程人教版高中数学选修2-1