等腰三角形的性质第1课时,等腰三角形的性质说课稿

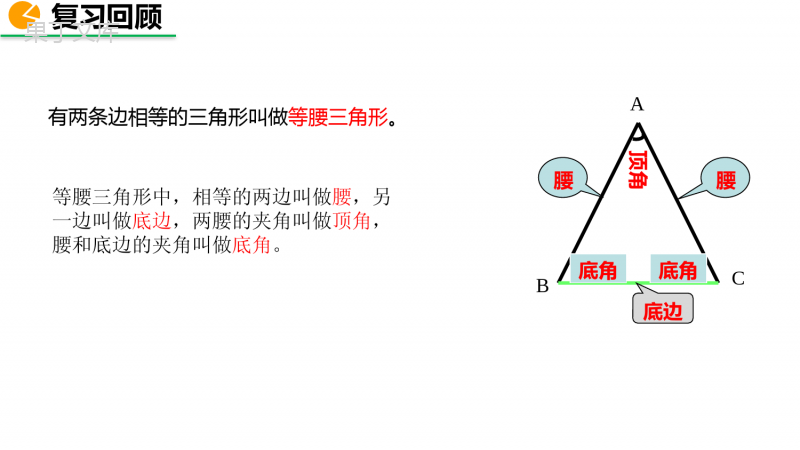
13.3等腰三角形第1课时生活中的等腰三角形钝角三角形直角三角形锐角三角形腰腰顶角底角底角底边复习回顾有两条边相等的三角形叫做等腰三角形。等腰三角形中，相等的两边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。ABC1.探索并掌握等腰三角形的两个性质．2.会运用等腰三角形的概念和性质解决有关问题.学习目标把一张长方形的纸按图中的虚线对折，并剪去阴影部分，再把它展开，得到的△ABC有什么特点？探究新知做一做ABCAB=AC等腰三角形探究新知△ABC是轴对称图形吗？它的对称轴是什么？ACDB折痕所在的直线是它的对称轴.等腰三角形是轴对称图形.探究新知想一想把剪出的等腰三角形ABC沿折痕对折，找出其中重合的线段和角.重合的线段重合的角ACBDAB与ACBD与CDAD与AD∠B与∠C.∠BAD与∠CAD∠ADB与∠ADC由这些重合的角，你能发现等腰三角形的性质吗？说一说你的猜想.探究新知想一想概括归纳等腰三角形的性质性质1：等腰三角形的两个底角相等。性质2：等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合。ABC已知：△ABC中，AB=AC,求证：∠B=∠C。思考：如何构造两个全等的三角形？猜想:等腰三角形的两个底角相等.如何证明两个角相等呢？可以运用全等三角形的性质“对应角相等”来证.探究新知已知：如图，在△ABC中，AB=AC.求证：∠B=∠C.ABCD证明：作底边的中线AD，则BD=CD.AB=AC(已知)，BD=CD(已作)，AD=AD(公共边)，∴△BAD≌△CAD(SSS).∴∠B=∠C(全等三角形的对应角相等).在△BAD和△CAD中方法一：作底边上的中线.还有其他的证法吗？探究新知已知：如图，在△ABC中，AB=AC.求证：∠B=∠C.ABCD证明：作顶角的平分线AD，则∠BAD=∠CAD.AB=AC(已知),∠BAD=∠CAD(已作),AD=AD(公共边),∴△BAD≌△CAD(SAS).∴∠B=∠C(全等三角形的对应角相等).方法二：作顶角的平分线在△BAD和△CAD中探究新知由△BAD≌△CAD，除了可以得到∠B=∠C之外，你还可以得到哪些相等的线段和相等的角？和你的同伴交流一下，看看你有什么新的发现？解：∵△BAD≌△CAD，由全等三角形的性质易得BD=CD,∠ADB=∠ADC，∠BAD=∠CAD.又∵∠ADB+∠ADC=180°，∴∠ADB=∠ADC=90°，即AD是等腰△ABC底边BC上的中线、顶角∠BAC的角平分线、底边BC上的高线.ABCD探究新知想一想性质1:等腰三角形的两个底角相等(等边对等角).ACB应用格式：在△ABC中,∵AB=AC(已知),∴∠B=∠C(等边对等角).性质2:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一）.即：等腰三角形顶角平分线底边上的高线底边上的中线具备其中一条另外两条成立探究新知归纳总结ACBD12∵AB=AC,1=2(∠∠已知)，∴BD=CD,AD⊥BC（等腰三角形三线合一）∵AB=AC,BD=CD(已知)，∴∠1=2,∠AD⊥BC（等腰三角形三线合一）∵AB=AC,AD⊥BC(已知)，∴BD=CD,1=2∠∠（等腰三角形三线合一）应用格式：在△ABC中,探究新知ABCD例1如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求△ABC各角的度数.分析：（1）出图中有几个等腰三角形？（2）找出图中所有相等的角；∠A=∠ABD,∠C=∠BDC=∠ABC△ABC,△ABD,△BCD例题讲解ABCDx°⌒2x°⌒2x°⌒⌒2x°（3）观察∠BDC与∠A、∠ABD的关系，∠ABC、∠C呢？∠BDC=∠A+∠ABD=2∠A=2∠ABD,∠ABC=∠BDC=2∠A,∠C=∠BDC=2∠A.（4）设∠A=x°,请把△ABC的内角和用含x的式子表示出来.∵∠A+∠ABC+∠C=180°，∴x°+2x°+2x°=180°,例题讲解ABCD解：∵AB=AC，BD=BC=AD，∴∠ABC=C=BDC∠∠，∠A=ABD∠.设∠A=x°,则∠BDC=∠A+∠ABD=2x°,从而∠ABC=∠C=∠BDC=2x°,于是在△ABC中，有∠A+∠ABC+∠C=x°+2x°+2x°=180°，解得x=36，在△ABC中，∠A=36°∠ABC=∠C=72°.x°⌒2x°⌒2x°⌒⌒2x°例题讲解（1）等腰三角形的一个底角是75°，它的另外两个角为_____________________;课堂练习（2）等腰三角形的一个角是36°，它的另外两个角为______________________;（3）等腰三角形的一个角是120°，它的另外两个角为______________________。75°，30°30°，30°36°，108°或72°，72°如图，在△ABC中，AB=AC，AD和BE是高，它们相交于点H，且AE=BE，求证：AH=2BD.课堂练习证明：∵AB=AC中，AD是高，∴BC=2BD∵AD，BE是高，∴∠ADC=90°，∠AEH=∠ADC=90°∴∠HAE+∠C=90°，∠CBE+∠C=90°∴∠HAE=∠CBE在△AEH和△BEC中，∴△AEH≌△BEC（ASA），∴AH=BC又∵BC=2BD，∴AH=2BADC∠=AEH∠BE=AECBE∠=HAE∠ADC∠=AEH∠BE=AECBE∠=HAE∠等腰三角形的性质等边对等角三线合一注意是指同一个三角形中.注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上的高和中线与底角的平分线不具有这一性质.易错点拨（1）求等腰三角形角的度数时，如果没有明确是底角还是顶角必须分类讨论.（2）等腰三角形“三线合一”定理，角平分线指的是“顶角平分线”.课堂小结2.等腰三角形的一个底角为50°，则它的顶角的度数为_____.课后作业3.如图，AD，CE分别是△ABC的中线和角平分线．若AB=AC，∠CAD=20°，则∠ACE的度数是_______.1.画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高，看看它们是否重合？并思考为什么？