中考专题--构造直角三角形解根号2、根号3倍的线段数量关系

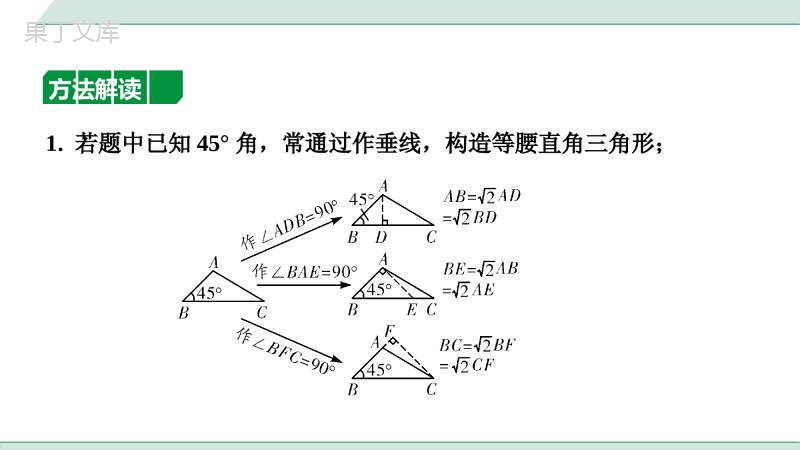
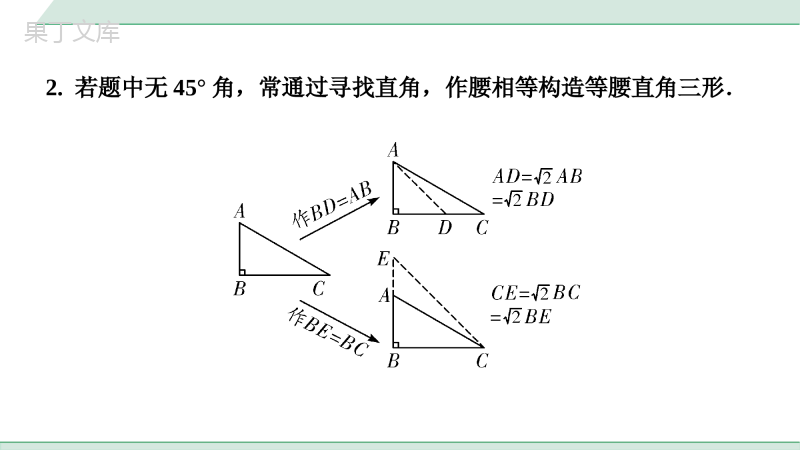
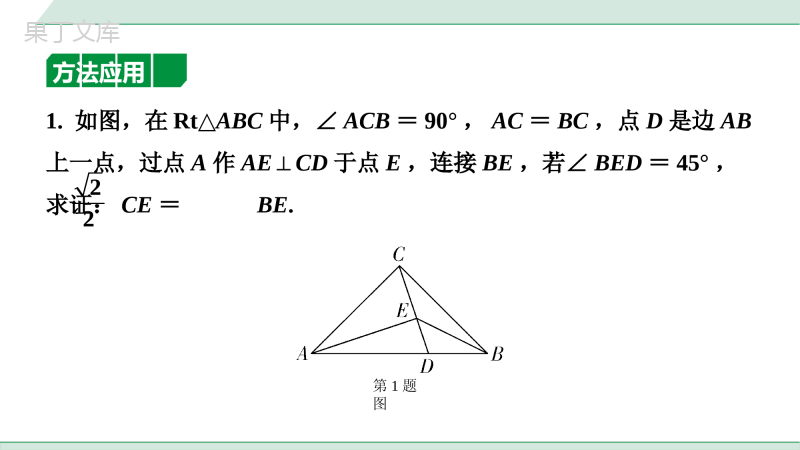
类型一构造含45°角的直角三角形解倍的线段数量关系2中考专题构造直角三角形解、倍的线段数量关系23223满分技法方法解读1.若题中已知45°角，常通过作垂线，构造等腰直角三角形；2.若题中无45°角，常通过寻找直角，作腰相等构造等腰直角三形．方法应用1.如图，在Rt△ABC中，∠ACB＝90°，AC＝BC，点D是边AB上一点，过点A作AE⊥CD于点E，连接BE，若∠BED＝45°，求证：CE＝BE.22第1题图22第1题图【证法一】以BE为斜边构造含45°角的直角三角形．证明：如解图①，过点B作BF⊥ED，交ED延长线于点F，∴∠EFB＝90°，∵∠BED＝45°，∴BF＝BE·sin45°＝BE，∵∠CAE＋∠ACE＝90°，∠FCB＋∠ACE＝90°，∴∠CAE＝∠FCB，22F22∵AE⊥CD，∴∠AEC＝∠CFB＝90°，在△AEC和△CFB中，∴△AEC≌△CFB(AAS)，∴CE＝FB，∴CE＝BE.,AECCFBCAEBCFACCB22第1题图F,AECCFBCAEBCFACCB22第1题图【证法二】以CE为直角边构造含45°角的直角三角形．证明：如解图②，在线段AE上截取EF＝EC，连接CF，F∵AE⊥CD，∴∠EFC＝∠ECF＝45°，∴CE＝CF·sin45°＝CF，∵∠CFE＝45°，∠BED＝45°，∴∠CFA＝∠BEC＝135°，∵AE⊥CD，2222∴∠AEC＝∠ACB＝90°，∴∠CAF＋∠ACE＝∠BCE＋∠ACE＝90°，∴∠CAF＝∠BCE，在△CAF与△BCE中，∴△CAF≌△BCE(AAS)，∴CF＝BE，∴CE＝BE.,CFABECCAFBCEACCB22第1题图F,CFABECCAFBCEACCB22类型二构造含30°或60°角的直角三角形解倍的线段数量关系方法解读1.若题中已知30°角，常通过作垂线构造含30°角的直角三角形；332.若选中无30°角，常通过寻找直角三角形中的边的关系，截长补短构造含30°角的直角三角形．方法应用2.如图，在Rt△ABC中，∠ABC＝90°，∠A＝30°，点D，E，F分别在AB，BC，AC上，且DE＝EF，∠DEF＝90°，试猜想CF与BE之间的数量关系，并证明．第2题图第2题图【证法一】以CF为斜边构造含30°角的直角三角形．证法一：如解图①，过点F作FG⊥BC于点G，∵∠ABC＝90°，∠A＝30°，∴∠C＝60°，∠BDE＋∠DEB＝90°，∵∠FGE＝∠FGC＝90°，∴∠GFC＝30°，∴FG＝CF·cos∠GFC＝CF，∵∠DEF＝90°，∴∠GEF＋∠DEB＝90°，32解：BE＝CF32G3232∴∠BDE＝∠GEF，在△DBE与△EGF中，∴△DBE≌△EGF(AAS)，∴BE＝FG，∴BE＝CF.32,BEGFBDEGEFDEEF第2题图G32,BEGFBDEGEFDEEF第2题图【证法二】以BE为直角边构造含30°角的直角三角形．证明：如解图②，在AB的延长线上取点G，连接EG，使得∠G＝∠C.∵∠ABC＝90°，∠A＝30°，∴∠C＝60°，∴∠G＝∠C＝60°，∠EBG＝∠ABC＝90°，∴在Rt△BEG中，BE＝EG·sinG＝EG，在Rt△BDE中，∠BDE＋∠BED＝90°，32G32∴∠CEF＋∠BED＝90°，∴∠EDG＝∠BDE＝∠CEF，在△DEG与△EFC中，∴△DEG≌△EFC(AAS)，∴EG＝CF，∴BE＝EG＝CF.,BEGFBDEGEFDEEF3232第2题图G,BEGFBDEGEFDEEF3232