三角形的外角,三角形的外角等于与它不相邻的两个内角的和

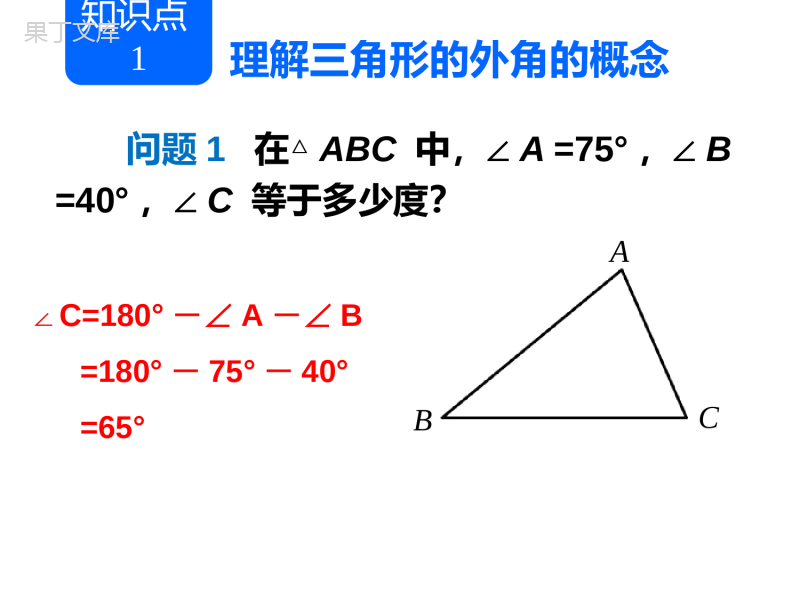
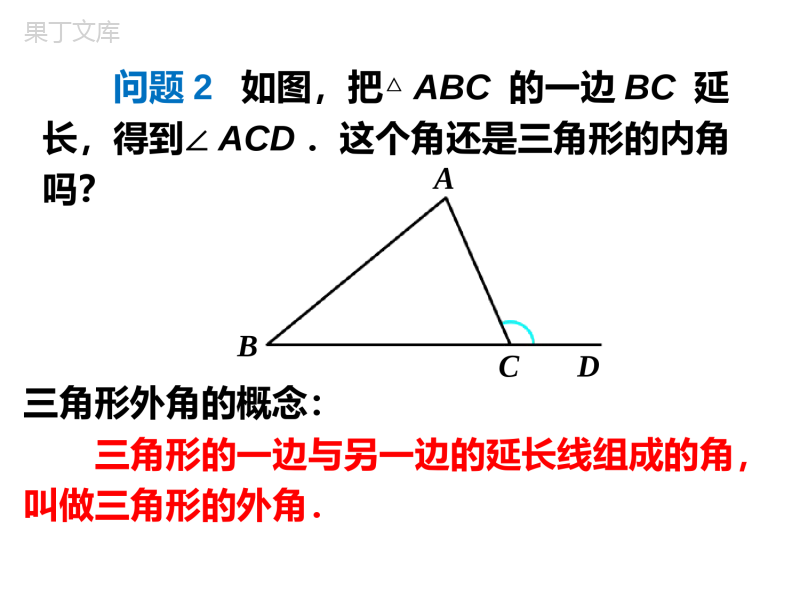
11.2.2三角形的外角1．能准确地判断一个三角形的外角.2．能叙述和证明三角形的外角的性质.3．能利用三角形的外角性质解决实际问题.学习目标导学案反馈存在的问题：1、外角的证明2、外角和的使用理解三角形的外角的概念知识点1问题1在△ABC中，∠A=75°，∠B=40°，∠C等于多少度？ABC∠C=180°－∠A－∠B=180°－75°－40°=65°ABCD问题2如图，把△ABC的一边BC延长，得到∠ACD．这个角还是三角形的内角吗？三角形外角的概念：三角形的一边与另一边的延长线组成的角，叫做三角形的外角．ABCD∠ACD（外角）+∠ACB（相邻的内角）=180°．问题3如图，∠ACD与∠ACB的位置是怎样的？∠ACD与∠ACB有什么数量关系？探索与证明三角形的外角的性质知识点2ABCD如图，∵∠ACD+∠ACB=180°，∠A+∠B+∠ACB=180°，∴∠ACD=∠A+∠B．问题4如图，∠ACD与∠A，∠B的大小有什么关系？你能证明你的结论吗？三角形内角和定理的推论：三角形的一个外角等于与它不相邻的两个内角的和。三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角的和。∠C∠3∠DAC∠4练习1如图，口答：（1）∠1=+；（2）∠2=+．BACD1234练习2如图，说出图形中∠1的度数．图中∠1的度数依次为：90°，85°，95°，45°．（1）（2）（3）（4）30°60°135°60°145°50°130°15°1练习3如图，一个三角形有______个外角.每个顶点处有______个外角，这两个外角是____________.62对顶角百家争鸣，百花齐放——成长与精彩属于我们具体要求：重点探究：如何正确的利用三角形外角的性质去解决问题展示要求:(1)书写认真、步骤规范，用好双色笔。(2)总结题目的规律、方法，注重多角度考虑问题。(3)先组内讨论，再组间学习；展示题目展示小组巩固提升1、25巩固提升33迁移提升1要求（1）书面展示要分层次，书写要认真、规范。（2）非展示同学巩固基础知识、整理落实学案，做好拓展。把典型的题目整理到典型题集上，不浪费一分钟，小组长做好安排和检查。1.面向同学，声音洪亮，语言精炼，自然大方；2.点评时注重对题目思路和方法的分析，点明注意事项，并总结方法和规律；3.其他同学要求极度专注，积极质疑、追问、解答。点评题目点评小组巩固提升1、26巩固提升34迁移提升2运用三角形的外角的性质知识点3例如图，∠BAE，∠CBF，∠ACD是△ABC的三个外角，它们的和是多少？ABFCDE123解法一：∵∠BAE=2+3∠∠，∠CBF=1+3∠∠，∠ACD=1+2∠∠，∴∠BAE+∠CBF+∠ACD=(2+3)+(1+3)+∠∠∠∠(1+2)∠∠=2（∠1+2+3∠∠）．ABFCDE123∵∠1+2+3=180°∠∠，∴∠BAE+∠CBF+∠ACD=2×180°=360°.ABFCDE123解法二：∵∠1+∠BAE=180°，∠2+∠CBF=180°，∠3+∠ACD=180°，∴∠1+2+3+∠∠∠BAE+∠CBF+∠ACD=540°．∵∠1+2+3=180°∠∠，∴∠BAE+∠CBF+∠ACD=540°-180°=360°.ABDC练习4如图，D是△ABC的边BC上一点，∠B=∠BAD，∠ADC=80°，∠BAC=70°.求：（1）∠B的度数；（2）∠C的度数．解：（1）∠ADC=∠B+∠BAD=2∠B∠B=40°（2）∠C+∠B+∠BAC=180°∠C=180°-70°-40°=70°随堂演练1.如图，∠1=_______.2.如图，AB∥CD，∠A=40°，∠D=45°，则∠1=_______.110°85°第1题图第2题图基础巩固3.如图，已知∠1=100°，∠2=140°，那么∠3=_______.120°第3题图4.已知三角形的三个外角的度数比为234∶∶，则它的最大内角度数为（）A.90°B.110°C.100°D.120°C综合应用ABCD如图，∵∠ACD+∠ACB=180°，∠A+∠B+∠ACB=180°，∴∠ACD=∠A+∠B．三角形内角和定理的推论：三角形的一个外角等于与它不相邻的两个内角的和．课堂小结