求解二元一次方程组(第2课时)-2022-2023学年八年级数学上册同步教材教学精品课件(北师大版)

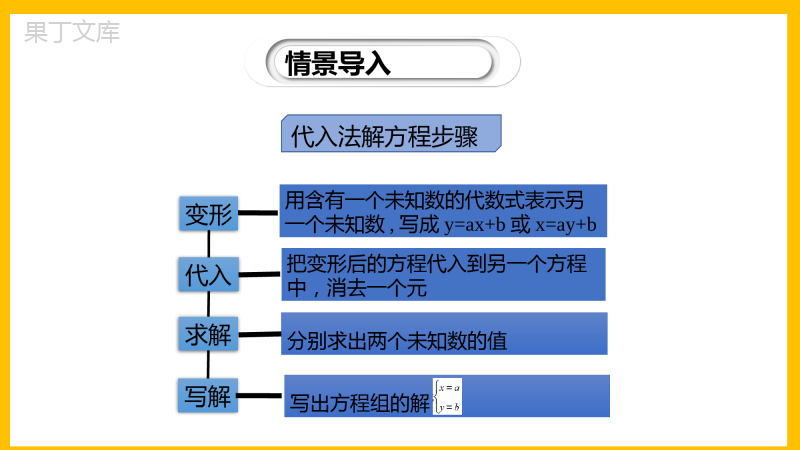
第五章二元一次方程组5.2.2求解二元一次方程组（第2课时）北师版数学八年级上册学习目标1、会用加减消元法解二元一次方程组.2、了解“消元”思想，初步体会数学研究中“化未知为已知”的化归思想.情景导入基本思路消元:二元一元二元一次方程组“元”“次”，指整式方程情景导入写解求解代入把变形后的方程代入到另一个方程中，消去一个元分别求出两个未知数的值变形用含有一个未知数的代数式表示另一个未知数,写成y=ax+b或x=ay+b代入法解方程步骤写出方程组的解探索新知用加减法解二元一次方程组一3x+5y=21①2x–5y=-11②同学们，你能用前面学过的代入法解下面的二元一次方程组吗?思考：习惯用系数最小的未知数进行变形，那这个方程组用哪个未知数表示另一个未知数？把②变形得：③③代入①，不就消去x了！511,2yx-=5y511,2yx-=探索新知把②变形得1125xy可以直接代入①呀！3x+5y＝21①3x+(2x+11)＝213x+5y=21①2x–5y=-11②同学们，你能用前面学过的代入法解下面的二元一次方程组吗?1125xy探索新知3x+5y=21①2x–5y=-11②除了学过的代入消元法下面的二元一次方程组，有没有其它的方法解方程组？5y和－5y互为相反数……①左边+②左边=①右边+②右边等式的基本性质探索新知3x+5y=21①2x–5y=-11②3x+5y=21①2x-5y=-11②010=5x10=++利用算式方式分析：5x解：由①+②，得:将x=2代入①，得：6+5y=21y=3∴原方程组的解是x=2y=35x=10x=2方程组标准书写过程：你学会了吗？探索新知像上面这种解二元一次方程组的方法,叫做加减消元法,简称加减法.当方程组中两个方程的某个未知数的系数互为相反数或相等时,可以把方程的两边分别相加(系数互为相反数)或相减(系数相等)来消去这个未知数,得到一个一元一次方程,进而求得二元一次方程组的解.总结归纳特点基本思路加减消元：二元一同一个未知数的系数相同或互为相反数.总结归纳探索新知主要步骤“五步法”回代求解加减两个方程的左右两边分别相加或相减，消去一个元；分别求出两个未知数的值；把求得的未知数的值代入原方程组中求另一值.加减法解二元一次方程组写解写出原方程组的解.变形通过变形使方程组中两个方程的某一个未知数的系数绝对值相等．探索新知例1解方程组2x-5y=7①2x+3y=-1②1.这个方程组中,哪个未知数的系数有特点?2.采用什么办法消去未知数系数?方程①、②中未知数x的系数相等，可以利用两个方程相减消去未知数x.探索新知2x+3y=-1②2x-5y=7①8y-8=0-8=-+利用算式方式分析：8y解：②-①，得8y=-8,y=-1.将y=-1代入①,得2x+5=7,x=1.所以方程组的解是x=1,y=-1.总结：同一未知数的系数时，把两个方程的两边分别！相等相减探索新知例2.解方程组2x+3y=12①3x+4y=17②这个方程组中,未知数的系数既不相同也不互为相反数,怎么解？能否使两个方程中x(或y)的系数相等(或相反)呢?找系数的最小公倍数探索新知6x+9y=36①×36x+8y=34×2②y2=02=-+利用算式方式分析：y解：由①×3，得6x+9y=36.③由②×2，得6x+8y=34.④③-④，得y=2.将y=2代入①,得x=3.∴方程组的解是x=3,y=2.总结：同一未知数的系数时，利用等式的性质，使得未知数的系数不相等也不互为相反数相等或互为相反数探索新知总结归纳加减消元法同一未知数系数绝对值相同系数相同相减系数互为相反数相加同一未知数系数绝对值不相同找系数的最小公倍数使得未知数的系数相等或互为相反数探索新知例3：已知,则a+b等于_____.82342baba3①②分析：方法一，直接解方程组，求出a与b的值，然后就可以求出a+b.方法二：+得4a+4b=12，a+b=3.【方法总结】解题的关键是观察两个方程相同未知数的系数关系，利用加减消元法求解.82342baba当堂检测1．方程组3x＋2y＝5，①－2x＋2y＝－6，②用①－②得()A．x＝－1B．x＝11C．5x＝11D．5x＝－1C2．若a＋b＝3，a－b＝7，则ab等于()A．－10B．－40C．10D．40A1．方程组3x＋2y＝5，①－2x＋2y＝－6，②用①－②得()A．x＝－1B．x＝11C．5x＝11D．5x＝－12．若a＋b＝3，a－b＝7，则ab等于()A．－10B．－40C．10D．40当堂检测3．已知x＝2，y＝1是二元一次方程组ax＋by＝7，ax－by＝1的解，则a－b的值为()A．－1B．1C．2D．3A3．已知x＝2，y＝1是二元一次方程组ax＋by＝7，ax－by＝1的解，则a－b的值为()A．－1B．1C．2D．3当堂检测4．解方程组3x－2y＝1，①4x＋2y＝6.②最简捷的方法是_____________得__________，把_________代入②得_________，所以原方程组的解为______________．①＋②x＝1x＝1y＝1x＝1y＝15.解方程组4x－3y＝2，①4x＋3y＝1.②既可用___________消去未知数______；也可用____________来消去未知数_______．①－②x①＋②y4．解方程组3x－2y＝1，①4x＋2y＝6.②最简捷的方法是_____________得__________，把_________代入②得_________，所以原方程组的解为______________．x＝1y＝15.解方程组4x－3y＝2，①4x＋3y＝1.②既可用___________消去未知数______；也可用____________来消去未知数_______．当堂检测6．用加减消元法解方程组：x+3y=122x-3y=66x+7y=-196x-5y=17当堂检测解：(1)x+3y=12①2x-3y=6②①＋②，得3x＝18，解得x＝6.把x＝6代入方程①，得6＋3y＝12，解得y＝2.所以原方程组的解为x=6y=2当堂检测解：(2)6x+7y=-19①6x-5y=17②①-②，得12x＝-36，解得x＝-3.把x＝-3代入方程①，得-18＋7y＝-19，解得y＝2/7.所以原方程组的解为x=-3y=2/7当堂检测7．老师布置了一个探究活动作业：仅用一驾天平和一个10克的砝码测量壹元硬币和伍角硬币的质量．(注：同种类的每枚硬币质量相同)聪明的小明同学找来足够多的壹元和伍角的硬币，经过探究得到以下两个探究记录：当堂检测请你用所学的数学知识计算出一枚壹元硬币多少克，一枚伍角硬币多少克？解：设一枚壹元硬币x克，一枚伍角硬币y克，依题意得5x＋10＝10y，15x＝20y＋10，解得x＝6，y＝4.答：一枚壹元硬币6克，一枚伍角硬币4克解：设一枚壹元硬币x克，一枚伍角硬币y克，依题意得5x＋10＝10y，15x＝20y＋10，解得x＝6，y＝4.答：一枚壹元硬币6克，一枚伍角硬币4克加减消元法解方程组基本思路是：加减消元二元一元同一未知数的系数互为相反数时同一未知数的系数相等时同一未知数的系数既不相等也不互为相反数时加法减法等式基本性质