应用一元一次方程—水箱变高了-2022-2023学年七年级数学上册教材配套教学课件(北师大版)

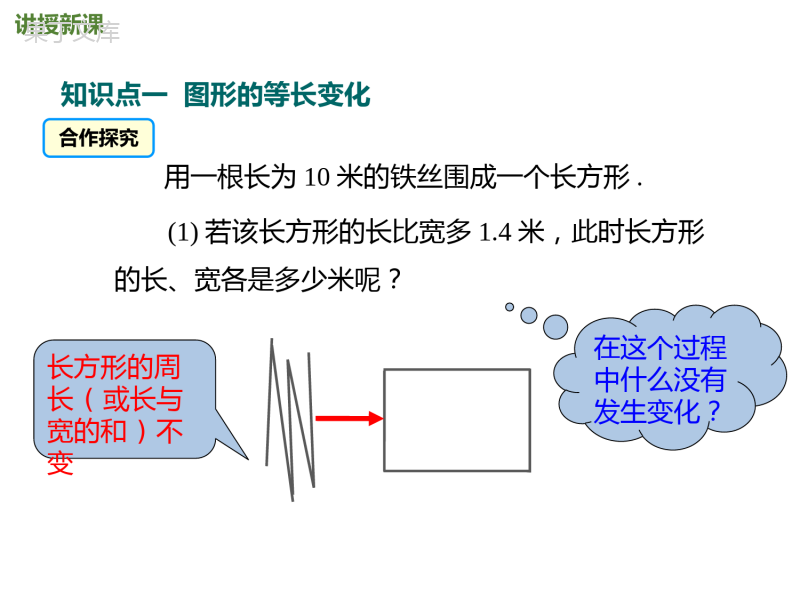
第五章一元一次方程5.3应用一元一次方程—水箱变高了北师大版七年级上册新课导入讲授新课当堂检测课堂小结学习目标1、学会分析题目复杂关系的数量关系和等量关系，列出一元一次方程；2、学会用一元一次方程解决简单的图形问题，注意设未知数，然后用未知数表示其他的量，构建一元一次方程；导入新课从一个水杯向另一个水杯倒水想一想：右边的水杯水量有变化吗？讲授新课知识点一图形的等长变化合作探究(1)若该长方形的长比宽多1.4米，此时长方形的长、宽各是多少米呢？在这个过程中什么没有发生变化？长方形的周长(或长与宽的和)不变用一根长为10米的铁丝围成一个长方形.xm(x+1.4)m等量关系：（长+宽）×2=周长解：设此时长方形的宽为x米，则它的长为(x+1.4)米.根据题意，得(x+1.4+x)×2=10解得x=1.81.8+1.4=3.2此时长方形的长为3.2米，宽为1.8(2)若该长方形的长比宽多0.8米，此时长方形的长和宽各为多少米？它围成的长方形与(1)中所围成的长方形相比，面积有什么变化？xm(x+1.4)m解：设此时长方形的宽为x米，则它的长为（x+0.8）米.根据题意，得(x+0.8+x)×2=10解得x=2.12.1+0.8=2.9此时长方形的长为2.9米，宽为2.1米，面积为2.9×2.1=6.09(平方米)，(1)中长方形的面积为3.2×1.8=5.76(平方米).此时长方形的面积比(1)中长方形的面积增大6.09－5.76=0.33(平方米).(3)若该长方形的长与宽相等，即围成一个正方形，那么正方形的边长是多少？它围成的正方形的面积与(2)中相比，又有什么变化？xm(x+x)×2=10解得x=2.5正方形的面积为2.5×2.5=6.25(平方米)解：设正方形的边长为x米.根据题意，得比(2)中面积增大6.25-6.09=0.16（平方米）正方形的边长为2.5米同样长的铁丝可以围更大的地方例1用两根等长的铁丝分别绕成一个正方形和一个圆，已知正方形的边长比圆的半径长2(π－2)m，求这两根等长的铁丝的长度，并通过计算说明谁的面积大．典例精析[解析]比较两图形的面积大小，关键是通过题中的等量关系列方程求得圆的半径和正方形的边长，本题的等量关系为正方形的周长＝圆的周长．解：设圆的半径为rm，则正方形的边长为[r＋2(π－2)]m.根据题意，得答：铁丝的长为8πm，圆的面积较大．因为4π×4＞4π×π，所以16π＞4π2，所以圆的面积大．正方形的面积为[4＋2(π－2)]2＝4π2(m2)．所以圆的面积是π×42＝16π(m2)，所以铁丝的长为2πr＝8π(m)．2πr＝4(r＋2π－4)，解得r＝4.知识点二图形的等积変化某居民楼顶有一个底面直径和高均为4m的圆柱形储水箱．现该楼进行维修改造，为减少楼顶原有储水箱的占地面积，需要将它的底面直径由4m减少为3.2m．那么在容积不变的前提下，水箱的高度将由原先的4m变为多少米？合作探究1.如果设水箱的高变为xm，填写下表：旧水箱新水箱底面半径/m高/m体积/m3.列出方程并求解.2.根据表格中的分析，找出等量关系.21.64xπ×2×4π×1.6×x旧水箱的容积=新水箱的容积π×22×4π×1.62×x=解得x=5因此，水箱的高度变成了5m.例2一种牙膏出口处直径为5mm，小明每次刷牙都挤出1cm长的牙膏，这样一支牙膏可以用36次，该品牌牙膏推出新包装，只是将出口处直径改为6mm，小明还是按习惯每次挤出1cm的牙膏，这样，这一支牙膏能用多少次？解：设这一支牙膏能用x次，根据题意得π×522×10×36＝π×622×10·x.解这个方程，得x＝25.答：这一支牙膏能用25次．解：设这一支牙膏能用x次，根据题意得π×522×10×36＝π×622×10·x.解这个方程，得x＝25.答：这一支牙膏能用25次．你认为列一元一次方程解应用题的主要步骤有哪些？关键是什么？思考：1.审——通过审题找出等量关系.6.答——注意单位名称.5.检——检验求出的值是否为方程的解，并检验是否符合实际问题.4.解——求出方程的解(对间接设的未知数切忌继续求解).3.列——依据找到的等量关系，列出方程.2.设——设出合理的未知数(直接或间接)，注意单位名称.当堂练习1．三角形三边比是3:4:5，周长是72，那么，最长边是（）A．30B．24C．18D．12【答案】A【详解】设最长边是x，∵3+4+5=12，∴，∴x=30．故选：A．2．参加某次数学竞赛的女生和男生人数的比是1：3，这次竞赛的平均成绩是82分，其中男生的平均成绩是80分，女生的平均成绩是（）A．82分B．86分C．87分D．88分【答案】D【分析】根据题意，可找出数量间的相等关系:女生的平均成绩×1+男生的平均成绩×3=全班平均成绩×4，设女生的平均成绩是x，列方程解答即可．3．“和尚分馒头”问题是我国古代的数学名题之一，它出自明代数学家程大位写的《算法统宗》．书中的题目是这样的：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁？设有小和尚3x人，根据题意可列方程为（）A．3x+B．x+3(100-3x)=100C．x+D．x+3(100-x)=100【答案】B【分析】设有小和尚3x人，则大和尚的人数为（100-3x）人，然后根据三个小和尚一个馒头，一个大和尚三个馒头即可列出方程．【详解】解：设有小和尚3x人，则大和尚的人数为（100-3x）人，由题意得x+3(100-3x)=100，故选B．4．现有一个如图1所示的密封玻璃器皿，测得其底面直径为20cm，高为20cm，装有蓝色溶液若干.若如图2放置时，测得液面高为10cm；若如图3放置时，测得液面高为16cm，则该密封玻璃器皿总容积（结果保留m）为（）A．1250πcm3B．1300πcm3C．1350πcm3D．1400πcm3【答案】D【分析】根据圆柱体的体积公式和图②和图③中的溶液体积相等，可以列出相应的方程，从而可以解答本题．【详解】解：设该玻璃密封器皿总容量为Vcm³，π×10²×10=V-π×10²×（20-16），解得，V=1400π，故选D．5．根据市场调查，某种消毒液的大瓶装（500g）和小瓶装（250g）的销售瓶数的比为2：5．已知每天生产这种消毒液22.5吨，这些消毒液应该分装_______大瓶．【答案】20000【分析】设每份为x瓶，则大瓶销售了2x瓶，小瓶销售了5x瓶，根据大小消毒液的总重量为22.5吨=22500000克建立方程求出其解即可．【详解】解：设每份为x瓶，则大瓶销售了2x瓶，小瓶销售了5x瓶，根据题意得：2x×500+5x×250=22500000，解得x=10000，所以大瓶销售了：2×10000=20000瓶，故答案是：20000．6．已知一个两位数，其十位上的数字是个位上数字的3倍还少1，且它们的和是11，那么这个两位数是________．【答案】83【分析】设个位上数字是x，那么十位上数字3x-1，根据这两个数字之和等于11，可以列出方程x+3x-1=11，即可求出这个两位数．【详解】解：设个位上数字是x，十位上数字为3x-1，依题意得x+3x-1=11，整理得：4x=12，解得：x=3，3×3-1=8，所以这个两位数为83，故答案为：83．7．我国古代数学名著《张丘建算经》中记载：“今有清酒一斗直粟十斗，醐洒一斗直粟三斗，今持粟三斛，得酒五斗，问清跴酒各几何？”大意是：现有一斗清酒价值10斗谷子，一斗醐洒酒价值3斗谷子，现在拿30斗谷子，共换了5斗酒，问清洒，醐洒酒各几斗？如果设清酒x斗，那么可列方程为_________．【答案】10x+3(5-x)=30【分析】设清酒x斗，则醐洒酒为（5-x）斗，一斗清酒价值10斗谷子，x斗清酒价值10x斗谷子；一斗醐洒酒价值3斗谷子，（5-x）斗醐洒酒价值3（5-x）斗谷子．存在“换x斗清酒和（5-x）斗醐洒酒共用30斗谷子”的等量关系，根据等量关系可列方程．【详解】解：设清酒x斗，则醐洒酒为（5-x）斗．10x+3(5-x)=30故答案为：10x+3(5-x)=30．8．某学校组织秋游，原计划用45座的客车若干辆，则5人没有座位；如果用同样数量的50座客车，则多出一辆，且其余全部坐满．参加秋游的学生一共有_____名．【答案】500【分析】设原计划用车x辆，根据参加秋游的学生人数可列出方程，解方程即可求解．【详解】设原计划用车x辆，依题意有45x+5＝50（x1﹣），解得x＝11，50（x1﹣）＝50×（111﹣）＝500．故参加秋游的学生一共有500名．故答案为：500．9．冰墩墩是2022年北京冬季奥运会的吉祥物，将熊猫形象与富有超能量的冰晶外壳相结合，体现了追求卓越、引领时代，以及面向未来的无限可能．某学校购进了一批冰墩墩吉祥物分配给各班，若每班分4个，则剩余2个；若每班分5个，则还缺16个．求这个学校有几个班级？【答案】18【分析】设该学校有x个班级，则根据题意可列出关于x的一元一次方程，由此进行求解．【详解】解：设这个学校有x个班级，则4x+2=5x-16，解得x=18．答：这个学校有18个班级．10．某景区旅游团队的门票价格如下：购票人数不超过50人超过50人，但不超过100人超过100人门票价格120元/人100元/人80元/人（1）甲旅游团共有40人，则甲旅游团共付门票费元；（2）乙旅游团共付门票费9600元，则乙旅游团共有人；（3）丙，丁两个旅游团共有110人，其中丙旅游团人数不超过50人，两个旅游团先后共付门票费11800元，求丙、丁两个旅游团的人数．【详解】解：（1）甲旅游团共有40人，不超过50人，40×120＝4800（元），∴甲旅游团共付门票费4800元；（2）50人的门票费为：120×50=6000(元)，9600>6000，∴乙旅游团人数超过50人，当人数超过50人，但不超过100人，乙旅游团的人数＝9600÷100＝96（人）；当人数超过100人，乙旅游团的人数＝9600÷80＝120（人数）；综上所述，乙旅游团的人数为96或120；（3）丙，丁两个旅游团共有110人，其中丙旅游团人数不超过50人，∴丁旅游团的人数超过50人，但不超过100人，设丙旅游团人数为x人（0＜x≤50），则丁旅游团人数为（110x﹣）人，由题意可得：120x+100（110x﹣）＝11800，解得x＝40，∴110x﹣＝70（人），答：丙旅游团的人数为40人、丁旅游团的人数70人．课堂小结列⑤检{④解设审⑥答应用一元一次方程1、图形等长变化2、图形等积変化3、应用一元一次方程解决实际问题的步骤{