第十三章-轴对称复习-第1课时(知识要点)-八年级数学上册同步教材配套精品教学课件(人教版)

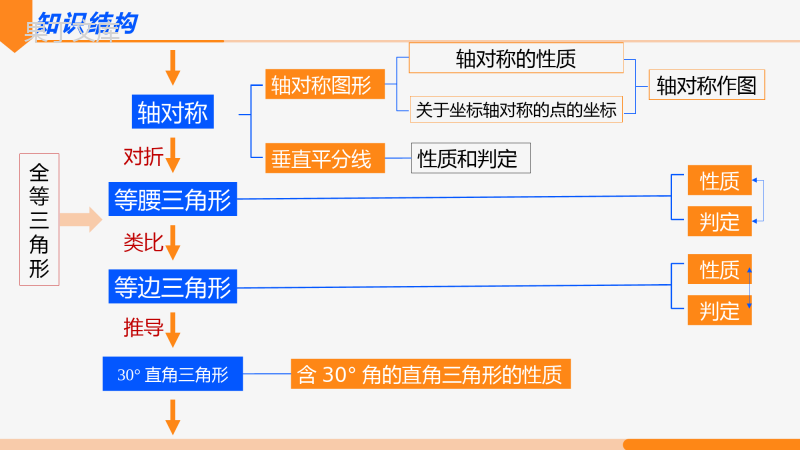
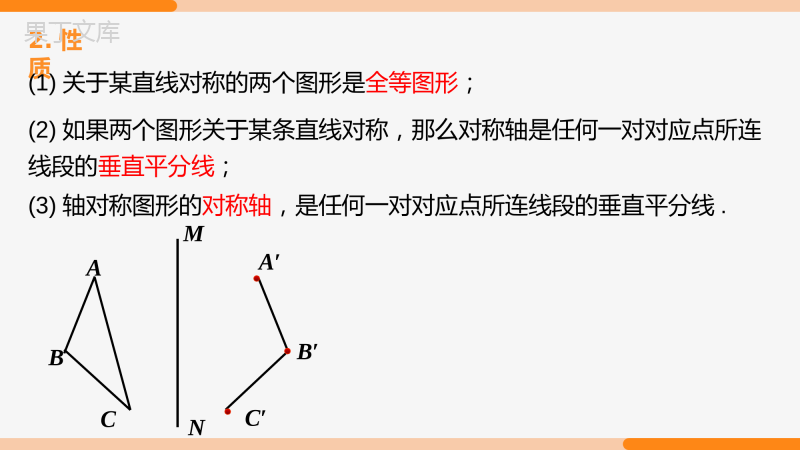
第十三章轴对称知识要点第十三章轴对称复习第十三章复习第1课时【学习目标】【学习目标】第十三章轴对称复习(第1课时)知识结构知识要点巩固训练知识结构轴对称等腰三角形等边三角形30°直角三角形对折类比推导轴对称图形垂直平分线轴对称的性质关于坐标轴对称的点的坐标轴对称作图性质和判定性质判定性质判定含30°角的直角三角形的性质全等三角形知识要点一、轴对称相关定义和性质(1)如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形这条直线就是它的对称轴；(2)如果一个平面图形沿一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称,这条直线就是它们的对称轴.1.定义(3)轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线.2.性质(1)关于某直线对称的两个图形是全等图形；(2)如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线；ABCA′B′C′NM二、垂直平分线的性质和判定(1)性质：线段垂直平分线上的点与这条线段两个端点的距离相等.(2)判定：与线段两个端点距离相等的点在这条线段的垂直平分线上．ABlP1P2P3BACMNM'N'P(1)点（x,y）关于x轴对称的点的坐标为(x,-y)三、平面直角坐标系中轴对称(2)点（x,y）关于y轴对称的点的坐标为(-x,y).xyABCDA′B′C′D′A′B′C′D′O四、等腰三角形的性质及判定等腰三角形边两腰相等三线合一三线角等边对等角证边相等证角相等对称轴性质判定边两边相等三线角等角对等边证边相等互逆五、等边三角形的性质及判定等边三角形边三条边相等每一边上的中线、高和这一边所对的角的平分线互相重合三线角三个角都相等，且都是60º性质判定边三条边相等边角角三个角相等互逆有一个角是60°的等腰三角形是等边三角形.等腰三角形类比六、含30°直角三角形在直角三角形中，30°角所对的直角边等于斜边的一半.在Rt△ABC中，∵∠C=90°，∠A=30°，∴BC=AB．12ABC12七、有关作图1.过已知直线外的一点作该直线的垂线2.作线段的垂直平分线3.最短路径：(1)将军饮马问题；(2)造桥选址问题ABCDABlB′CBAＭＮA'B'课堂练习1.在等腰三角形、圆、长方形、正方形、直角三角形中，一定是轴对称图形的有（）个A.1B.2C.3D.4D2.如图，∠3=30°，为了使白球反弹后能将黑球直接撞入袋中，那么击打白球时，必须保证∠1的度数为______.60°3.在直角坐标系中，点P(a,2)与点A(-3,m)关于y轴对称，则a,m的值分别为（）A.3，-2B.-3，-2C.3，2D.-3，2CABCMN4.如图：△ABC中，MN是AC的垂直平分线，若CM=3cm，△ABC的周长是22cm，则△ABN的周长是.16cm5.如图，△ABC中，∠A=36°，AB=AC,BD平分∠ABC交AC于点D,则图中的等腰三角形共有个.3BCDA6.如图，在△ABC中，∠ACB=90°，CD是高，∠A=30°，AB=4．则BD=.ABCD1证明：∵在△ABC中，∠ABC的平分线交AC于点D，∴∠ABD＝∠CBD.∵DE∥BC，∴∠EDB＝∠CBD.∴∠EBD＝∠EDB.∴BE＝DE.7．如图，在△ABC中，∠ABC的平分线交AC于点D，过点D作DE∥BC交AB于点E.(1)求证：BE＝DE；(2)若∠A＝80°，∠C＝40°，求∠BDE的度数．7．如图，在△ABC中，∠ABC的平分线交AC于点D，过点D作DE∥BC交AB于点E.(1)求证：BE＝DE；(2)若∠A＝80°，∠C＝40°，求∠BDE的度数．解：∵∠A＝80°，∠C＝40°，∴∠ABC＝60°.∵∠ABC的平分线交AC于点D，∴∠ABD＝∠CBD＝∠ABC＝30°.由(1)知∠BDE＝∠CBD，∴∠BDE＝30°.12128.如图，在△ABC中，AB=AC，∠ABC和∠ACB的平分线交于点O.过O作EFBC∥交AB于E，交AC于F.探究EF、BE、FC之间的关系.解：EF=BE+CF.理由如下：∵EFBC∥,∴∠EOB=∠CBO，∠FOC=∠BCO.∵BO、CO分别平分∠ABC、∠ACB，∴∠CBO＝∠ABO，∠BCO＝∠ACO，∴∠EOB＝∠ABO，∠FOC＝∠ACO，∴BE＝OE，CF=OF，∴EF=EO+FO＝BE+CF.ABCOEF8.如图，在△ABC中，AB=AC，∠ABC和∠ACB的平分线交于点O.过O作EFBC∥交AB于E，交AC于F.探究EF、BE、FC之间的关系.ABCOEF变式若AB≠AC，其他条件不变，图中还有等腰三角形吗？结论还成立吗？OABCEF