《汽车行驶的路程》人教版高中数学选修2-2PPT课件（第1.5.2课时）.pptx

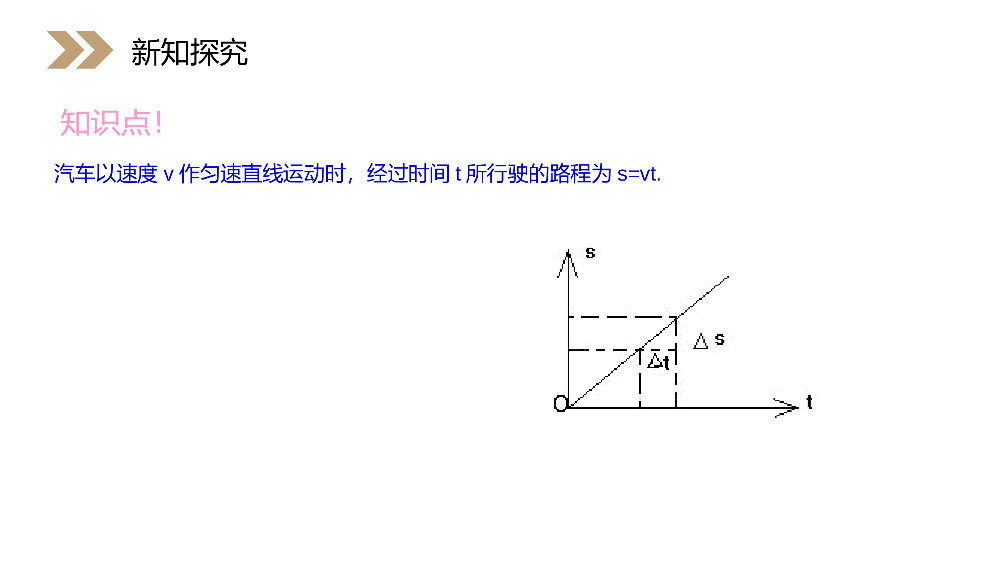
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-21.5.2汽车行驶的路程第1章导数及其应用人教版高中数学选修2-2中学学习过：三角形，圆形，矩形，平行四边形，梯形等规则图形面积的计算，而计算平面曲线围成的平面“曲边图形”的面积、变速直线运动物体位移、变力做功等问题.我们已学过了如何计算曲边图形面积.如何计算变速直线物体位移呢？课前导入利用导数我们解决了“已知物体运动路程与时间的关系，求物体运动速度”的问题.反之，如果已知物体的速度与时间的关系，如何求其在一定时间内经过的路程？提出问题课前导入汽车以速度v作匀速直线运动时，经过时间t所行驶的路程为s=vt.新知探究如果汽车做变速直线运动，在时刻t的速度为(t的单位：h，v的单位：km/h)，那么它在这段时间内行驶的路程s（单位：km）是多少？2v(t)=-t+20t1≤≤新知探究2v(t)=-t+20t1≤≤与求曲边梯形面积相似，我们采取“以不变代变”的方法，把求变速直线运动的路程问题，化归为求匀速直线运动的路程问题.新知探究将区间[0,1]等分成n个小区间，在每个小区间上.由于v(t)的变化很小.可以认为汽车近似做匀速直线运动，从而求得汽车在每个小区间上行驶路程的近似值，再求和得s的近似值，最后让n趋向于无穷大就得到s的精确值.1T2Txoi1tit1it1T2Txoi1tit1it在时间区间[0,1]上等间隔地插入n-1个分点，将它等分成n个小区间：112n-10,,,,,,1nnnn记第i个区间为，其长度为：i-1i,i=1,2,,nnnii-11Δt=-=nnn新知探究112n-10,,,,,,1nnnni-1i,i=1,2,,nnnii-11Δt=-=nnn把汽车在时间段上行驶的路程分别记作：112n-10,,,,,,1nnnnnii=1S=ΔS12nΔS,ΔS,,ΔS显然有新知探究112n-10,,,,,,1nnnnnii=1S=ΔS12nΔS,ΔS,,ΔS当n很大，即很小时，在区间上，函数的变化值很小，近似地等于一个常数.从物理意义上看，就是汽车在时间段上的速度变化很小，不妨认为它近似地以时刻处的速度作匀速行驶.i-1i,nnΔt2v(t)=-t+2i-1ni-1i,i=1,2,,nnn新知探究i-1i,nnΔt2v(t)=-t+2i-1ni-1i,i=1,2,,nnn2'ii2i-1i-11Δs=Δs=vΔt=-+2nnni-112=-+i=1,2,,nnnn在区间上，近似地认为即在局部小范围内认为“以匀速代变速”.i-1i,nn2i-1i-1v=-+2nn新知探究2'ii2i-1i-11Δs=Δs=vΔt=-+2nnni-112=-+i=1,2,,nnnni-1i,nn2i-1i-1v=-+2nn由近似代替求得：nn'nii=1i=12ni=12222233i-1ss=Δs=vΔtni-112=-+nnn111n-11=-0---+2nnnnn1=-1+2++n-1+2n1(n-1)n(2n-1)=-+2n6111=-1-1-+23n2n新知探究nn'nii=1i=12ni=12222233i-1ss=Δs=vΔtni-112=-+nnn111n-11=-0---+2nnnnn1=-1+2++n-1+2n1(n-1)n(2n-1)=-+2n6111=-1-1-+23n2nnnnni=1n1i-1s=lims=limvnn1115=lim-1-1-+2=3n2n3∞∞∞当n趋向于无穷大，即趋向于0时，趋向于s，从而有n111s=-1-1-+23n2nΔt新知探究nnnni=1n1i-1s=lims=limvnn1115=lim-1-1-+2=3n2n3∞∞∞n111s=-1-1-+23n2nΔt结合求曲线梯形面积的过程，你认为汽车行驶的路程s和由直线t=0，t=1,v=0和曲线所围成的曲边梯形的面积有什么关系？2v(t)=-t+2新知探究由于在数值上等于下图所有小矩形的面积之和.其极限就是由直线t=0，t=1,v=0和曲线所围成的曲边梯形的面积，从而汽车行驶的路程在数值上等于由直线t=0，t=1,v=0和曲线所围成的曲边梯形的面积.ns2v(t)=-t+22v(t)=-t+22v(t)=-t+2ns2v(t)=-t+22v(t)=-t+22v=-t+2xoya...新知探究2v=-t+2xoya一般地，如果物体做变速直线运动，速度函数为，那么我们也可以采用分割、近似代替、求和、取极限的方法，求出它在内的位移s.v=v(t)atb≤≤新知探究v=v(t)atb≤≤单位时间通过的路程小王驱车到80km外的一个小镇，共用了2个小时，(km/h)为汽车行驶的平均速度，然而车速器显示的速度（瞬时速度）却在不停地变化，因为汽车作的是变速运动，如何计算汽车行驶的瞬时速度呢?Δs80v===40Δt2例题讲解一般地：设S是某一物体从某一选定时刻到时刻t所走过的路程，则S是t的一个函数下面讨论物体在任一时刻t0的瞬时速度.S=S(t)Δs80v===40Δt2S=S(t)00[t,t+Δt]00ΔS=St+Δt-StsO0tstts000St+Δt-StΔSv==ΔtΔt瞬时速度内的平均速度为Δtt很小时，速度的变化不大，可以以匀速代替.例题讲解00[t,t+Δt]00ΔS=St+Δt-StsO0tstts000St+Δt-StΔSv==ΔtΔtΔtt0vtΔt0=limvΔt0ΔS=limΔt00Δt0St+Δt-St=limΔt越小，平均速度就越接近于时刻的瞬时速度令取极限，得到瞬时速度Δtv0tΔt0→0vt局部以匀速代替变速，以平均速度代替瞬时速度，然后通过取极限，从瞬时速度的近似值过渡到瞬时速度的精确值.例题讲解0vtΔt0=limvΔt0ΔS=limΔt00Δt0St+Δt-St=limΔtΔtv0tΔt0→0vt设汽缸内活塞一侧存有定量气体，气体做等温膨胀时推动活塞向右移动一段距离，若气体体积由变至，求气体压力所做的功（如下图）.OS1S2S1V2V课堂练习OS1S2S1V2V气体膨胀为等温过程，所以气体压强为(—气体体积，—常数），而活塞上的总压力为：CQCF=PQ==VS，CP=VVC课堂练习CQCF=PQ==VS，CP=VVC（—活塞的截面积，为活塞移动的距离）以与表示活塞的初始与终止位置，于是得功为QSVSQ1S2S22112121SSSSVVV2V11W=FdS=CdSS1=CdVVV=ClnV=Cln.V课堂练习QSVSQ1S2S22112121SSSSVVV2V11W=FdS=CdSS1=CdVVV=ClnV=Cln.V（1）分割1012n-1n2T=t