圆周角(第1课时)(课件)-2022-2023学年九年级数学上册同步精品课堂(苏科版)

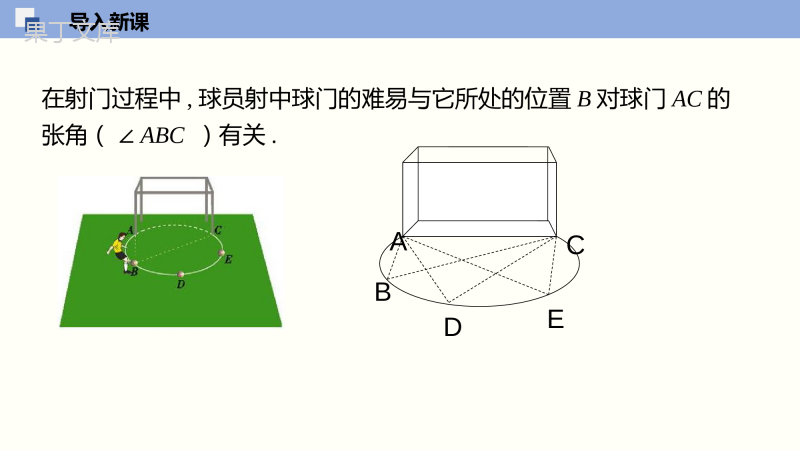
2.4圆周角第1课时圆周角与圆心角的关系数学（苏科版）九年级上册第2—章对称图形圆学习目标1．结合图形了解圆心角、圆周角的概念和区别；会叙述并且证明圆周角定理；2．利用圆心角与圆周角的关系解决与圆相关的几何问题；3．熟练掌握圆周角定理的推论，并学会其证明过程与应用；当堂检测知识回顾1.什么叫圆心角?.OAB顶点在圆心的角叫圆心角2.圆心角、弧、弦三个量之间关系的一个结论，这个结论是什么？在同圆（或等圆）中，如果圆心角、弧、弦有一组量相等，那么它们所对应的其余两个量都分别相等.导入新课在射门过程中,球员射中球门的难易与它所处的位置B对球门AC的张角（∠ABC）有关.ABCDE导入新课各抒己见：图中的∠ABC、∠ADC和∠AEC的顶点各在圆的什么位置？它们的两边和圆是什么关系？顶点在☉O上，角的两边分别与☉O相交.再思考一下：∠ABC、∠ADC和∠AEC的度数有什么关系呢？讲授新课知识点一圆周角的概念顶点在圆上，并且两边都与圆相交的角叫作圆周角.(如∠BAC)注：两个条件，缺一不可！我们把∠BAC叫作BC所对圆周角，BC叫作圆周角∠BAC所对的弧.⌒⌒讲授新课圆周角在我们生活中处处可见，比如，我们从团旗上的图案抽象出如图所示图形，图形中就有很多圆周角．E·AODBC典型例题例题1：判别下列各图形中的角是不是圆周角，并说明理由.不是不是是不是不是图1图2图3图4图5练一练·COAB·COB·COBAA·COAB·COB·COBAA判一判：下列各图中的∠BAC是否为圆周角,并简述理由.（2）（1）（3）（5）（6）顶点不在圆上顶点不在圆上边AC没有和圆相交√√√讲授新课知识点二圆周角定理及其推论图中的∠ABC、∠ADC和∠AEC都是AC所对的圆周角，我们知道在同圆或等圆中，相等的弧所对的圆心角相等，那么图中的三个圆周角有什么关系？⌒ABCE讲授新课为了弄清楚这三个角的关系，我们先来研究一条弧所对的圆周角和圆心角的关系.我们猜测也相等ABCDE讲授新课测量：如图，连接BO,CO,得圆心角∠BOC.测测看，∠BAC与∠BOC存在怎样的数量关系.12BACBOC测量与猜测猜测：圆周角的度数_______它所对弧上的圆心角度数的一半.等于12BACBOC讲授新课问题变动点A的位置，看看上述结论是否依然成立？AAA变动点A的位置，圆周角的度数没有变化，它的度数恰好为同弧所对的圆心角的度数的一半.讲授新课圆心O在∠BAC的内部圆心O在∠BAC的一边上圆心O在∠BAC的外部圆心O与圆周角的位置有以下三种情况，我们一一讨论.讲授新课与同桌或邻近桌的同学交流，猜测一条弧所对的圆周角与圆心角有什么关系．你能证明这个猜测吗？·AOCB情形一圆周角的一边通过圆心．如图圆O中，∠BAC的一边AB通过圆心．从而∠BOC=∠C+∠BAC=2∠BAC，由于OA=OC，因此∠C=∠BAC，12即∠BAC=∠BOC12∠BAC=∠BOC1212讲授新课·DAOCB情形二圆心在圆心角的内部如图，圆O在∠BAC的内部．作直径AD，根据情形一的结果得∠BAD=—————，∠DAC=—————．=——————从而∠BAC=∠BAD+∠DAC=——————12BOD12DOC12BODDOC12BOC12BOD12DOC12BODDOC12BOC讲授新课情形三圆心在圆周角的外部．12A·OBCD一条弧所对的圆周角等于它所对的圆心角的一半．综上所述，我们证明了下述定理：你能证明∠BAC=∠BOC吗？如图，圆心O在∠BAC的外部．证明:∵∠BAD=∠BOD∠CAD=∠COD∴∠BAD－CAD=(∠BOD-∠COD)∴∠BAC=∠BOC作直径AD121212121212121212讲授新课圆周角定理：圆周角的度数等于它所对弧上的圆心角度数的一半.圆周角定理及其推论A1A2A3推论1：同弧所对的圆周角相等.要点归纳典型例题BCO.70°A例题2、如图OA，OB，OC都是⊙O的半径，已知∠AOB=50°∠BOC=70°求∠ACB和∠BAC度数.∴∠ACB=∠AOB=25°同理∠BAC=∠BOC=35°解：∵圆心角∠AOB与圆周角∠ACB所对的弧为弧AB12121212练一练1.如图，AB是⊙O的直径，C是⊙O上的点，已知∠AOC=45°，则∠B=_______，∠A=_________；∠ACB=_______BACO.22.5°67.5°90°讲授新课2、如图，点A、B、C是圆O上的三点，且四边形ABCO是平行四边形，OFOC⊥交圆O于点F，则∠BAF等于（）A．12.5°B．15°C．20°D．22.5°练一练解析：连接OB，∵四边形ABCO是平行四边形，∴OC=AB，又OA=OB=OC，∴OA=OB=AB，∴△AOB为等边三角形，∵OFOC⊥，OCAB∥，∴OFAB⊥，∴∠BOF=AOF=30°∠，由圆周角定理得∠BAF=BOF=15°∠，故选：B．当堂检测答：（1）、（2）是圆周角，（3）、（4）不是圆周角，因（3）、（4）不满足圆周角定义，角顶点没在圆1.下图中各角是不是圆周角？请说明理由.（1）（2）（3）（4）当堂检测解：∵点A、B、C、D在⊙O上，∠BAC=35°，2、如图，点A、B、C、D在⊙O上，∠BAC=35°.求∠BDC、∠BOC的度数.∴∠BDC=∠BAC=35°.（同弧所对圆周角相等）∴∠BOC=2∠BAC=70°.（同弧所对的圆周角等于圆心角的一半）当堂检测3.如图，在圆O中，弦AB与CD相交于点M.若∠CAB=25°，∠ABD=95°，试求∠CDB和∠ACD的度数.圆周角∠ACD与圆周角∠ABD所对的弧均为，∵解：AD︵∠ACD=∠ABD=95°.∴同理∠CDB=∠CAB=25°.AD︵当堂检测4.如图，点A，B，C在⊙O上，AC∥OB.若∠OBA=25°，求∠BOC的度数.圆周角∠BAC与圆心角∠BOC所对的弧均为，∵BC︵∠BOC=2∠BAC=50°.∴解∵AC∥OB，∠OBA=25°，∠BAC=∠OBA=25°.∴BC︵当堂检测5.如图，在⊙O中，AB是直径，C，D是圆上两点，且AC=AD．求证：BC=BD.∵AC=AD，∴∠AOC=∠AOD.∴∠COB=∠DOB.∴BC=BD.证明连接CO、DO.当堂检测C6、如图，对于圆心O在圆周角∠APB外部的情形，证明∠APB=∠AOB.12证明：连接PO并延长交⊙O于点C.易知PO=BO=CO，∴∠OAP=∠OPA，∠OBP=∠OPB.由外角和定理易知∠COA=∠OAP+∠OPA=2∠OPA；∠COB=∠OBP+∠OPB=2∠OPB.而∠AOB=∠COB-∠COA=2∠OPB-2∠OPA=2∠APB.∴∠APB=∠AOB.121212当堂检测7、如图，∠ACB与∠ADB分别为⊙O上同一条弧AB所对的两个圆周角.（1）∠ACB与∠ADB之间具有怎样的大小关系？把你猜想和大家进行交流.（2）试证明你的猜想.（1）∠ACB=∠ADB（2）连接AO，BO，CO，DO.由同弧所对的圆周角等于所对的圆心角的一半可知：∠AOB=2∠ADB=2∠ACB.所以∠ACB=∠ADB.解：课堂小结一、这节课主要学习了两个知识点：1、圆周角定义.2、圆周角定理及其定理应用.“二、方法上主要学习了圆周角定理的证明渗透了特殊到”一般的思想方法和分类讨论的思想方法.三、圆周角及圆周角定理的应用极其广泛，也是中考的一个重要考点，望同学们灵活运用.课堂小结圆心角类比圆周角圆周角定义圆周角定理圆周角定理的推论1圆周角的度数等于它所对弧上的圆心角度数的一半.同弧或等弧所对的圆周角相等；1.顶点在圆上，2.两边都与圆相交的角谢谢~