同底数幂的乘法+课件-2022-2023学年人教版八年级数学上册-(2)

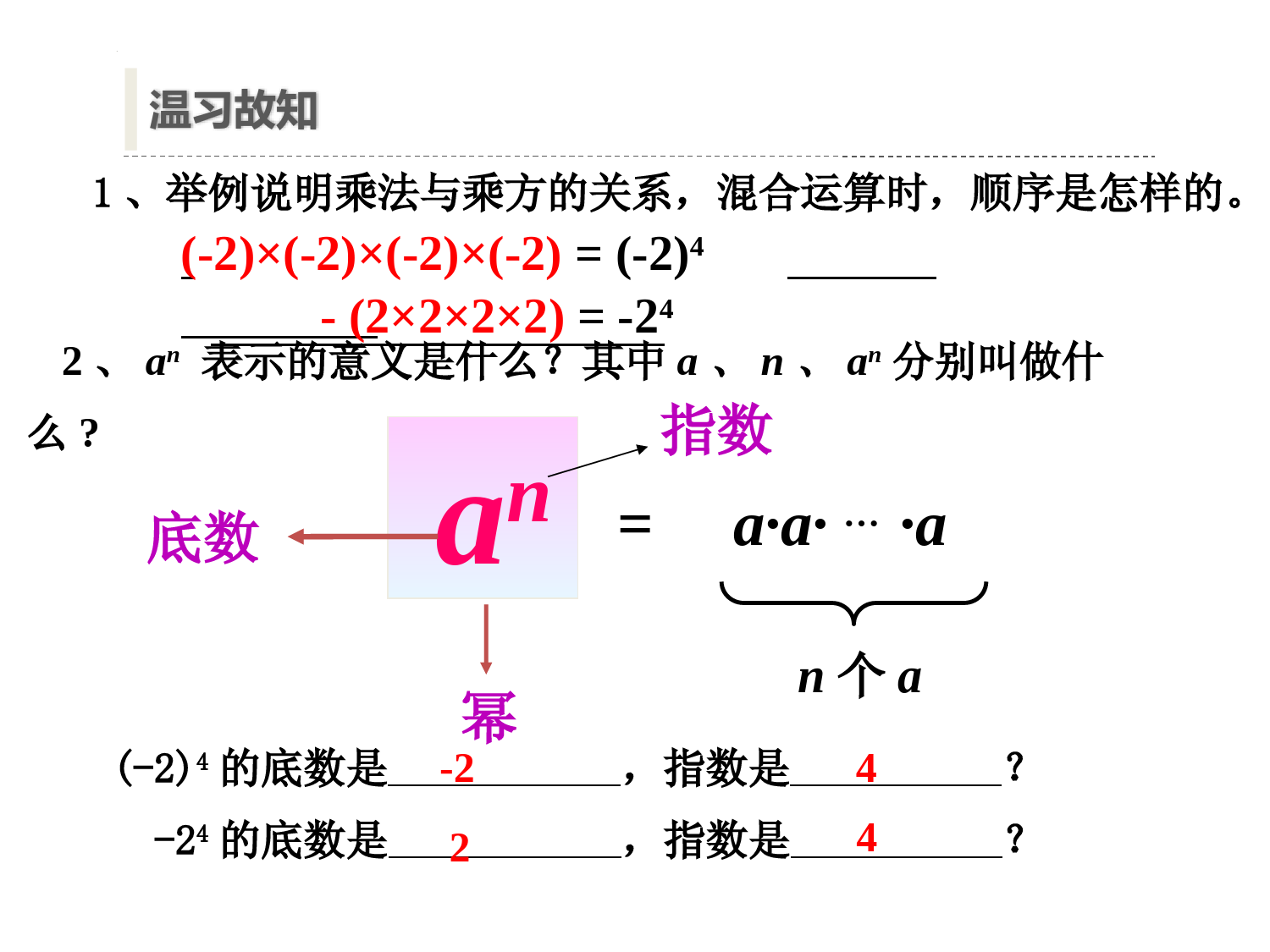
中物理人教版数学八年级上册第十四章整式的乘法与因式分解14.1整式的乘法14.1.1同底数幂的乘法前言学习目标重点运用同底数幂的乘法性质计算和应用。难点同底数幂的乘法性质的推导和灵活应用。1、感受生活中幂的运算的存在价值。2、经历自主探究同底数幂的乘法的运算性质的过程。能用代数式和文字表述性质，感受公式的抽象美、简洁美、对称美，并会用性质计算。3、逐步形成独立思考、主动探索的习惯，感悟科技的飞速发展和祖国的强大。4、通过由特殊到一般的猜想与说理、验证，培养学生归纳表达能力2021年10月16日，中国3名航天员翟志刚、王亚平、叶光富开启了6个月的空间生活。号称“快递小哥”的天舟三号，若要按时送达补给物资，需要精准的计算，如果使用的计算，每秒可达1016次运算,那么它工作103秒可进行多少次运算?情景导入1016×103=？=(10×10××10)‥‥‥19个=(10×10××10)×(10×10×10)‥‥‥=1019=a·a·…·an个a2、an表示的意义是什么？其中a、n、an分别叫做什么?an底数幂指数(-2)4的底数是，指数是？-24的底数是，指数是？(-2)×(-2)×(-2)×(-2)=(-2)4-(2×2×2×2)=-24温习故知1、举例说明乘法与乘方的关系，混合运算时，顺序是怎样的。-2244问题一：根据乘方的意义填空(结果写成幂的形式)。问题二：观察左右两边，底数、指数各有什么关系？问题三：得出你的猜想，并尝试证明你的猜想是否正确。(1).23×24=(2×2×2)×(2×2×2×2)=2(3+4)=2(7)(2).(—)3×(—)4=(××)×(×××)=(—)()=(—)()(3).0.53×0.54=(××)×(×××)=0.5()=0.5()(4).(-3)3×(-3)4=[××]×[×××]=(-3)()=(-3)()(5).a3·a4=(··)·(···)=a()=a()(7).(a+b)3×(a+b)4=[××]×[×××]=(a+b)()=(a+b)()探索新知232323(6).(mn)3×(mn)4=[××]×[×××]=(mn)()=(mn)()边思考边解答呦！23问题一：根据乘方的意义填空(结果写成幂的形式)。(1).23×24=2()(2).0.53×0.54=0.5()(3).(—)3×(—)4=(—)()(4).(-3)3×(-3)4=(-3)()(5).a3·a4=a()(6).(mn)3×(mn)4=(mn)()(7).(a+b)3×(a+b)4=(a+b)()3+4猜想:am·an=?(m、n都是正整数)3+43+43+43+4探索新知2323233+4问题二：观察左右两边，发现底数、指数各有什么规律？问题三：得出你的猜想，并尝试证明。3+4am·an==am+n=aa…a(m+n)个am个a（aa…a）n个a（aa…a）am·an=(m、n都是正整数)am+n（乘法结合律）（乘方的意义）归纳、证明证明:获得新知am·an=同底数幂相乘，底数，指数。不变相加同底数幂的乘法性质：am+n(m、n都是正整数)注意事项：1.条件：①底数相同，②乘法运算。2.结果：①底数不变，②将指数相加。如：43×45=43+5=481016×103=1019=(10×10×‥‥‥×10)×(10×10×10)=(10×10×‥‥‥×10)19个=1016+3简化运算，体验了公式的简洁美！应用新知解决问题同底数幂的乘法的性质：am·an=am+n(m、n都是正整数)想一想：当三个或三个以上同底数幂相乘时，是否也具有这一性质呢？怎样用公式表示？如am·an·ap？同底数幂的乘法的性质：am·an=am+n(m、n都是正整数)公式的推广例1计算，结果用幂的形式表示：(1)x2·x5；(2)a·a6；(3)(-2)×(-2)4×(-2)3；(4)xm·x3m+1a=a1同底数幂的乘法性质：am·an=am+n(m、n都是正整数)典型例题1、计算：(1)105×106=_____；(2)a7·a3=_______；(3)x5·x7=_______；(4)(-b)3·(-b)2=__________.2、判断下面的计算对不对？如果不对，应当怎样改正.(1)b3·b3=2b3(2)b3+b3=b6(3)a·a5·a3=a8(4)(-x)4·(-x)4=(-x)161011a10x12(-b)5=-b5××××b62b3=x8a9(-x)8同底数幂的乘法的性质：am·an=am+n(m、n都是正整数)基础训练（抢答）常见变形：(-a)2=a2,(-a)3=-a33、计算结果用幂的形式表示：(1)(-—)×(-—)2×(-—)3(2)y3×(-y)2(3)(a+b)4·(a+b)7(4)2m×2n×8同底数幂的乘法性质：am·an=am+n(m、n都是正整数)典型计算1313134、判断下面的说法是否正确，如果正确请说明理由，如果不正确请举出反例：两个幂相乘，如果底数不同就一定不能用性质计算。请计算：(x-y)2·(y-x)5.同底数幂的乘法的性质：am·an=am+n(m、n都是正整数)进阶练习方法总结:(1)当底数不同的幂相乘时，化为同底数的幂进行计算；(2)当底数互为相反数的幂相乘时，根据幂的符号规律,可把不同底数的幂化成同底数的幂相乘.，n为偶数，n为奇数(a-b)n=(b-a)n-(b-a)n常见变形：(-a)2=a2,(-a)3=-a3;5、2022年4月16日，搭载“太空三人组”的神州十三号载人飞船结束了6个月的“太空出差”。已知神舟飞船在轨道上运行的速度大约为7.8×103米/秒，接近第一宇宙速度，那么这半年（大约1.6×107秒）飞行了多少路程?实际应用解：(7.8×103)×（1.6×107）=(7.8×1.6)×(103×107)=12.48×1010答：太空三人组这半年共飞行了1.248×1011米。=1.248×1011（米）【想一想】am+n可以写成哪两个因式的积？公式的逆用am+n=am·an【填一填】若xm=3,xn=2,那么,(1)xm+n=×=×=；(2)x2m=×=×=_；(3)x2m+n=×=×=.xmxn632xmxm339x2mxn9218同底数幂的乘法的性质：am·an=am+n(m、n都是正整数)=()×()x10【试一试】6、(1)若xa=3,xb=4,求xa＋b的值．(2)已知23x＋2=32,求x的值；方法总结：(1)逆用同底数幂的乘法性质，将所求代数式转化为几个已知因式的乘积的形式，然后再求值.(2)将等式两边转化为底数相同的形式，然后根据指数相等列方程解答.拓展延伸同底数幂的乘法的性质：am·an=am+n(m、n都是正整数)；逆用：am+n=am·an(m、n都是正整通过对本节课的学习，你有哪些收获呢？同底数幂的乘法性质am·an=am+n(m,n都是正整数）注意同底数幂相乘，底数不变，指数相加am·an·ap=am+n+p(m,n,p都是正整数）直接应用公式常见变形：(-a)2n=a2n,(-a)2n+1=-a2n+1，底数相同时底数不相同时先变成同底数再应用公式课堂小结am·an=am+n(m,n都是正整数），n为偶数，n为奇数(a-b)n=(b-a)n-(b-a)n1.下列各式的结果等于26的是()A.2+25B.2·25C.23·25D.0.22·0.242.下列计算结果正确的是()A.a3·a3=a9B.m2·n2=mn4C.xm·x3=x3mD.y·yn=yn+13.计算：(1)xn+1·x2n=_______；(2)(a-b)2·(a-b)3=_______；(3)-a4·(-a)2=_____；(4)y4·y3·y2·y=_______.4.填空：(1)x·x2·x()=x7；(2)xm·()=x3m；(3)8×4=2x,则x=()BD45x2m-a6y10变式训练、自我检验同底数幂的乘法的性质：am·an=am+n(m、n都是正整数)；逆用：am+n=am·an(m、n都是正整数)x3n+1(a-b)5（2）=?（a）=?（a）=?（a）=?3344m4nm1、必做题目：课本第96页练习(2)(4)，习题14.1第1.(1)(2)题。2、开放性题目：请给你的同桌用2、3、a、b(a、b为正整数)编计算题。要求如下：(1)所编题目为同底数幂乘法计算题；(2)以上字母或者数字最多用两次。3、探究题目：用同底数幂相乘的运算法则计算并观察底数和指数的变化规律。（选做）课后作业与探究同底数幂的乘法的性质：am·an=am+n(m、n都是正整数)；逆用：am+n=am·an(m、n都是正整