北师大版--九年级上册--相似三角形复习课优质课件

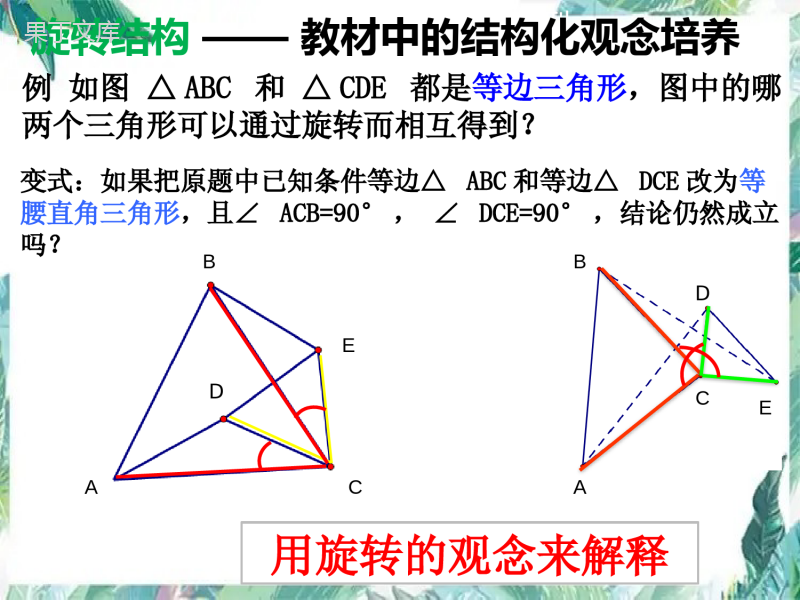
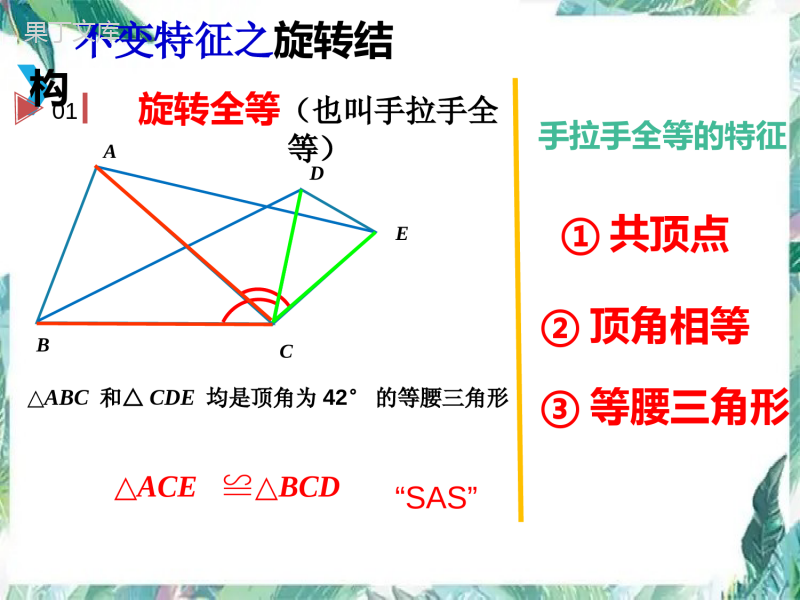
类比探究专项训练（一）——几何综合中的旋转结构①类比思路②寻找不变结构类比探究问题解题策略：常见结构如下：①中点结构“平行夹中点”“倍长中线”转移边、角②旋转结构找“等线段共端点”，借助全等、相似整合条件③平行结构作平行，造相似，转比例（A型，X型）④直角结构斜直角放正，找全等或相似学习目标1.认识并学会识别旋转结构。2.会运用类比、转化，找出几何图形中的旋转结构解决问题，形成规范的解题思路。几何综合中的手拉手模型旋转结构——教材中的结构化观念培养例如图△ABC和△CDE都是等边三角形，图中的哪两个三角形可以通过旋转而相互得到？BACEDDDACBDE变式：如果把原题中已知条件等边△ABC和等边△DCE改为等腰直角三角形，且∠ACB=90°，∠DCE=90°，结论仍然成立吗？用旋转的观念来解释ABCDE①共顶点②顶角相等③等腰三角形手拉手全等的特征△ACE≌△BCD01△ABC和△CDE均是顶角为42°的等腰三角形不变特征之旋转结构旋转全等（也叫手拉手全等）“SAS”①共顶点②顶角相等③相似三角形手拉手相似的特征△DAB∽△EAC02△ABC∽△ADE，∠DAE=∠BAC不变特征之旋转结构旋转放缩（也叫手拉手相似）“SAS”(中考真题.广西）已知：△ABC是等腰直角三角形，∠ACB=90°动点P在斜边AB所在的直线上，以PC为直角边作等腰直角三角形PCQ，其中∠PCQ=90°，探究并解决下列问题：（1）如图①，若点P在线段AB上，则线段PA、BQ之间的数量关系为；请直接写出PA²，PB²，PQ²三者之间的数量关系为；（2）如图②，若点P在AB的延长线上，在（1）中所猜想的结论仍然成立，请你利用图②给出证明过程.初步感知初步感知解：∵△ABC是等腰直角三角形，∴AC=CB,∠CAB=∠CBA=45°∵△PCQ是等腰直角三角形，∴PC=CQ∵∠ACB=∠PCQ=90°，∴∠ACB+∠PCB=∠PCQ+∠PCB即∠ACP=∠BCQ∴△ACP≌△BCQ∴PA=BQ，∠CBQ=∠CAB=45°∵∠ABQ=∠CBQ+∠CBA=90°∴∠PBQ==90°∴BQ²+PB²=PQ²∴PA²+PB²=PQ²典例（中考真题，22）如图①，在RtABC△中，∠B=90°,BC=2AB=8，点D,E分别是边BC，AC的中点，连接DE.将△EDC绕点C按顺时针方向旋转，记旋转角为α.（1）问题发现当α=0°时，AE=，BD=，=（2）拓展探究试判断：当0°≤α＜360°时，的大小有无变化？请仅就图2的情况给出证明.BDAEBDAE小试牛刀BDAEBDAE小试牛刀我对自己说---收获我对同学说---提醒我对老师说---困惑归纳提升△ACB∽△DCE△ACD∽△BCEADkBEACkBC“旋转结构”——相似EDCBAMαα“旋转结构”——全等△ACB,DCE△为等腰三角形，∠ACB=DCE∠△ACD≌BCE△ααCABEDM课堂小结ADkBEACkBC作业(中考真题·河南)(1)问题发现如图①，在△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝40°，连接AC，BD交于点M.填空：①AC/BD的值为________；②∠AMB的度数为________；(2)类比探究如图②，在△OAB和△OCD中，∠AOB＝∠COD＝90°，∠OAB＝∠OCD＝30°，连接AC交BD的延长线于点M.①AC/BD的值为____；②∠AMB的度数为_____；