北师大版--九年级上册--相似三角形复习课优质课件

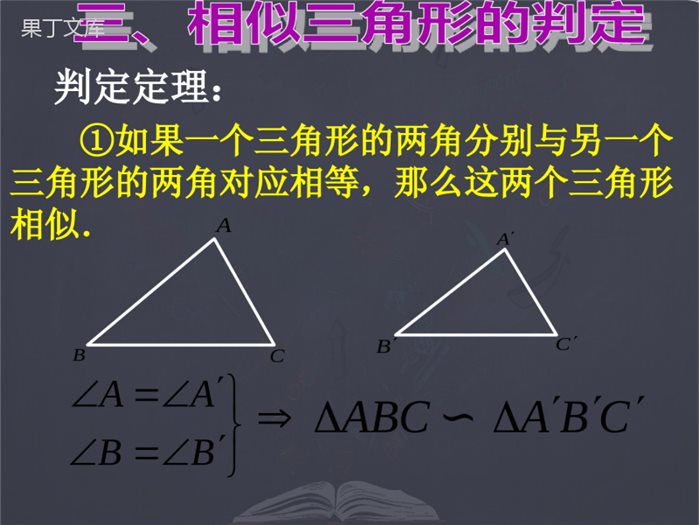
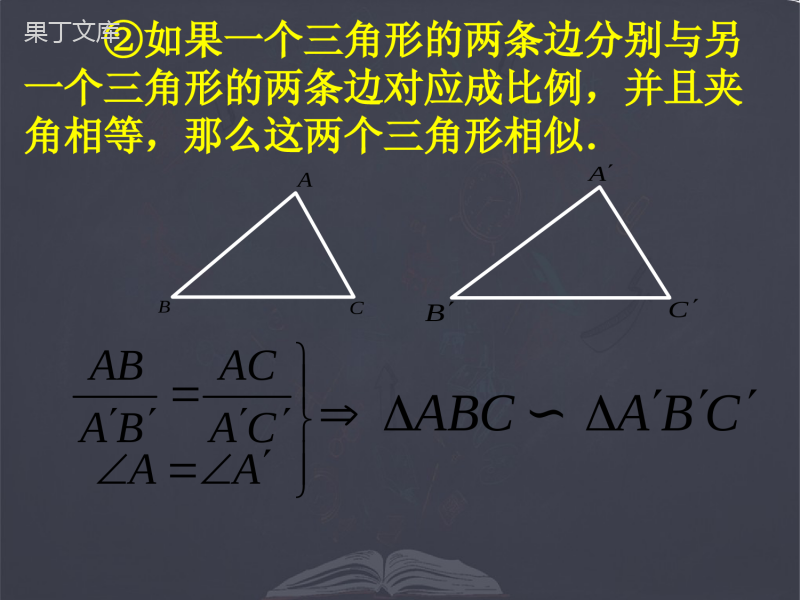
1.相似三角形的定义：对应角相等、对应边成比例的三角形叫做相似三角形。2.相似比：相似三角形的对应边的比，叫做相似三角形的相似比。★△ABC∽△A/B/C/,如果BC=3,B/C/=1.5,那么△A/B/C/与△ABC的相似比为_________.1:2（1）相似三角形的对应边成比例，对应角相等；（2）它们的对应高、对应中线、对应角平分线的比等于相似比；（3）它们的周长的比等于相似比；面积的比等于相似比的平方。判定定理：ABCCAB①如果一个三角形的两角分别与另一个三角形的两角对应相等，那么这两个三角形相似．CBAABC∽BBAA②如果一个三角形的两条边分别与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似．ABCCABCBAABC∽AACAACBAAB③如果一个三角形的三条边分别与另一个三角形的三条边对应成比例，那么这两个三角形相似．ABCCABCBAABC∽CBBCCAACBAAB巩固练习判断下列命题①所有的等腰三角形都相似．②所有的直角三角形都相似．③所有的等边三角形都相似．④所有的等腰直角三角形都相似．(×)(√)(√)(×)小结：相似的形式一）如图1，当时，△ABCADE∽△ABCDE图1）如图2，当时，△ABCAED∽△。ABCDE图2）如图3，当时，△ABCACD∽△。ABCD图3DEBC∥∠AED=B∠∠ACD=B∠一、基本图形(母子相似或A型)ABCDEABCDEABCD1）如图1，当ABED∥时，则△∽△，当.ABCDE图1A′B′C′D′E′图2ABCDEC∠B′=E∠′或△A′B′C′∽△D′E′C′小结：相似的形式二∠A′=D∠′或////////CECBCDCA二、（兄弟相似或X型）ABCDEA’B’C’D’E’ABCDBCAD∵∠BAC=90°,∴△ABCDBADAC∽△∽△小结：相似的形式三特殊图形（双垂直型）1、如图1,已知:DEBC,EFAB,∥∥则图中共有_____对三角形相似.3ABCDEF如图(1)2:已知,如图,梯形ABCD中,ADBC,∥A=90∠0,对角线BDCD⊥求证:(1)ABDDCB;△∽△(2)BD2=AD·BCABCD证明:(1)ADBC,∵∥∴∠ADB=DBC∠∵∠A=BDC=90°,∠∴△ABDDCB∽△(2)ABDDCB∵△∽△∴AD=BDBDBC即:BD2=AD·BC3如图，正方形ABCD的边长为8，E是AB的中点，点M，N分别在BC，CD上，且CM=2，则当CN=_________时，△CMN与△ADE形状相同。EABCDMN1或4ABEDCMN解：当CN=1时，AD：CM=AE：CN=2：1△CMN∽ADE△解：当CN=4时，AD：CN=AE：CM=2：1△CMN∽ADE△4、如图，△ABC是一块锐角三角形余料，边长BC=120毫米，高AD=80毫米，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是多少？NMQPEDCBA解：设正方形PQMN的边长为x毫米.∵PNBC∥，∴△APNABC∽△x=48答：正方形零件的边长是45毫米。BCPNADAE1208080xx5、在方格纸中，每个小格的顶点称为格点，以格点的连线为边的三角形称为格点三角形，如图所示的5×5的方格纸中，如果想作格点ΔABC与ΔOAB相似(相似比不能为1)，则C点坐标为____________．OxAByOxABy125C1(5，2)55252C2(4，4)补充练习：•1、已知：平行四边形ABCD，E是BA延长线上一点，CE与AD、BD交于G、F，求证：ABCDFGEEFGFCF22、矩形ABCD中，AB＝4，BC＝6，M是BC的中点，DE⊥AM，E是垂足。求DE的长。EMDCBA•这节课我们复习了哪些知识？•这节课你的收获是什么？•完成总复习中对应的内容