北师大版--九年级上册--一元二次方程复习-优质课件

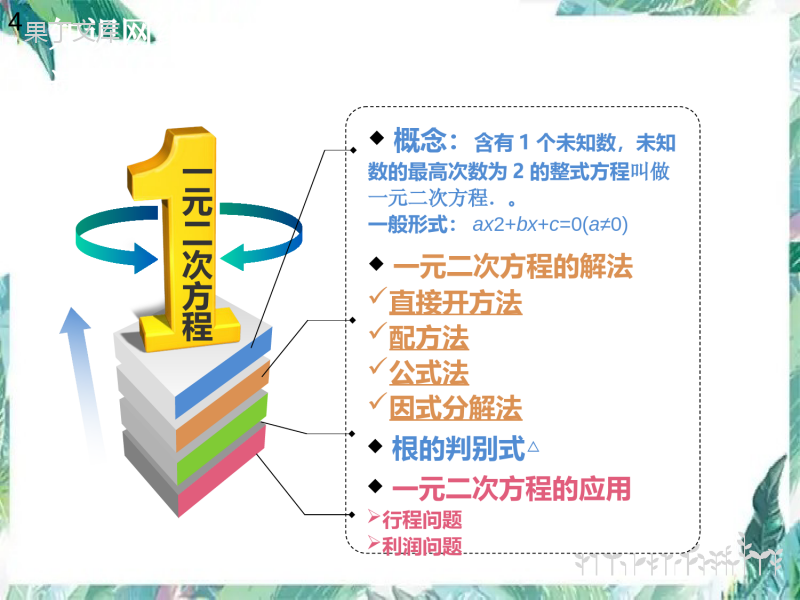
一元二次方程复习（一）好好学习！天天向上！复习流程考点导学——综合讲解··各个击破考场误区——及时点醒··游刃有余中考乐园——勤奋求索··走向成功5234你准备好了吗？1考情分析——及时了解·心中有数6小结反思——及时反思··成就梦想3知识网络——提纲挈领··一览无遗好好学习！天天向上！知识网络——提纲挈领·一览无遗◆概念：含有1个未知数，未知数的最高次数为2的整式方程叫做一元二次方程．。一般形式：ax2+bx+c=0(a≠0)◆一元二次方程的解法直接开方法配方法公式法因式分解法◆一元二次方程的应用行程问题利润问题◆根的判别式△一元二次方程4好好学习！天天向上！考情分析—及时了解·心中有数考试要求命题规律①理解一元二次方程的概念及一般形式；②理解配方法，会用直接开方法、配方法、公式法、因式分解法解含有数字系数的一元二次方程；③会用一元二次方程根的判别式判别方程是否有实根常考点是选择合适的方法解一元二次方程，用方程根的判别式判断方程根的情况或者根据根的情况求字母系数的取值范围5好好学习！天天向上！考点导学—综合讲解··各个击破考点一一元二次方程的定义及一般形式例1、下列方程是关于x的一元二次方程的是（）A、x2+3=1/xB、（2x+3）（2x-3）=4x2-2x+3C、x2+2x+y=0D、（a2+1）x2+bx+c=0小结：一元二次方程的定义：只含有__1___个未知数，并且未知数的最高次数是__2____的整式方程叫做一元二次方程．D6好好学习！天天向上！考点一一元二次方程的定义及一般形式考点导学—综合讲解··各个击破例2、方程（m+2）x︱m︳+3mx+1=0是关于x的一元二次方程，则m的值为分析：∵︳m︳=2m=±2m=2∴∴m+2≠0m≠-22小结：一元二次方程的一般形式：ax2+bx+c=0(a≠0)7好好学习！天天向上！考点一一元二次方程的定义及一般形式考点导学—综合讲解··各个击破8课堂即时训练1、下列是关于x的一元二次方程的有①②x2+1=0③（2x-1)2=（x-1)(4x-3)④k2x2+5x+6=0⑤⑥3x2+2-2x=0021xx243202x3x122、关于x的方程（m-3）x︱m︳-1-2x+4=0是一元二次方程，则m的值为②⑤⑥-3好好学习！天天向上！考点导学—综合讲解··各个击破例3、你是个会“精挑细选”的学生吗？请选择合适的求解方法.2712352x0322tt054342xx0233232xx018962yy96412xx直接开方法配方法公式法因式分解法公式法因式分解法因式分解法当方程一边能够分解为两个因式乘积的形式，一边等于0，可以优先用因式分解法.其中分解因式有提取公因式，运用平方差、完全平方公式，十字相乘等方法.直接开方法当方程可化成形如x2=a（a≥0）；（mx+n）2=b（m、n为常数，b≥0）形式，用直接开方法最简单.配方法可用于任何一个一元二次方程，但是除了形如x2+2kx+c=0（即二次项系数为1，一次项系数为偶数，常数项不为0）用配方法外，一般不用.配方法公式法是可用于任何一个一元二次方程，但不一定是最简单的.因此解方程时优先考虑能否应用“直接开方法”“因式分解法”等简单方法，若不行，再考虑.公式法直接开方法配方法因式分解法公式法优先选取顺序依次为：考点二一元二次方程的解法9好好学习！天天向上！考点三一元二次方程根的判别式考点导学—综合讲解··各个击破例4、方程x2+3x+4=0的解的情况（）A、2个相等的解B、2个不相等的解C、无解D、3个不相等的解C分析：∵△=—4×1×4=9—16=-7＜0，∴此方程无实数根小结：一元二次方程ax2+bx+c=0(a≠0)的根的判别式为△=b2-4ac当b2-4ac0时方程有两个不相等的实根．当b2-4ac0时方程有两个相等的实数根．当b2-4ac0时方程没有实数根．当b2-4ac0时方程有实数根．＞＝＜≥10好好学习！天天向上！考点导学—综合讲解··各个击破考点三一元二次方程根的判别式课堂即时训练1、请用最快的速度把下列方程的序号填入相应的横线内（1）-2x2-x+3=0（2）x2+9=0（3）6x2-5x=4（4）2x（x+2）+35=0（5）x2+9=3x（6）x2+3x=0有两个不相等的实数根的方程的序号是有两个相等的实数根的方程的序号是没有实数根的方程的序号是（1）（2）（3）（6）（4）（5）11好好学习！天天向上！考点导学—综合讲解··各个击破考点三一元二次方程根的判别式课堂即时训练2、已知关于x的一元二次方程x2－(k＋3)x＋3k＝0.(1)求证：不论k取任何实数，该方程总有实数根；(2)若等腰△ABC的一边长为2，另两边长恰好是这个方程的两个根，求△ABC的周长．12好好学习！天天向上！考点导学—综合讲解··各个击破考点三一元二次方程根的判别式课堂即时训练(1)证明：Δ＝(k＋3)2－4×3k＝(k－3)2≥0，故不论k取何实数，该方程总有实数根．(2)解：当△ABC的底边长为2时，方程有两个相等的实数根，则(k－3)2＝0，解得k＝3，方程为x2－6x＋9＝0，解得x1＝x2＝3，故△ABC的周长为：2＋3＋3＝8；当△ABC的一腰长为2时，方程有一根为2，解得k＝2，方程为x2－5x＋6＝0，解得x1＝2，x2＝3，故△ABC的周长为：2＋2＋3＝7.13好好学习！天天向上！考场误区——及时点醒··游刃有余你开动脑筋了吗？误区：判断未知系数的取值范围时考虑不全【例】关于x的一元二次方程(a－1)x2＋x＋a2－1＝0的一个根是0，则a的值为()A.1B.-1C.1或-1D.B分析：将x＝0代入原方程得到关于a的方程，求解a即可．依题意得(a－1)×02＋0＋a2－1＝0，解得a＝±1.(∵a－1)≠0，∴a＝－1.故选B.易错警示切记不要忽略一元二次方程二次项系数不为零这一隐含条件．14好好学习！天天向上！考场误区——及时点醒··游刃有余你准备好了吗？1、关于x的方程kx2－4x－2/3＝0有实数根，则k的取值范围是____________课堂即时训练k≥-615分析：①当方程是一元二次方程时，△≥0且k≠0即（-4）2+4×k×2/3≥0且k≠0∴k≥-6且k≠0②当方程是一元一次方程时，k=0综上所得k≥-6好好学习！天天向上！2、已知m为非负整数，且关于x的一元二次方程（m-2）x2—（2m-3）x+m+2=0有两个实数根，求m的值。课堂即时训练解：∵关于x的一元二次方程（m-2）x2—（2m-3）x+m+2=0有两个实数根∴△=b2-4ac≥0即〔-（2m-3）〕2—4（m-2)（m+2）≥04m2-12m+9-4m2+16≥0解得m≤25/12∵m为非负整数∴m=0,1,2又∵m-2≠0m≠2∴∴m的值为0或116考场误区——及时点醒··游刃有余你准备好了吗？好好学习！天天向上！2、已知m为非负整数，且关于x的一元二次方程（m-2）x2—（2m-3）x+m+2=0有两个实数根，求m的值。课堂即时训练变式一：已知m为非负整数，且关于x的方程（m-2）x2—（2m-3）x+m+2=0有两个实数根，求m的值。17考场误区——及时点醒··游刃有余你准备好了吗？变式二：已知m为非负整数，且关于x的方程（m-2）x2—（2m-3）x+m+2=0有实数根，求m的值。好好学习！天天向上！中考乐园——勤奋求索·成就梦想你充满信心了吗？请好好欣赏广东省的中考题.1、（中考真题）关于x的一元二次方程x23x+m=0﹣有两个不相等的实数根，则实数m的取值范围为（）A．m＞9/4B．m＜9/4C．m=9/4D．m＜-9/4B2、(2015广东省，8，3分)若关于x的方程有两个不相等的实数根，则实数a的取值范围是（）A、a≥2B、a≤2C、a＞2D、a＜2C18好好学习！天天向上！中考乐园——勤奋求索·成就梦想你充满信心了吗？请好好欣赏广东省的中考题.3、(中考真题)解方程：x2－3x+2＝019好好学习！天天向上！小结反思——及时反思··成就梦想谈谈你对这节课的认识，你还有什么疑问，我们共同解决知识方面解题方面方法方面其他方面20谢谢！