湘教版数学八年级上册-《全等三角形(5)》习题课件2

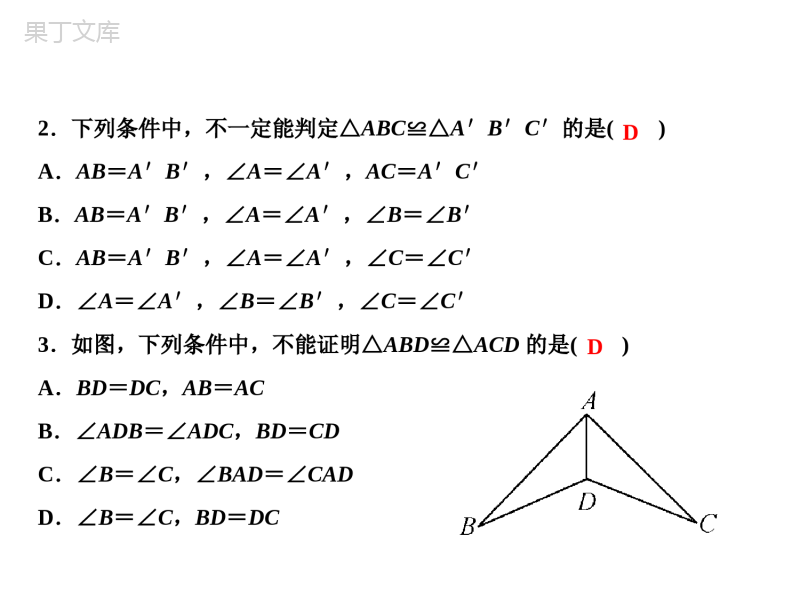
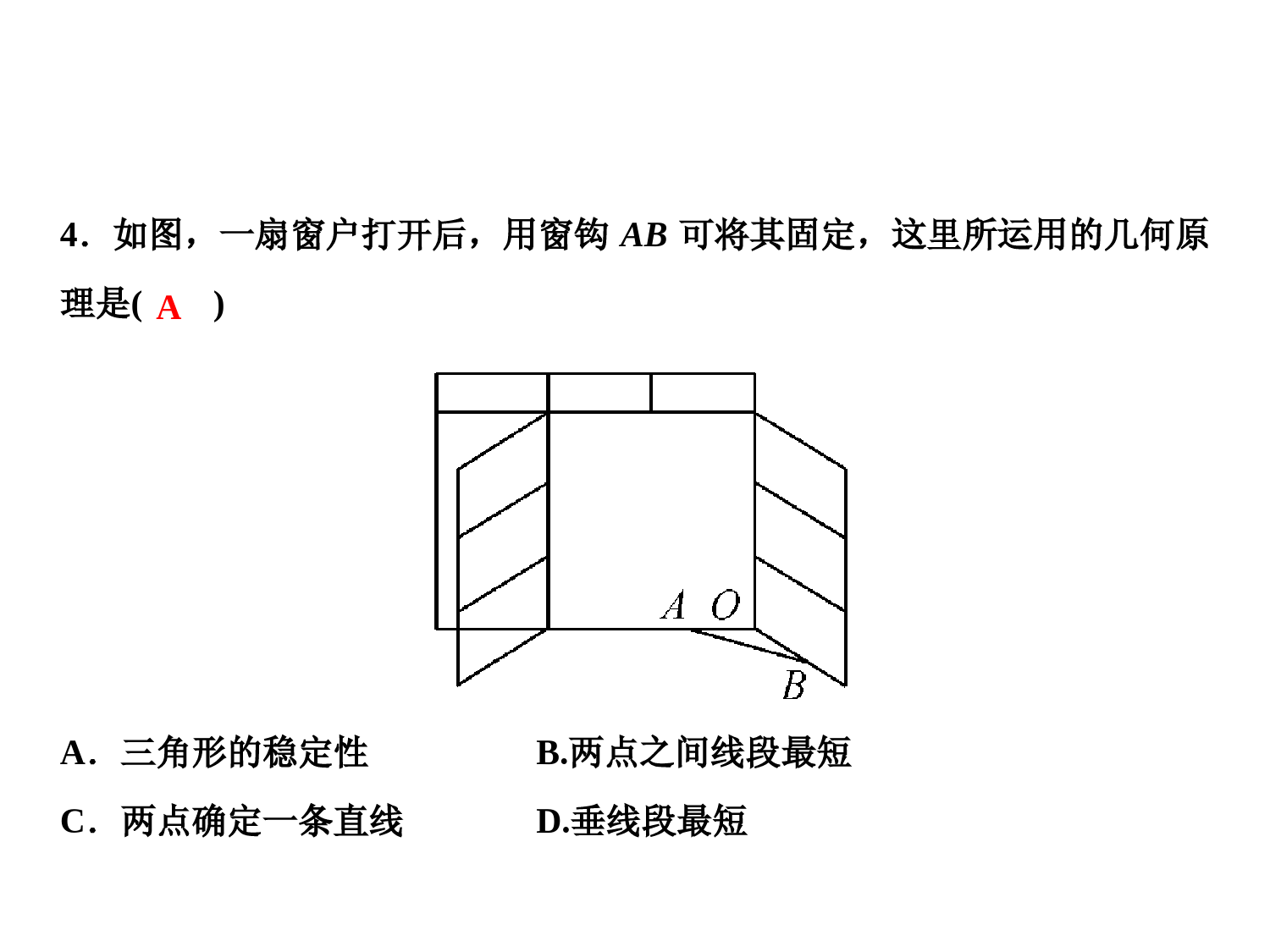
边边边定理：的两个三角形全等，可简写成“”或“”．自我诊断.如图，AB＝AD，要根据“SSS”判定△ABC≌△ADC，还需添加的条件是.三边分别相等边边边SSSBC＝DC三角形的三边长度固定，则三角形的形状和大小也固定了，三角形的这个性质叫作.易错点.误认为两边及一边的对角对应相等，以及三个角分别相等的两个三角形也全等．三角形的稳定性1．如图，已知AB＝CD，AD＝BC，则下列结论：①△ABD≌△CDB；②△ABC≌△CDA；③∠ABD＝∠CDB；④∠BAD＝∠DCB.其中正确的个数是()A．1个B.2个C．3个D.4个D2．下列条件中，不一定能判定△ABC≌△A′B′C′的是()A．AB＝A′B′，∠A＝∠A′，AC＝A′C′B．AB＝A′B′，∠A＝∠A′，∠B＝∠B′C．AB＝A′B′，∠A＝∠A′，∠C＝∠C′D．∠A＝∠A′，∠B＝∠B′，∠C＝∠C′3．如图，下列条件中，不能证明△ABD≌△ACD的是()A．BD＝DC，AB＝ACB．∠ADB＝∠ADC，BD＝CDC．∠B＝∠C，∠BAD＝∠CADD．∠B＝∠C，BD＝DCDD4．如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是()A．三角形的稳定性B.两点之间线段最短C．两点确定一条直线D.垂线段最短A5．如图，四边形ABCD中，AB＝BC，AD＝CD.求证：∠A＝∠C.证明：连接BD，在△ABD和△CBD中，AB＝CBBD＝BDAD＝CD，∴△ABD≌△CBD(SSS)．∴∠A＝∠C.6．如图，在△ABC中，AB＝AC，点D是BC的中点，E在AD上．求证：(1)△ABD≌△ACD；(2)BE＝CE.证明：(1)∵D为BC中点，∴BD＝CD，∵AB＝AC，AD＝AD，∴△ABD≌△ACD(SSS)；(2)∵△ABD≌△ACD，∴∠BAE＝∠CAE，∵AB＝AC，AE＝AE，∴△BAE≌△CAE(SAS)，∴BE＝CE.7．如图，△ABC中，AB＝AC，EB＝EC，则由“SSS”可以判定()A．△ABD≌△ACDB.△ABE≌△ACEC．△BDE≌△CDED.以上答案都不对B8．如图，D是BC的中点，要直接用“SSS”判定△ABD≌△ACD，需要添加的一个条件是()A．∠ADB＝∠ADCB.∠BAD＝∠CADC．AB＝ACD.AD＝CDC9．如图，线段AD与BC交于点O，且AC＝BD，AD＝BC，则下面结论中不正确的是()A．△ABC≌△BADB.∠CAB＝∠DBAC．OB＝OCD.∠C＝∠DC10．已知一等腰三角形的腰长为5，底边长为4，底角为β，满足下列条件的三角形不一定与已知三角形全等的是()A．两条边长分别为4、5，它们的夹角为βB．两个角是β，它们的夹边为4C．三条边长分别是4、5、5D．两条边长是5，一个角是βD11．如图，已知AC＝BD，要使△ABC≌△DCB，则只需添加一个适当的条件是(填一个即可)．∠ACB＝∠DBC12．如图，AB＝BC，AD＝CD，∠ABC＝80°，∠ADC＝50°，则∠A＝度．11513．已知：如图，A、C、F、D在同一直线上，AF＝DC，AB＝DE，BC＝EF，求证：△ABC≌△DEF.证明：∵AF＝DC，∴AF－CF＝DC－CF，即AC＝DF.在△ABC和△DEF中，AC＝DFAB＝DEBC＝EF，∴△ABC≌△DEF(SSS)．14．如图，AD＝CB，AB＝CD，BE⊥AC，垂足为E，DF⊥AC，垂足为F.求证：(1)△ABC≌△CDA；(2)BE＝DF.证明：(1)∵AB＝CD，AD＝CB，AC＝CA，∴△ABC≌△CDA(SSS)；(2)∵△ABC≌△CDA，∴∠BAC＝∠DCF，∵BE⊥AC，DF⊥AC，∴∠AEB＝∠CFD，又∵AB＝CD，∴△ABE≌△CDF(AAS)，∴BE＝DF.15.已知，如图，AB＝DC，AC＝BD，AC与BD交于O点．求证：△AOB≌△DOC.证明：在△ABC和△DCB中，AB＝DCAC＝BDBC＝CB，∴△ABC≌△DCB(SSS)，∴∠1＝∠2.在△AOB和△DOC中，∠3＝∠4∠1＝∠2AB＝DC，∴△AOB≌△DOC(AAS)．