2021年中考数学复习：瓜豆原理专题-第1题

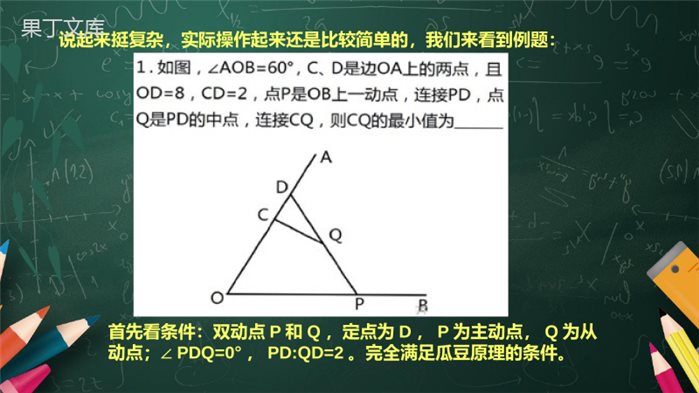
最值问题-瓜豆原理中考专项练习瓜豆原理初中数学中，双动点的最值问题，很大一部分是使用瓜豆原理解决的，那什么情况下使用瓜豆原理呢？当存在两个动点，一个定点，且符合以下条件时，可以使用瓜豆原理：1、两个动点A和B，其中一个是主动点，另一个是从动点，也就是A和B的运动是关联的，而能是各自随意运动；2、动点A和B到定点C的夹角始终不变；3、线段AC和BC的比值始终不变；当满足以上条件时，我们可以使用瓜豆原理。瓜豆原理-直线当我们确定可以使用瓜豆原理时，我们可以使用瓜豆原理的以下结论：（设∠ACB=α，AC:BC=λ）1、从动点的轨迹与主动点的轨迹相同：主动点轨迹为圆，则从动点轨迹也是圆；当主动点轨迹为直线，则从动点轨迹也为直线；2、当轨迹为直线时：a,从动点的轨迹长度与主动点的轨迹长度之比为λ；b,从动点与主动点轨迹的夹角=α；瓜豆原理-圆当我们确定可以使用瓜豆原理时，我们可以使用瓜豆原理的以下结论：（设∠ACB=α，AC:BC=λ）1、从动点的轨迹与主动点的轨迹相同：主动点轨迹为圆，则从动点轨迹也是圆；当主动点轨迹为直线，则从动点轨迹也为直线；2、当轨迹为圆时：a,从动点的轨迹圆与主动点的轨迹圆半径之比为λ；b,从动点圆心O,定点C,主动点O’连线的夹角∠OCO’=α；说起来挺复杂，实际操作起来还是比较简单的，我们来看到例题：首先看条件：双动点P和Q，定点为D，P为主动点，Q为从动点；∠PDQ=0°，PD:QD=2。完全满足瓜豆原理的条件。结论：1、P轨迹为射线，则Q轨迹同为射线；2、轨迹长度之比为2；3、轨迹的夹角=PDQ=0°∠，即两直线平行；当P与O重合是，Q点位于OD的中点F；过F做FE平行OB,做CMFE⊥；CM即为CQ的最小值；在△CMF中，CF=1/2OD-CD=4-2=2，∠CFM=60°，∴CM=感谢您的观看下节课再见