《函数的最大（小）值与导数》人教版高中数学选修2-2PPT课件（第1.3.3课时）.pptx

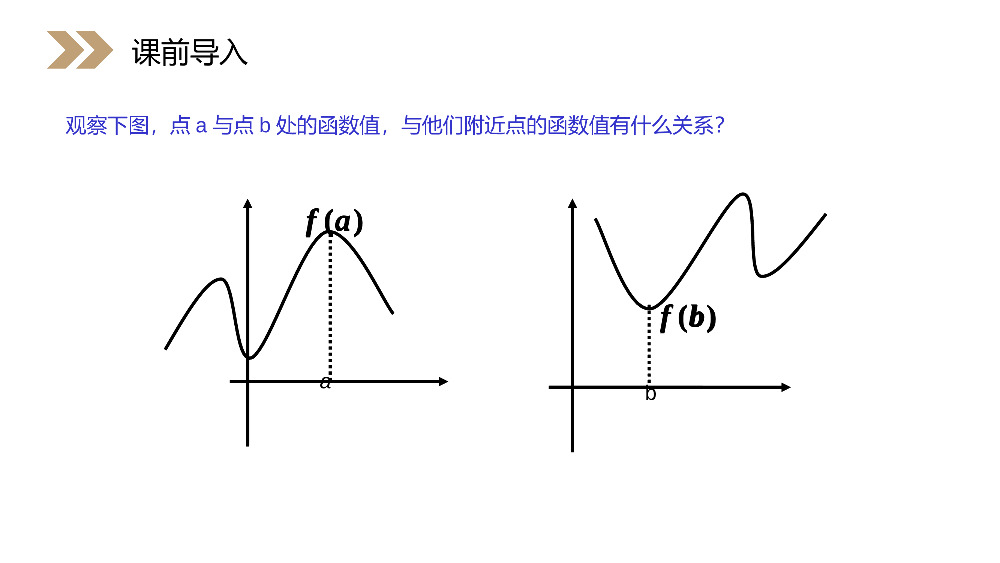
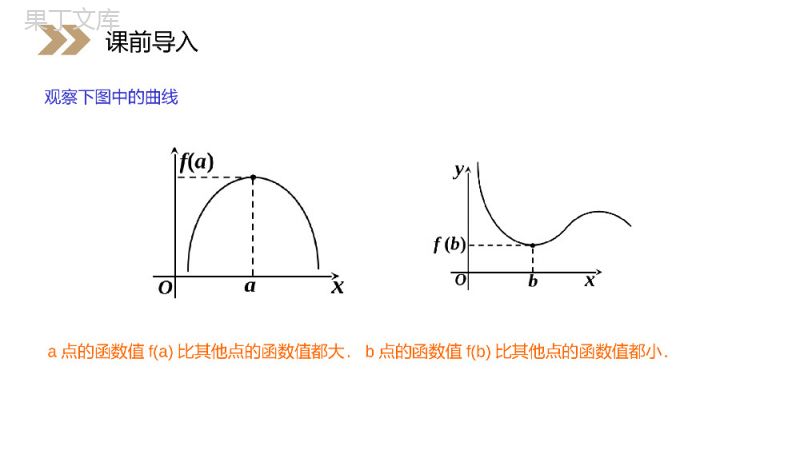
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-21.3.3函数的最大（小）值与导数第1章导数及其应用人教版高中数学选修2-2函数极值的定义——函数f(x)在点x0附近有定义，如果对x0附近的所有点都有f(x)f(x0)则f(x0)是函数f(x)的一个极小值.课前导入解方程.当时：'0fx'00fx（1）如果在附近的左侧，右侧，那么是极大值；0x0fx'0fx'0fx（2）如果在附近的左侧，右侧，那么是极小值；0x0fx'0fx'0fx课前导入'0fx'00fx0x0fx'0fx'0fx0x0fx'0fx'0fx观察下图，点a与点b处的函数值，与他们附近点的函数值有什么关系？ab)(bf)(af课前导入)(bf)(af观察下图中的曲线a点的函数值f(a)比其他点的函数值都大．b点的函数值f(b)比其他点的函数值都小．课前导入在某些问题中，往往关心的是函数在整个定义域区间上，哪个值最大或最小的问题，这就是我们通常所说的最值问题.课前导入观察右边一个定义在区间[a,b]上的函数y=f(x)的图象.发现图中____________是极小值，_________是极大值，在区间上的函数的最大值是______，最小值是_______.f(x1)、f(x3)f(x2)f(b)f(x3)xX2oaX3bx1y新知探究极值反映的是函数在某一点附近的局部性质，而不是函数在整个定义域的性质.但是，在解决实际问题或在研究函数性质时，往往更关心函数在某个区间上哪个值最大，哪个值最小？新知探究a1x2x3xo4x5x6xbxyxfy133.1图如下图，观察区间[a，b]上函数y=f(x)的图像，你能找出它的极大值﹑极小值吗？新知探究a1x2x3xo4x5x6xbxyxfy133.1图a1x2x3xo4x5x6xbxyxfy133.1图观察图像，可以发现是函数y=f(x)的极小值，是极大值.135fx,fx,fx246fx,fx,fx新知探究a1x2x3xo4x5x6xbxyxfy133.1图135fx,fx,fx246fx,fx,fx探究你能找出函数y=f(x)在区间[a，b]上的最大值﹑最小值吗？从图1.3-13可以看出，函数y=f(x)在区间[a，b]上的最大值是f(a)，最小值是.3fx新知探究3fxxfyabxyoa1x2x3xo4x5xbxyxfy143.1图153.1图在上图中，观察[a,b]上的函数y=f(x)的图像，它们在[a,b]上是否有最大值﹑最小值？如果有，分别是多少？新知探究xfyabxyoa1x2x3xo4x5xbxyxfy143.1图153.1图一般地，如果在区间[a,b]上函数y=f(x)的图像是一条连续不断的曲线，那么它必有最大值和最小值.新知探究如果在没有给出函数图象的情况下，怎样才能判断出最小值，最大值呢？把函数y=fx的所有极值连同端点的函数值进行比较,就可以求出函数的最大值与最小值.新知探究把函数y=fx的所有极值连同端点的函数值进行比较,就可以求出函数的最大值与最小值.求函数在[0,3]上的最大值与最小值.31fx=x-4x+43例题讲解42.33:4,0,3,x=2,fx=1x-4x+43f解由例可知在上当时f0=4,f3=1,又由于因此，函数f(x)在[0,3]上的最大值是4，最小值是.43有极小值，并且极小值为31fx=x-4x+4342.33:4,0,3,x=2,fx=1x-4x+43f解由例可知在上当时f0=4,f3=1,又由于43oxy234x4x31xf3163.1图上述结论可从函数f(x)在[0,3]上的图像得到直观的验证.例题讲解oxy234x4x31xf3163.1图求函数f(x)=x2-4x+6在区间[1，5]内的极值与最值..解:f’(x)=2x-4令f’(x)=0，即2x-4=0，得x=2.例题讲解x1（1，2）2（2，5）50y-+3112'y故函数f(x)在区间[1，5]内的极小值为3，最大值为11，最小值为.例题讲解'y求函数y=x4-2x2+5在区间[-2,2]上的最大值与最小值.例题讲解解:344.yxx令,解得x=-1，0，1.0y当x变化时,的变化情况如下表:,yyx-2(-2,-1)-1(-1,0)0(0,1)1(1,2)2y’-0+0-0+y13↘4↗5↘4↗13从上表可知,最大值是13,最小值是4.344.yxx0y,yy（1）极值是仅对某一点的附近而言，是在局部范围内讨论问题，而最值是对整个定义域而言，是在整体范围内讨论问题.极大（小）值与极大（小）值的区别是什么？例题讲解（2）函数在其定义域上的最大值与最小值至多各有一个，而函数的极值则可能不止一个，也可能没有极值,并且极大值（极小值）不一定就是最大值（最小值）.例题讲解一般地，求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下：（1）求函数y=f(x)在[a,b]内的极值；（2）将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较，其中最大的一个是最大值，最小的一个是最小值.知识要点求函数的最值时,应注意:闭区间[a,b]上的连续函数一定有最值.开区间(a,b)内的可导函数不一定有最值,但若有唯一的极值,则此极值必是函数的最值.+0－0+递增极大值递减极小值递增1、已知a≥0，函数f(x)=（-2ax）2xxe，当X为何值时，f(x)取得最小值？证明你的结论.解:对函数求导数得,f(x)2xf(x)=(x+2x-2ax-2a)e令解得f(x)=0,2212x=a-1-a+1,x=a-1+a+1当x变化时,f(x),f′(x)的变化如下表:课堂练习x),(1x1x),(21xx2x),(2x)(xf)(xf所以当时，f(x)取得最小值.112aax2xxef(x)2xf(x)=(x+2x-2ax-2a)ef(x)=0,2212x=a-1-a+1,x=a-1+a+1x),(1x1x),(21xx2x),(2x)(xf)(xf112aax1()21(0),fxxxx()fx2、设函数则A．有最大值B．有最小值C．是增函数D．是减函数B课堂练习（）1()21(0),fxxxx()fx1.已知f(x)=2x3-6x2+m（m为常数），在[-2,2]上有最大值3，函数在[-2,2]上的最小值_____.-372.函数f(x)=x3+ax+b，满足f(0)=0，且在x=1时取得极小值，则实数a的值为_____.-3课堂练习3.函数f(x)=x³-3x+1在闭区间[-3,0]上的最大值、最小值分别是（）A.1，－1B.1，-17C.3，-17D.9，-19C课堂练习4.函数f(x)的定义域为R，导函数f´(x)的图象如图，则函数f(x)（）A.无极大值点，有两个极小值点B.有三个极大值点，两个极小值点C.有两个极大值点，两个极小值点D.有四个极大值点，无极小值点Cxoy课堂练习5.求函数在区间[-1，3]上的最大值与最小值.22x-5x+6f(x)=x+1令,得解:2225(x-2x-1)f(x)=.(x+1)()0fx1212x=1-2,x=1+2,x,x[-1,3].且课堂练习相应的函数值为:7+527-52f(1-2)=,f(1+2)=.22又f(x)在区间端点的函数值为:f(-1)=6,f(3)=0比较得,f(x)在点处取得最大值在点处取得最小值1x=1-27+52;22x=1+27-52.222x-5x+6f(x)=x+12225(x-2x-1)f(x)=.(x+1)()0fx1212x=1-2,x=1+2,x,x[-1,3].且7+527-52f(1-2)=,f(1+2)=.221x=1-27+52;22x=1+27-52.2感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明一般地，求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下：（1）求函数y=f(x)在[a,b]内的极值；（2）将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较，其中最大的一个是最大值，最小的一个是最小值.课堂小结函数的极值是在局部范围内讨论问题，是一个局部概念，而函数的最值是对整个定义域而言，是在整体范围内讨论问题，是一个整体性的概念.讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-2感谢你的聆听第1章导数及其应用人教版高中数学选修2-2