《古典概型》人教版高中数学必修三PPT课件（第3.2.1课时）.pptx

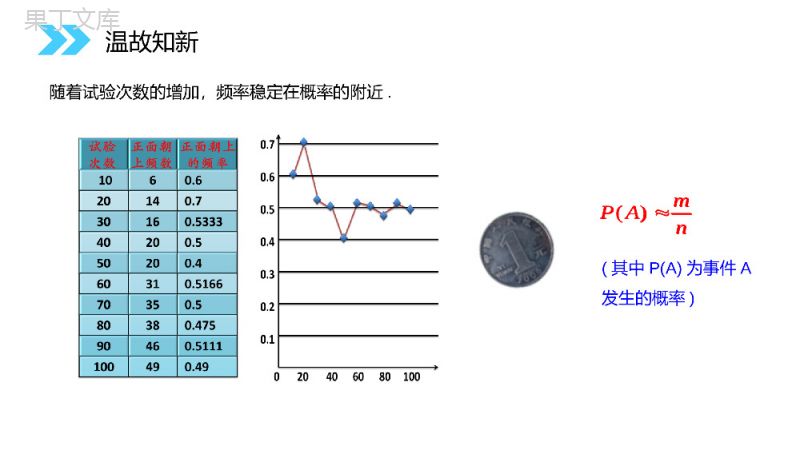
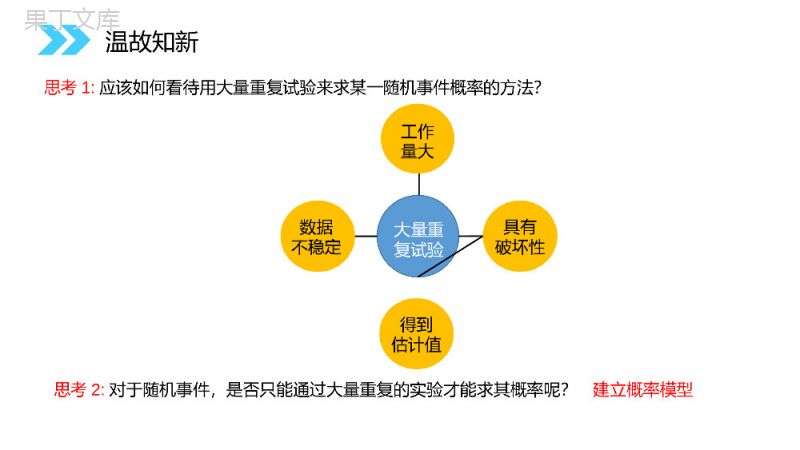
讲解人：办公资源时间：2020.6.1MENTALHEALTHCOUNSELINGPPT3.2.1古典概型第3章概率人教版高中数学必修3在几百年前的欧洲，一些国家的贵族们喜欢赌博，最常见的一种方式就是抛掷骰子来比较点数的大小。有的赌徒想到这样一个问题：假如同时抛两颗骰子，一种情况是出现的点数之和为5，另一种情况出现的点数之和为6，这两种情况，哪一种出现的可能性大一些呢？这是概率论历史上著名的德▪梅耳问题。情景设置1.概率的基本性质（1）、事件A的概率取值范围是（2）、如果事件A与事件B互斥，则（3）、若事件A与事件B互为对立事件，则P(A∪B)=P(A)=0≤P(A)≤1P(A)+P(B)1-P(B)温故知新nmAP)((其中P(A)为事件A发生的概率)随着试验次数的增加，频率稳定在概率的附近.温故知新nmAP)(工作量大大量重复试验数据不稳定具有破坏性得到估计值思考1:应该如何看待用大量重复试验来求某一随机事件概率的方法？思考2:对于随机事件，是否只能通过大量重复的实验才能求其概率呢？建立概率模型温故知新试验1:掷一枚质地均匀的硬币,观察可能出现哪几种结果？试验2:掷一枚质地均匀的骰子,观察可能出现的点数有哪几种结果？一次试验中可能出现的每一个结果称为一个基本事件探究新知基本事件的特点:思考3：(1)在一次试验中，会同时出现"1点"和"2点"这两个基本事件吗？(2)随机事件"出现点数小于3"与"出现点数大于3"包含哪几个基本事件？"4点""5点"和"6点"任何两个基本事件是互斥的任何事件(除不可能事件)都可以表示成基本事件的和不会"1点"和"2点"探究新知例1.从字母a、b、c、d任意取出两个不同字母的试验中，有哪些基本事件？{,}Aab{,}Bac{,}Cad{,}Dbc{,}Ebd{,}Fcd解：所求的基本事件共有6个：abcdbcdcd画树状图分析：为了解基本事件，我们可以按照某种顺序，把所有可能的结果都列出来。我们一般用列举法列出所有基本事件，画树状图是列举法的基本方法。探究新知一个袋中装有红、黄、蓝、绿四个大小形状完全相同的球，从中一次性摸出三个球，其中有多少个基本事件？解：所求的基本事件共有4个：A=,红、黄、蓝B=,红、黄、绿C=,红、蓝、绿D=.黄、蓝、绿黄蓝绿红红—蓝—绿黄—蓝—绿探究新知A=,红、黄、蓝B=,红、黄、绿C=,红、蓝、绿D=.黄、蓝、绿试验1:掷硬币试验2:掷骰子思考4:从基本事件角度来看,上述两个试验有何共同特征？有限相等(1)试验中所有可能出现的基本事件的个数(2)每个基本事件出现的可能性有限性等可能性我们将具有这两个特点的概率模型称为古典概率模型，简称古典概型探究新知思考5:下列两个模型是古典概型吗？(1)向一个圆面内随机地投射一个点,如果该点落在圆内任意一点都是等可能的,你认为这一试验能用古典概型来描述吗?为什么？①有限性②等可能性×??探究新知思考5:下列两个模型是古典概型吗？(2)某同学随机地向一靶心进行射击，这一试验的结果只有有限个：“命中10环”、“命中9环”、“命中8环”、“命中7环”、“命中6环”、“命中5环”和“不中环”。你认为这是古典概型吗？为什么？①有限性②等可能性×??1099998888777766665555探究新知思考6:古典概型下,每个基本事件出现的概率是多少?随机事件出现的概率又如何计算？试验1:掷硬币（“2点”）P（“4点”）P（“3点”）P（“5点”）P（“6点”）P(1)基本事件的概率试验2:掷骰子古典概型中,若基本事件总数有n个,则每一个基本事件出现的概率都为（"反面向上"）Px由概率的加法公式：x+x=121因此x=x61因此x=由概率的加法公式：6x=1("正面向上"）P（“1点”）P探究新知(2)随机事件的概率分析:基本事件总数为：61点，2点，3点，4点，5点，6点记事件A为"出现点数小于3",事件B为"出现点数大于3"试验2:掷骰子事件A包含2个基本事件:1点,2点=P(4点)+P(5点)+P(6点)===（B）P16161663事件B包含3个基本事件:4点,5点,6点21=P(1点)+P(2点)===（A）P16166231探究新知古典概型的概率计算公式：111m=nPAnnn个mA包含的基本事件的个数P(A)＝基本事件的总数基本事件的总数为n,事件A包含的基本事件个数为m,P(A)=?探究新知111m=nPAnnn个mA包含的基本事件的个数P(A)＝基本事件的总数例2.单选题是标准化考试中常用的题型，一般是从A，B，C，D四个选项中选择一个正确答案。假设考生不会做，他随机的选择一个答案，问他答对的概率是多少？解：基本事件共4个:选A,选B,选C,选D,正确答案只有1个。设事件A为“选中的答案正确”，从而由古典概型的概率计算公式得：41)(＝基本事件的总数的基本事件的个数事件AAP实战演练变式：在标准化的考试中既有单选题又有不定项选择题，不定项选择题是从A,B,C,D四个选项中选出所有正确的答案，假设考生不会做，他随机的选择一个答案，问他答对的概率是多少？151)(“答对”P解；基本事件共15个：(A),(B),(C),(D),(AB)(AC)(AD)(BC)(BD)(CD)(ABC)(ABD)(ACD)(BCD)(ABCD)正确答案只有1个。由古典概型概率公式得实战演练古典概型解题思路：①验证试验是否符合古典概型；②设事件为A，确定基本事件总数n；确定事件A包含的基本事件个数m；③用古典概型公式进行计算.实战演练十一期间，商场为了促销,组织摸奖活动。游戏规则:盒中有大小均匀,编号为1、2、3的红球和编号为4、5的蓝球。要求：一次摸两球,一等奖:二等奖:练习.3个红球2个蓝球13245(1)依据以下两个方案，应如何设置一、二等奖？方案2:方案1:摸到两个蓝球摸到一红一蓝且号码和为偶数的两个小球实战演练游戏规则:盒中有大小均匀,编号为1、2、3的红球和编号为4、5的蓝球。要求：一次摸两球,方案2:方案1:摸到两个蓝球摸到一红一蓝且号码和为偶数的两个小球解：记事件A为“摸到两个蓝球”基本事件总数为：10分别为（1，2）、（1，3）（1，4）（1，5)（2，3）、（2，4）（2，5）、（3，4）、（3，5）、（4，5)事件A包含（4，5）,事件B包含（1，5）、（3，5）、（2，4）所以P(A)=P(B)=101103事件B为“摸到一红一蓝且号码和为偶数的两个小球”实战演练101103解记事件C为不中奖事件方法一：P(C)=1-(p(A)+P(B))=方法二：事件C包含基本事件6个，（1，2）、（1，4）、（2，3）、（2，5）、（3，4）（3，5）、（4，5）所以P(C)=(2)求不中奖的概率？5353实战演练5353思考7：要不要将两个骰子标上记号？如果不标记号会出现什么情况？你能解释其中的原因吗？如果不标上记号，类似于（3，6）和（6，3）的结果将没有区别。实战演练如果不标上记号，类似于（3，6）和（6，3）的结果将没有区别。（6，6）（6，5）（6，4）（6，3）（6，2）（6，1）（5，6）（5，5）（5，4）（5，3）（5，2）（5，1）（4，6）（4，5）（4，4）（4，3）（4，2）（4，1）（3，6）（3，5）（3，4）（3，3）（3，2）（3，1）（2，6）（2，5）（2，4）（2，3）（2，2）（2，1）（1，6）（1，5）（1，4）（1，3）（1，2）（1，1）6543216543211号骰子2号骰子思考7：要不要将两个骰子标上记号？如果不标记号会出现什么情况？你能解释其中的原因吗？实战演练（6，6）（6，5）（6，4）（6，3）（6，2）（6，1）（5，6）（5，5）（5，4）（5，3）（5，2）（5，1）（4，6）（4，5）（4，4）（4，3）（4，2）（4，1）（3，6）（3，5）（3，4）（3，3）（3，2）（3，1）（2，6）（2，5）（2，4）（2，3）（2，2）（2，1）（1，6）（1，5）（1，4）（1，3）（1，2）（1，1）（4，1）（3，2）（2，3）（1，4）6543216543211号骰子2号骰子（2）在上面的结果中，向上的点数之和为5的结果有4种，分别为：（1，4）,（2，3）,（3，2）,（4，1）。A41A369所包含的基本事件的个数（）＝＝＝基本事件的总数P由于所有36种结果是等可能的，其中向上点数之和为5的结果（记为事件A）有4种，则从表中可以看出同时掷两个骰子的结果共有36种。实战演练A41A369所包含的基本事件的个数（）＝＝＝基本事件的总数P(2)古典概型的特点:(3)古典概型计算任何事件A的概率计算公式:(1)基本事件的两个特点：①任何两个基本事件是互斥的；①有限性；②等可能性。②任何事件(除不可能事件)都可以表示成基本事件的和。(4)数学思想方法:特殊到一般课堂小结1.(必做题)课本130页：1,2,32.(选做题)设有关于x的一元二次方程bx+2ax+b=0,若a,b是从0,1,2,3四个数中任意选取的两个数,求上述方程有两个相异实根的概率？作业感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明讲解人：办公资源时间：2020.6.1MENTALHEALTHCOUNSELINGPPT感谢你的聆听第3章概率人教版高中数学必修3