中考专题：隐形圆在解题中的应用

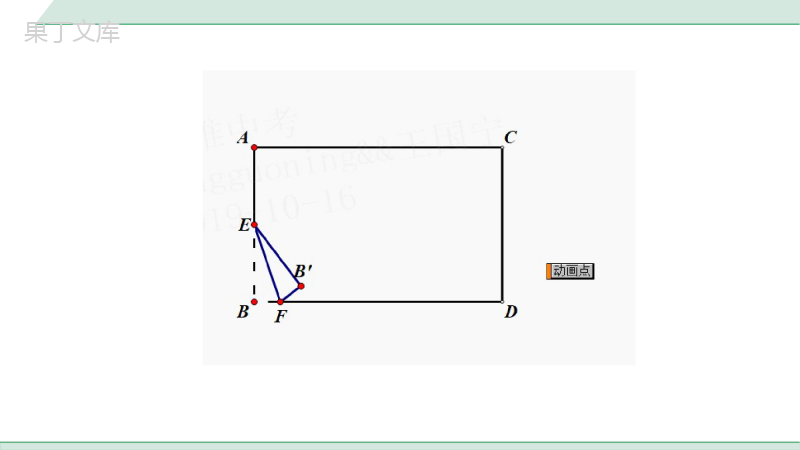
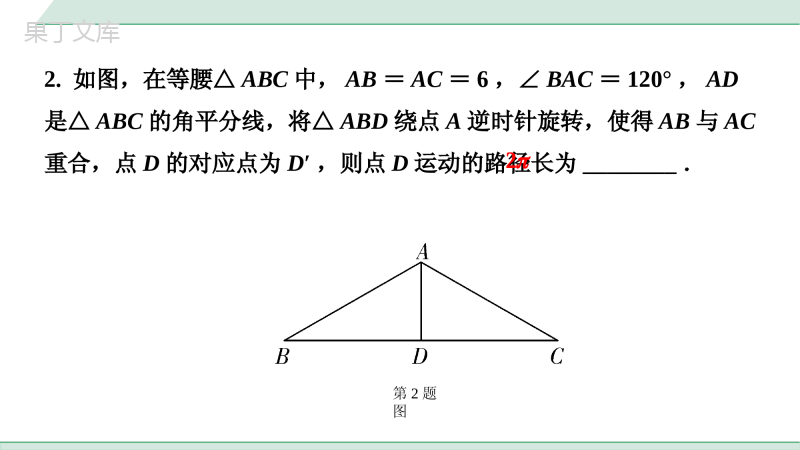
微专题隐形圆在解题中的应用已知平面内一定点A和一动点B，若AB长度固定，则动点B的轨迹是以点A为圆心，AB长为半径的圆(如图)(依据的是圆的定义，圆是所有到定点的距离等于定长的点的集合)．模型一定点定长作圆(2012～2019.15)推广：在折叠或旋转问题中，有时会利用“定点定长作圆”模型确定动点的运动轨迹．模型分析1.如图，在矩形ABCD中，AB＝4，AD＝2，E是AB的中点，F是AD边上的一个动点，将△AEF沿EF折叠，得到△GEF，点A的对应点为点G，则当点F沿AD边从点A运动到点D时，点G的运动路径长为_____．第1题图模型应用4334332.如图，在等腰△ABC中，AB＝AC＝6，∠BAC＝120°，AD是△ABC的角平分线，将△ABD绕点A逆时针旋转，使得AB与AC重合，点D的对应点为D′，则点D运动的路径长为________．第2题图22已知平面内一定点D和⊙O，点E是⊙O上一动点，设点O与点D之间距离为d，⊙O半径为r.模型二点圆最值(2017.22)位置关系点D在⊙O内点D在⊙O上点D在⊙O内外图示DE的最大值d＋r2rd＋r模型分析位置关系点D在⊙O内点D在⊙O上点D在⊙O内外此时点E的位置连接DO并延长交⊙O于点EDE的最小值r－d0d－r此时点E的位置连接OD并延长交⊙O于点E点E与点D重合连接OD交⊙O于点E【应用依据】直径是圆中最长的弦．3.已知，OC＝5，点A、B分别是平面内的动点，且OA＝4，BC＝3，点A、B的运动轨迹如图所示，则OB长的最大值为______，OB长的最小值为______，AC长的最大值为______，AC长的最小值为________，AB长的最大值为________，AB长的最小值为________．第3题图模型应用82911204.已知PA、PB分别与⊙O相切于点A，B，⊙O的半径为3，∠APB＝60°，点C在⊙O上运动，则PC长的最大值为________．第4题图9位置关系直线与⊙O相离直线与⊙O相切直线与⊙O相交图示点Q到直线l距离的最大值d＋r2rd＋r模型三线圆最值已知⊙O及直线l，⊙O的半径为r，点Q为⊙O上一动点，圆心O与直线l之间的距离为d.模型分析位置关系直线与⊙O相离直线与⊙O相切直线与⊙O相交此时点Q的位置过点O作直线l的垂线，其反向延长线与⊙O的交点，即为点Q点Q到直线l距离的最小值d－r00此时点Q的位置过点O作直线l的垂线，与⊙O的交点即为点Q直线l与⊙O的交点即为点Q推广：在解决某些面积最值问题时，常利用此模型，将问题转化为求动点到定边的最大(小)距离，进而利用面积公式求解．5.如图，已知AB＝4，∠APB＝90°，则△APB面积的最大值为_______．6.如图，在边长为2的菱形ABCD中，∠A＝60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′B，A′C，则△A′BC面积的最小值为________．第6题图第5题图模型应用43131如图，△ABC中，∠C＝90°，点C为动点，则点C的轨迹是以AB为直径的⊙O(不包含A、B两点)．模型四直角对直径(2014.22)注：作出辅助圆是关键，计算时结合求点圆、线圆最值等方法进行相关计算．模型分析7.如图，在Rt△ABC中，AB⊥BC，AB＝6，BC＝4，P是△ABC内部的一个动点，且满足∠PAB＝∠PBC，连接CP，则CP长的最小值为()A.B.2C.D.第7题图81313121313模型应用32B81313121313328.如图，正方形ABCD的边长为4，点E是AB边上的一个动点，点F是CD边上的一个动点，且AE＝CF，过点B作BG⊥EF于点G，连接AG，则AG长的最小值为________．第8题图1021021.如图①，在四边形ABCD中，∠ADC＝∠ABC＝90°.如图②，在四边形ABDC中，∠ADC＝∠ABC＝90°.结论：(1)点A、B、C、D在同一个圆上；(2)AC为四边形ABDC的外接圆的直径．图①图②模型分析模型五四点共圆2.如图③，AB为△ABC和△ABD的公共边，且点C、D在AB的同侧，∠C＝∠D.图③结论：点A、B、C、D在同一个圆上．9.如图，在△ABC中，三条高AD、BE、CF相交于点H，连接DE、DF，若∠BAC＝64°，则∠EDF的度数为________．10.如图，在等边△ABC中，AB＝6，P为AB上一动点，过点P作PD⊥BC，PE⊥AC，则DE的最小值为________．第9题图第10题图模型应用52°9292第11题图11.如图，在△ABC中，∠ACB＝90°，AC＝4，BC＝3，∠CPB＝∠A，过点C作CP的垂线，与PB的延长线交于点Q，求CQ的最大值．∵∠CPB＝∠A，∠ACB＝90°，∴A、P、B、C四点共圆，圆心为AB的中点O，且AB为⊙O的直径，∴点P在⊙O上运动，解：如解图，O∵∠ACB＝∠PCQ＝90°，∠A＝∠CPB，∴△ABC∽△PQC，∴，∴CQ＝PC，要使得CQ最大，只需PC最大，当PC为⊙O的直径时，PC取得最大值，∵AC＝4，BC＝3，∴AB＝5，∴PC的最大值为5，∴CQ的最大值为.34BCQCACPC34第11题图O15434BCQCACPC34154