分式的加减第2课时(异分母)-2022-2023学年八年级数学上册同步教材配套精品教学课件(人教版)

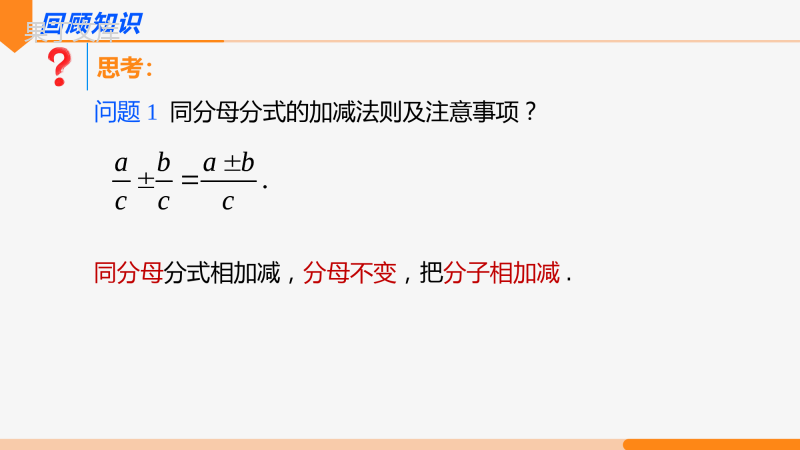
第十五章分式异分母的分式相加减15.2.2分式的加减第2课时回顾知识思考：问题1同分母分式的加减法则及注意事项？同分母分式相加减，分母不变，把分子相加减..ababccc.ababccc1计算:(1)解：原式=2222532.xyxxyxy2222532xyxxyxy22532xyxxy2233xyxy3.xy2222(1);44xyxyxyxy2222()()(1)4xyxyxy原式224yxy22224xyxyxy;2yx(2)原式=2222532.xyxxyxy2222532xyxxyxy22532xyxxy2233xyxy3.xy2222(1);44xyxyxyxy2222()()(1)4xyxyxy原式224yxy22224xyxyxy;2yx探究新知思考：问题2类比分数的加减计算下列各式：归纳：说一说异分母的分式应该如何加减?31216236562633121626362361ba11abbaabaabbba11abb-aaba-abb31216236562633121626362361ba11abbaabaabbba11abb-aaba-abb归纳知识异分母分式的加减法则异分母分式相加减，先通分，变同分母的分式，再加减..acadbcadbcbdbdbdbd.acadbcadbcbdbdbdbd典例讲解2111xxx（1）；例1计算：112323pqpq（2）；2221(3).244xxxxxx2111xxx（1）；112323pqpq（2）；2221(3).244xxxxxx典例讲解2111xxx（1）；解：原式=2111xxx=2(1)1xx例1计算：31xx；=112323pqpq（2）；解：原式=2323(23)(23)(23)(23)pqpqpqpqpqpq(23)(23)(23)(23)pqpqpqpq4(23)(23)ppqpq22449ppq；2111xxx（1）；2111xxx2(1)1xx31xx；112323pqpq（2）；2323(23)(23)(23)(23)pqpqpqpqpqpq(23)(23)(23)(23)pqpqpqpq4(23)(23)ppqpq22449ppq；2221(3).244xxxxxx解：原式=221(2)(2)xxxxx=22(2)(2)(1)(2)(2)xxxxxxxx=2224(2)xxxxx=24.(2)xxx2221(3).244xxxxxx221(2)(2)xxxxx22(2)(2)(1)(2)(2)xxxxxxxx2224(2)xxxxx24.(2)xxx例2计算：211aaa法一：原式=2(1)(1)11aaaaa22(1)1aaa2211aaa11a法二：原式=2(1)1aaa2(1)1111aaaaaaa22()(1)1aaaaa2211aaaaa11a2(1)(1)1aaaaa211aaa2(1)(1)11aaaaa22(1)1aaa2211aaa11a2(1)1aaa2(1)1111aaaaaaa22()(1)1aaaaa2211aaaaa11a2(1)(1)1aaaaa例3化简22193mmm从1、-3、3中任选一个你喜欢的m值代入求值.2333mmmm（）解：原式当m=1时，原式333mmm1.-3m11-31.2233333mmmmmm22193mmm2333mmmm（）333mmm1.-3m11-31.2233333mmmmmm课堂小结通分异分母相加减同分母相加减分子相加减分母不变最简分式约分转化转化分式的加减法的思路课堂小结分式的加减同分母异分母分数类比同分母分式相加减，分母不变，把分子相加减..ababccc异分母分式相加减，先通分，变同分母的分式，再加减..acadbcadbcbdbdbdbd.ababccc.acadbcadbcbdbdbdbd课堂练习1.计算的结果是()A.B.C.D.a+baba2()ababaabbaaabaA2.计算的结果（）A.B.C.D.22222aabbbababbabaabbabAabaaba2()ababaabbaaaba22222aabbbababbabaabbababa4.计算：233(2).11xxx222(1);xyxxyxy22(1)(2).1xxxyx；3.已知两个式子：其中x≠±2，则A与B的关系是()A．相等B．互为倒数C．互为相反数D．A大于B2411,,422ABxxxC233(2).11xxx222(1);xyxxyxy22(1)(2).1xxxyx；2411,,422ABxxx221(1);42xxx2116(2).3629xxxx22(1)=(+2)(2)(+2)(2)xxxxxx原式2(+2)(+2)(2)xxxx21;(+2)(2)2xxxx116(2)=32(3)(3)(3)xxxxx原式2(3)2(3)(3)xxx2(69)2(3)(3)xxxx2(3)(1)(3)122(3)(3)xxxxx3.26xx5.计算：221(1);42xxx2116(2).3629xxxx22(1)=(+2)(2)(+2)(2)xxxxxx原式2(+2)(+2)(2)xxxx21;(+2)(2)2xxxx116(2)=32(3)(3)(3)xxxxx原式2(3)2(3)(3)xxx2(69)2(3)(3)xxxx2(3)(1)(3)122(3)(3)xxxxx3.26xx