24-5-三角形的内切圆-2022-2023学年九年级数学下册同步教学课件(沪科版)

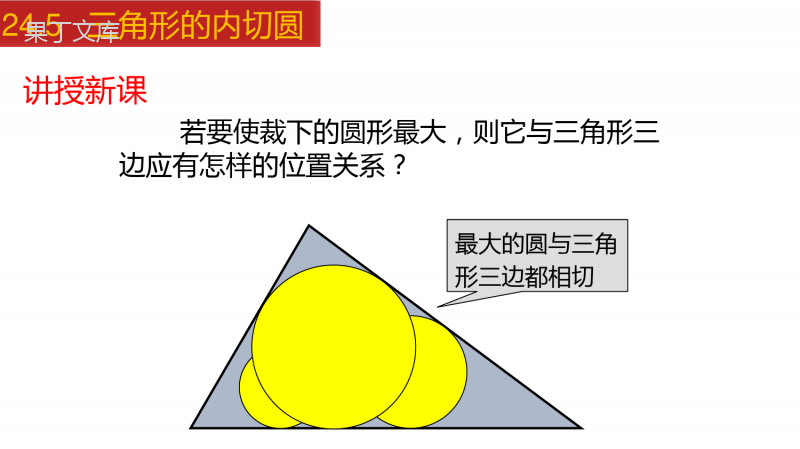
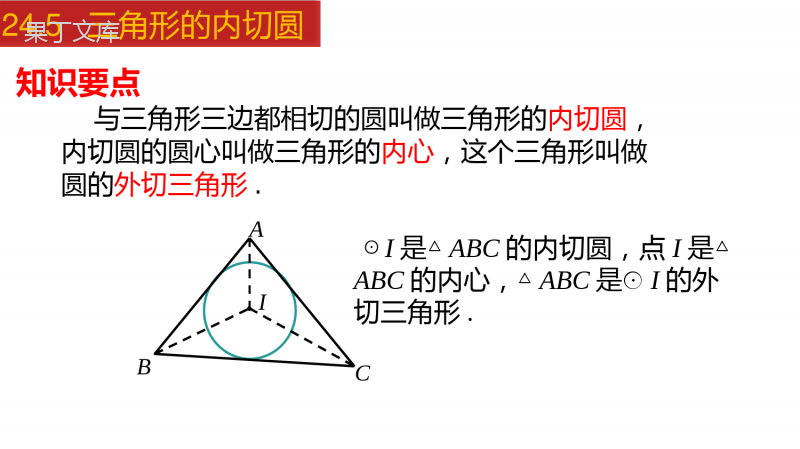
三角形的内切圆24.5三角形的内切圆学习目标1.了解有关三角形的内切圆和三角形的内心的概念.2.掌握三角形内心的性质并能加以应用.3.学会利用方程思想解决几何问题，体验数形结合思想.24.5三角形的内切圆有一块三角形材料，如何从中裁下一个面积最大的圆？情境引入24.5三角形的内切圆讲授新课若要使裁下的圆形最大，则它与三角形三边应有怎样的位置关系？最大的圆与三角形三边都相切24.5三角形的内切圆与三角形三边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形.BACI知识要点☉I是△ABC的内切圆，点I是△ABC的内心，△ABC是☉I的外切三角形.24.5三角形的内切圆问题1如图，若⊙O与∠ABC的两边相切，那么圆心O的位置有什么特点？圆心O在∠ABC的平分线上.NCOMAB探究24.5三角形的内切圆COAB问题2如图，如果⊙O与△ABC的内角∠ABC的两边相切，且与内角∠ACB的两边也相切，那么此⊙O的圆心在什么位置？圆心O在∠ABC与∠ACB这两个角的平分线的交点上.线段AO，BO，CO分别是∠BAC，∠ABC，∠ACB的平分线.FED线段线段OD，OE，OF的长度相等，等于三角形内切圆的半径.24.5三角形的内切圆1.如图，作ΔABC中∠A，∠C的角平分线，交于点O问题3现在你知道如何画△ABC的内切圆了吗？???????2.过点O作OQ⊥AC于Q3.以O点为圆心，OQ长度为半径画圆则☉O即为所求求作一个圆，使它和已知三角形的各边相切24.5三角形的内切圆三角形内心的性质：三角形的内心在三角形的角平分线上.三角形的内心到三角形的三边距离相等.COABFED知识归纳24.5三角形的内切圆名称确定方法图形性质外心：三角形外接圆的圆心内心：三角形内切圆三角形三边垂直平分线的交点1.OA=OB=OC2.不一定在三角形内部三角形三条角平分线的交点1.到三边距离相等2.AO、BO、CO分别平分∠BAC、∠ABC、∠ACBABOCABCO类比归纳24.5三角形的内切圆例1如图，△ABC中，∠ABC=43°，∠ACB=61°，点I是△ABC的内心，求∠BIC的度数.解：连接IB，IC.ABCI∵点I是△ABC的内心，∴BI，CI分别是∠ABC，∠ACB的平分线.在△IBC中，128)6243(21180)(180)(180CBICBIBCBIC24.5三角形的内切圆128)6243(21180)(180)(180CBICBIBCBIC例2如图，一个木模的上部是圆柱，下部是底面为等边三角形的直三棱柱.圆柱的下底面圆是直三棱柱上底面等边三角形的内切圆，已知直三棱柱的底面等边三角形的边长为3cm，求圆柱底面圆的半径.该问题可以抽象为如下所示的几何图形.24.5三角形的内切圆CABrOD解：如图，设圆O切AB于点D，连接OA、OB、OD.∵圆O是等边△ABC的内切圆，∴AO、BO是∠BAC、∠ABC的平分线.∴∠OAB=∠OBA=30°.∵OD⊥AB，AB=3cm，∴AD=BD=AB=1.5(cm).12∴OD=AD·tan30°=(cm).32答：圆柱底面圆的半径为cm.3224.5三角形的内切圆123232例3△ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F，且AB=13cm，BC=14cm，CA=9cm，求AF、BD、CE的长.想一想：图中你能找出哪些相等的线段？理由是什么？BACEDFO24.5三角形的内切圆解:设AF=xcm，则AE=xcm.∴CE=CD=AC-AE=9-x(cm)，BF=BD=AB-AF=13-x(cm).由BD+CD=BC，可得(13-x)+(9-x)=14，∴AF=4cm，BD=9cm，CE=5cm.方法小结：关键是熟练运用切线长定理，将相等线段转化集中到某条边上，从而建立方程求解.解得x=4.BACEDFO24.5三角形的内切圆例4如图所示，⊙O是Rt△ABC的内切圆，切点分别为D，E，F，∠C＝90°，AC＝3，BC＝4，求⊙O的半径r.连接OA，OB，OC，OD，OE，OF，利用S△ABC＝S△COB＋S△BOA＋S△AOC求解．还可以发现四边形OECD为正方形，则可利用切线长定理，用含r的代数式表示AB的长，再求分析：24.5三角形的内切圆方法一：如图，连接OA，OB，OC，OD，OE，OF，则OD＝OE＝OF＝r，OD⊥BC，OE⊥AC，OF⊥AB.在Rt△ABC中，AB＝∵S△ABC＝S△COB＋S△BOA＋S△AOC，∴∴r＝2222345.ACBC11112222ACBCBCrABrACr341.453ACBCBCABAC解：1().2BCABACr24.5三角形的内切圆2222345.ACBC11112222ACBCBCrABrACr341.453ACBCBCABAC1().2BCABACr方法二：如图，连接OD，OE，则OE⊥AC，OD⊥BC，又∵EC⊥CD，且OE＝OD＝r，∴四边形OECD是正方形．∴EC＝CD＝r.∴AB＝AF＋BF＝AE＋BD＝(AC－EC)＋(BC－CD)＝3－r＋4－r＝7－2r.又易知AB＝2222345,ACBC24.5三角形的内切圆2222345,ACBC当堂练习（3）若∠BIC=100°，则∠A=度.（2）若∠A=80°，则∠BIC=度.130201.如图，在△ABC中，点I是内心，（1）若∠ABC=50°，∠ACB=70°，∠BIC=_____.ABCI120°24.5三角形的内切圆2.在Rt△ABC中，∠C＝90°，AC＝3，AB＝5，则它的内切圆与外接圆半径分别为()A．1.5，2.5B．2，5C．1，2.5D．2，2.53.如图，正三角形ABC的内切圆半径为1，那么这个正三角形的边长为()A．2B．3C.D．233DC24.5三角形的内切圆33ABCOcDEr4.如图，直角三角形的两直角边分别是a、b,斜边为c，则其内切圆的半径r为___________（以含a、b、c的代数式表示r）.2abcr+-=解析：如图，过点O分别作AC，BC，AB的垂线，垂足分别为D，E，F.F则AD=AC-DC=b-r,BE=BC-CE=a-r,因为AF=AD，BF=BE，AF+BF=c,所以a-r+b-r=c,所以.2abcr+-=ba24.5三角形的内切圆2abcr+-=.2abcr+-=CABOD5.求边长为6cm的等边三角形的内切圆半径与外接圆半径.解：如图，由题意可知BC=6cm,∠ABC=60°，OD⊥BC，BO平分∠ABC.∴∠OBD=30°，BD=3cm,△OBD为直角三角形.tan303cm.ODBD==∴内切圆半径外接圆半径23cm.cos30BDOB==24.5三角形的内切圆tan303cm.ODBD==∴23cm.cos30BDOB==6.△ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F，且AB=13cm，BC=14cm，CA=9cm，求AF、BD、CE的长.BACEDFO解:设AF=xcm，则AE=xcm.∴CE=CD=AC-AE=9-x(cm)，BF=BD=AB-AF=13-x(cm).由BD+CD=BC，可得(13-x)+(9-x)=14，∴AF=4cm，BD=9cm，CE=5cm.解得x=4.24.5三角形的内切圆三角形内切圆运用切线长定理，将相等线段转化集中到某条边上，从而建立方程求解.有关概念内心概念及性质应用课堂小结24.5三角形的内切圆THANKS“”24.5三角形的内切圆