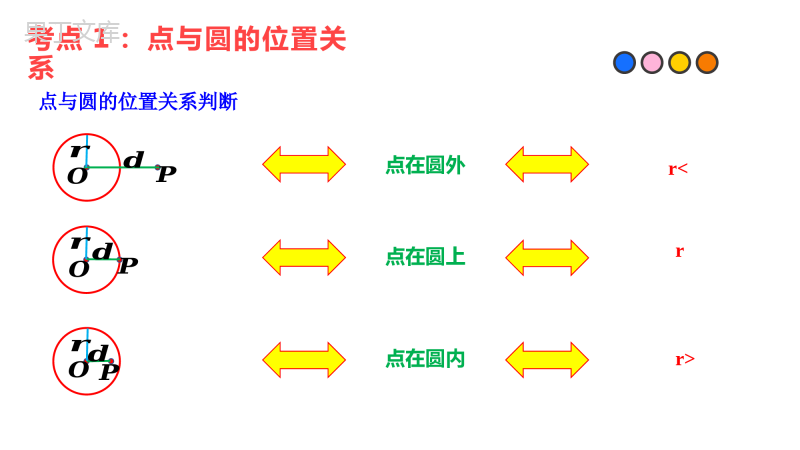
专题15-与圆有关的位置关系(课件)2023年中考数学一轮复习(全国通用)

专题15与圆有关的位置关系备战2023年数学中考一轮复习MarketingPlanningLOGO考点1：点与圆的位置关系点与圆的位置关系判断????????????r点在圆外点在圆上点在圆内考点1：点与圆的位置关系确定圆的条件?????不在同一直线上的3个点确定一个圆。反证法:假设命题的结论不成立,由此经过推理得出矛盾，由矛盾断定所作假设不正确，从而得到原命题成立.反证法证明问题的3个步骤:①假设;②推理；③结论.考点1：点与圆的位置关系三角形的外接圆?????定义:经过三角形的3个顶点可以作一个圆,这个圆叫作三角形的外接圆；外接圆的圆心是三角形3条边的垂直平分线的交点,叫作这个三角形的外心。拓展:①三角形的外心是三角形3条边的垂直平分线的交点；②任意三角形有且只有1个外接圆；③锐角三角形的外心在其内部，直角三角形的外心是其斜边的中点，钝角三角形的外心在其外部。考点1：点与圆的位置关系三角形外接圆的作法:?????确定圆心：三角形两条边的垂直平分线的交点即为三角形的外心。确定半径：交点和三角形任意一顶点的距离即为外接圆的半径长。????例1．在直角坐标系中，如果⊙O是以原点0,0O为圆心，以10为半径的圆，那么点8,6A的位置（）A．在⊙O内B．在⊙O外C．在⊙O上D．不能确定【答案】C【分析】根据两点间的距离公式求出AO的长，然后与⊙O的半径比较，即可确定点A的位置．【详解】解：∵点8,6A﹣，∴266810AO，∴点A在⊙O上，故选：C．【点拨】此题考查了点与圆的位置关系，解题的关键是要记住若半径为r，点到圆心的距离为d，则有：当dr>时，点在圆外；当dr时，点在圆上；当dr时，点在圆内．例1．在直角坐标系中，如果⊙O是以原点0,0O为圆心，以10为半径的圆，那么点8,6A的位置（）A．在⊙O内B．在⊙O外C．在⊙O上D．不能确定【答案】C【分析】根据两点间的距离公式求出AO的长，然后与⊙O的半径比较，即可确定点A的位置．【详解】解：∵点8,6A﹣，∴266810AO，∴点A在⊙O上，故选：C．【点拨】此题考查了点与圆的位置关系，解题的关键是要记住若半径为r，点到圆心的距离为d，则有：当dr>时，点在圆外；当dr时，点在圆上；当dr时，点在圆内．例2．下列说法正确的是（）A．三个点确定一个圆B．当点P到圆心的距离小于半径时，点P在圆外C．边长为R的正六边形的边心距等于32RD．圆心角相等，它们所对的弧相等【答案】C【分析】分别根据确定圆的条件，点与圆的位置关系，圆心角、弧、弦的关系及圆内接正六边形的性质对各选项进行逐一判断．【详解】解：A、只有不在同一条直线上的三点才可以确定一个圆，故错误，不合题意；B、当点P到圆心的距离小于半径时，点P在圆内，故错误，不合题意；C、边长为R的正六边形的边心距等于221322RRR，故正确，符合题意；D、只有在同圆或等圆中圆心角相等，它们所对的弧相等，故错误，不合题意；故选：C．【点拨】本题考查的是确定圆的条件，点与圆的位置关系，圆心角、弧、弦的关系及圆内接正六边形的性质，熟练掌握以上知识是解答此题的关键．例2．下列说法正确的是（）A．三个点确定一个圆B．当点P到圆心的距离小于半径时，点P在圆外C．边长为R的正六边形的边心距等于32RD．圆心角相等，它们所对的弧相等【答案】C【分析】分别根据确定圆的条件，点与圆的位置关系，圆心角、弧、弦的关系及圆内接正六边形的性质对各选项进行逐一判断．【详解】解：A、只有不在同一条直线上的三点才可以确定一个圆，故错误，不合题意；B、当点P到圆心的距离小于半径时，点P在圆内，故错误，不合题意；C、边长为R的正六边形的边心距等于221322RRR，故正确，符合题意；D、只有在同圆或等圆中圆心角相等，它们所对的弧相等，故错误，不合题意；故选：C．【点拨】本题考查的是确定圆的条件，点与圆的位置关系，圆心角、弧、弦的关系及圆内接正六边形的性质，熟练掌握以上知识是解答此题的关键．例3．有下列说法：①任意三点确定一个圆；②圆的两条平行弦所夹的弧相等；③任意一个三角形有且仅有一个外接圆；④平分弦的直径垂直于弦；⑤直径是圆中最长的弦，其中错误的个数有（）A．2个B．3个C．4个D．5个【答案】A【分析】根据圆的确定条件，圆心角、弧、弦的关系，三角形的外接圆的定义，垂径定理逐项判断即可．【详解】解：不在同一直线上的三点确定一个圆，故①错误；圆的两条平行弦所夹的弧相等，故②正确；任意一个三角形有且仅有一个外接圆，故③正确；平分弦（非直径）的直径垂直于弦，故④错误；直径是圆中最长的弦，故⑤正确．综上可知错误的个数有2个．故选A．【点拨】本题考查圆的确定条件、垂径定理、圆心角、弧、弦的关系等知识，解题关键是熟记相关知识点，准确进行判断．例3．有下列说法：①任意三点确定一个圆；②圆的两条平行弦所夹的弧相等；③任意一个三角形有且仅有一个外接圆；④平分弦的直径垂直于弦；⑤直径是圆中最长的弦，其中错误的个数有（）A．2个B．3个C．4个D．5个【答案】A【分析】根据圆的确定条件，圆心角、弧、弦的关系，三角形的外接圆的定义，垂径定理逐项判断即可．【详解】解：不在同一直线上的三点确定一个圆，故①错误；圆的两条平行弦所夹的弧相等，故②正确；任意一个三角形有且仅有一个外接圆，故③正确；平分弦（非直径）的直径垂直于弦，故④错误；直径是圆中最长的弦，故⑤正确．综上可知错误的个数有2个．故选A．【点拨】本题考查圆的确定条件、垂径定理、圆心角、弧、弦的关系等知识，解题关键是熟记相关知识点，准确进行判断．考点2：直线与圆的位置关系直线与圆的位置关系相关概念相交:直线和圆有两个公共点,这时我们说这条直线和圆相交，这条直线叫作圆的割线相切:直线和圆只有1个公共点,这时我们说这条直线和圆相切，这条直线叫作圆的切线，这个点叫作切点。相离:直线和圆没有公共点,这时我们说这条直线和圆相离。考点2：直线与圆的位置关系点与圆的位置关系判断????????????r相离相切相交考点2：直线与圆的位置关系切线的判定切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。拓展：在判定直线与圆相切时，若直线与圆的公共点已知，证明方法是“连半径，证垂直，得切线”；若直线与圆的公共点未知，证明方法是“作垂线段,证d=r,得切线”.?????考点2：直线与圆的位置关系切线的性质切线的性质:圆的切线垂直于过切点的半径。切线长:从圆外一点作圆的切线,这一点和切点之间的线段的长度叫作切线长。?????切线长定理:从圆外一点作圆的两条切线,它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.如图,PA,PB是⊙O的两条切线,切点分别为A,B,则PA=PB,OPA∠=OPB∠.考点2：直线与圆的位置关系三角形的内切圆定义:与三角形各边都相切的圆叫作三角形的内切圆,内切圆的圆心是三角形3条角平分线的交点，叫作三角形的内心。拓展:①三角形的内心是三角形3条内角平分线的交点.②任意三角形有且只有一个内切圆，内心一定在三角形内.?????考点2：直线与圆的位置关系三角形的内切圆的作法①确定圆心：三角形两条角平分线的交点即为三角形的内心。拓展:若三角形三边的边长分别为a,b,c,内切圆的半径为r,则三角形的面积为:。?????②确定半径：交点到三角形任意一边的距离即为内切圆的半径长。???例4．已知O的半径为3，圆心O到直线AB的距离为5，则直线AB与O的位置关系（）A．相交B．相切C．相离D．相交或相切【答案】C【分析】根据O的半径为3，圆心O到直线AB的距离为5得3r，5d，可得rd，即可得．【详解】解：∵O的半径为3，圆心O到直线AB的距离为5，∴3r，5d，∴rd，∴直线AB与O相离，故选：C．【点拨】本题考查了直线与圆的位置，解题的关键是掌握直线与圆的位置关系．例4．已知O的半径为3，圆心O到直线AB的距离为5，则直线AB与O的位置关系（）A．相交B．相切C．相离D．相交或相切【答案】C【分析】根据O的半径为3，圆心O到直线AB的距离为5得3r，5d，可得rd，即可得．【详解】解：∵O的半径为3，圆心O到直线AB的距离为5，∴3r，5d，∴rd，∴直线AB与O相离，故选：C．【点拨】本题考查了直线与圆的位置，解题的关键是掌握直线与圆的位置关系．例5．如图，ABC内接于O，过A点作直线DE，当BAE（）时，直线DE与O相切．A．BB．BACC．CD．DAC【答案】C【分析】首先过点O作直径AF，连接BF，根据同弧所对的圆周角相等可得∠C＝∠AFB，进而可得到∠BAE＝∠F，再根据直径所对的圆周角是90°，可证出∠AFB+∠BAF＝90°，再利用等量代换可得∠BAE+∠BAF＝90°，进而得到直线DE与⊙O相切．【详解】解：当BAEC时，直线DE与O相切．理由如下：作AF交圆O于F点，连接BF．∵∠F，∠C是同弧AB所对的角，∴∠C＝∠F，∵∠BAE＝∠C，∴∠BAE＝∠F，∵AF为直径，∴∠ABF＝90°，∴在三角形ABF中，∠F+∠BAF＝90°，∵∠F＝∠BAE，∴∠BAE+∠BAF＝90°，∴FA⊥DE，∴直线DE与⊙O相切．故选：C．例5．如图，ABC内接于O，过A点作直线DE，当BAE（）时，直线DE与O相切．A．BB．BACC．CD．DAC【答案】C【分析】首先过点O作直径AF，连接BF，根据同弧所对的圆周角相等可得∠C＝∠AFB，进而可得到∠BAE＝∠F，再根据直径所对的圆周角是90°，可证出∠AFB+∠BAF＝90°，再利用等量代换可得∠BAE+∠BAF＝90°，进而得到直线DE与⊙O相切．【详解】解：当BAEC时，直线DE与O相切．理由如下：作AF交圆O于F点，连接BF．∵∠F，∠C是同弧AB所对的角，∴∠C＝∠F，∵∠BAE＝∠C，∴∠BAE＝∠F，∵AF为直径，∴∠ABF＝90°，∴在三角形ABF中，∠F+∠BAF＝90°，∵∠F＝∠BAE，∴∠BAE+∠BAF＝90°，∴FA⊥DE，∴直线DE与⊙O相切．故选：C．例6．如图为ABC的内切圆，点D，E分别为边AB，AC上的点，且DE为I的切线，若ABC的周长为21，BC边的长为6，则ADEV的周长为（）A．15B．9C．7.5D．7【答案】B【详解】解：ABC的周长为21，6BC，21615ACAB，设I与ABC的三边AB、BC、AC的切点为M、N、Q，切DE为P，DMDP，BNBM，CNCQ，EQEP，6BMCQBNCNBC，ADEV的周长ADDEAEADAEDPPEADDMAEEQABBMACCQACABBMCQ1569，故选B．例6．如图为ABC的内切圆，点D，E分别为边AB，AC上的点，且DE为I的切线，若ABC的周长为21，BC边的长为6，则ADEV的周长为（）A．15B．9C．7.5D．7【答案】B【详解】解：ABC的周长为21，6BC，21615ACAB，设I与ABC的三边AB、BC、AC的切点为M、N、Q，切DE为P，DMDP，BNBM，CNCQ，EQEP，6BMCQBNCNBC，ADEV的周长ADDEAEADAEDPPEADDMAEEQABBMACCQACABBMCQ1569，故选B．强化训练1．在同圆中，下列命题正确的有（）①平行弦所夹的弧相等；②三角形两个角的角平分线与外接圆的交点间的劣弧度数与第三个角的度数互补；③一个点到圆上各点的连线中，最大值为a，最小值为b，则圆的直径为ab；④若一个点到圆上不同三点的距离相等，则这个点一定是圆心．A．4个B．3个C．2个D．1个1．在同圆中，下列命题正确的有（）①平行弦所夹的弧相等；②三角形两个角的角平分线与外接圆的交点间的劣弧度数与第三个角的度数互补；③一个点到圆上各点的连线中，最大值为a，最小值为b，则圆的直径为ab；④若一个点到圆上不同三点的距离相等，则这个点一定是圆心．A．4个B．3个C．2个D．1个【答案】B【详解】解：①平行弦所夹的弧相等，正确；②如图，O是ABC的外接圆，BE平分ABC，CF平分ACB，求证：FAE的度数+180A．证明：∵BE平分ABC，CF平分ACB，∴AF的度数12AB的度数，»AE的度数12AC的度数，∵AB的度数2ACB，AC的度数2ABC，∴AF的度数ACB，»AE的度数ABC，∵180ACBABCA，∴FAE的度数+180A．∴三角形两个角的角平分线与外接圆的交点间的劣弧度数与第三个角的度数互补正确；③假设,PAaPBb．如图2，当点在圆内时，圆的直径为ABPAPBab；如图3，当点在圆外时，圆的直径为ABPAPBab．∴一个点到圆上各点的连线中，最大值为a，最小值为b，则圆的直径为ab或ab，故不正确；④若一个点到圆上不同三点的距离相等，则这个点一定是圆心，正确．答案是B．【答案】B【详解】解：①平行弦所夹的弧相等，正确；②如图，O是ABC的外接圆，BE平分ABC，CF平分ACB，求证：FAE的度数+180A．证明：∵BE平分ABC，CF平分ACB，∴AF的度数12AB的度数，»AE的度数12AC的度数，∵AB的度数2ACB，AC的度数2ABC，∴AF的度数ACB，»AE的度数ABC，∵180ACBABCA，∴FAE的度数+180A．∴三角形两个角的角平分线与外接圆的交点间的劣弧度数与第三个角的度数互补正确；③假设,PAaPBb．如图2，当点在圆内时，圆的直径为ABPAPBab；如图3，当点在圆外时，圆的直径为ABPAPBab．∴一个点到圆上各点的连线中，最大值为a，最小值为b，则圆的直径为ab或ab，故不正确；④若一个点到圆上不同三点的距离相等，则这个点一定是圆心，正确．答案是B．2．如图，O为锐角三角形ABC的外心，四边形OCDE为正方形，其中E点在ABC的外部，判断下列叙述不正确的是（）A．O是AEB△的外心，O不是AED△的外心B．O是BEC的外心，O不是BCD△的外心C．O是AEC△的外心，O不是BCD△的外心D．O是ADB的外心，O不是ADC△的外心2．如图，O为锐角三角形ABC的外心，四边形OCDE为正方形，其中E点在ABC的外部，判断下列叙述不正确的是（）A．O是AEB△的外心，O不是AED△的外心B．O是BEC的外心，O不是BCD△的外心C．O是AEC△的外心，O不是BCD△的外心D．O是ADB的外心，O不是ADC△的外心【答案】C【分析】根据三角形的外心得出OAOCOA，根据正方形的性质得出OAOCOD，求出OAOBOCOEOD，再逐个判断即可．【详解】解：连接OB、OD、OA，O为锐角三角形ABC的外心，OAOCOA，四边形OCDE为正方形，OAOCOD，OAOBOCOEOD，即O不是AED△的外心，OAOEOB，即O是AEB△的外心，OAOCOE，即O是ACE△的外心，OBOAOD，即O不是ABD△的外心，故选：C．【点拨】本题考查了正方形的性质和三角形的外心与外接圆，能熟记知识点的内容是解此题的关键，注意：三角形的外心到三个顶点的距离相等，正方形的四边都相等．【答案】C【分析】根据三角形的外心得出OAOCOA，根据正方形的性质得出OAOCOD，求出OAOBOCOEOD，再逐个判断即可．【详解】解：连接OB、OD、OA，O为锐角三角形ABC的外心，OAOCOA，四边形OCDE为正方形，OAOCOD，OAOBOCOEOD，即O不是AED△的外心，OAOEOB，即O是AEB△的外心，OAOCOE，即O是ACE△的外心，OBOAOD，即O不是ABD△的外心，故选：C．【点拨】本题考查了正方形的性质和三角形的外心与外接圆，能熟记知识点的内容是解此题的关键，注意：三角形的外心到三个顶点的距离相等，正方形的四边都相等．3．下列说法正确的是（）A．平分弦的直径垂直于弦B．三个点确定一个圆C．相等的圆心角所对的弧相等D．圆内接四边形的对角互补【答案】D【分析】当被平分的这条弦是直径时，此时直径不一定垂直于被平分的弦，从而可判断A，过同一直线上的三个点不能作圆，从而可判断B，不在同圆或等圆中，相等的圆心角所对的弧不相等，从而可判断C，由圆的内接四边形的性质可判断D，从而可得答案.【详解】解：平分弦（不是直径）的直径垂直于弦，故A不符合题意；不在同一直线上三个点确定一个圆，故B不符合题意；在同圆或等圆中，相等的圆心角所对的弧相等，故C不符合题意；圆内接四边形的对角互补，正确，故D符合题意；故选D【点拨】本题考查的是圆的基本性质，垂径定理及其推论，圆心角，弧，弦之间的关系，确定圆的条件，圆的内接四边形的性质，掌握以上基础知识是解题的关键.3．下列说法正确的是（）A．平分弦的直径垂直于弦B．三个点确定一个圆C．相等的圆心角所对的弧相等D．圆内接四边形的对角互补【答案】D【分析】当被平分的这条弦是直径时，此时直径不一定垂直于被平分的弦，从而可判断A，过同一直线上的三个点不能作圆，从而可判断B，不在同圆或等圆中，相等的圆心角所对的弧不相等，从而可判断C，由圆的内接四边形的性质可判断D，从而可得答案.【详解】解：平分弦（不是直径）的直径垂直于弦，故A不符合题意；不在同一直线上三个点确定一个圆，故B不符合题意；在同圆或等圆中，相等的圆心角所对的弧相等，故C不符合题意；圆内接四边形的对角互补，正确，故D符合题意；故选D【点拨】本题考查的是圆的基本性质，垂径定理及其推论，圆心角，弧，弦之间的关系，确定圆的条件，圆的内接四边形的性质，掌握以上基础知识是解题的关键.4．如图，直线abrr，垂足为H，点P在直线b上，6cmPH，O为直线b上一动点，若以2cm为半径的O与直线a相切，则OP的长为________．4．如图，直线abrr，垂足为H，点P在直线b上，6cmPH，O为直线b上一动点，若以2cm为半径的O与直线a相切，则OP的长为________．【答案】4cm或8cm【分析】分点O在点H的左侧、点O在点H的右侧两种情况，根据切线的性质计算即可．【详解】解：∵直线abrr，O为直线b上一动点，∴O与直线a相切时，切点为H，∴2cmOH，当点O在点H的左侧，O与直线a相切时，如图1所示：624OPPHOH（cm）；当点O在点H的右侧，O与直线a相切时，如图2所示：628OPPHOH（cm）；∴O与直线a相切，OP的长为4cm或8cm，故答案为：4cm或8cm．【点拨】本题考查的是切线的性质，熟练掌握切线的性质、灵活运用分情况讨论思想是解题的关键．【答案】4cm或8cm【分析】分点O在点H的左侧、点O在点H的右侧两种情况，根据切线的性质计算即可．【详解】解：∵直线abrr，O为直线b上一动点，∴O与直线a相切时，切点为H，∴2cmOH，当点O在点H的左侧，O与直线a相切时，如图1所示：624OPPHOH（cm）；当点O在点H的右侧，O与直线a相切时，如图2所示：628OPPHOH（cm）；∴O与直线a相切，OP的长为4cm或8cm，故答案为：4cm或8cm．【点拨】本题考查的是切线的性质，熟练掌握切线的性质、灵活运用分情况讨论思想是解题的关键．5．如图，在平面直角坐标系xOy中，P为x轴正半轴上一点．已知点0,1A，0,7B，M为ABP的外接圆．（1）点M的纵坐标为________；（2）当APB最大时，点P的坐标为________．5．如图，在平面直角坐标系xOy中，P为x轴正半轴上一点．已知点0,1A，0,7B，M为ABP的外接圆．（1）点M的纵坐标为________；（2）当APB最大时，点P的坐标为________．【答案】470，【详解】解：（1）∵0,1A，0,7B，∴线段AB的垂直平分线为直线1742y，∵点M在AB的垂直平分线上，∴点M的纵坐标为4，（2）过点0,1A，0,7B，作M与x轴相切，则点P在切点处时，APB最大，理由：如上图，若点P是x轴正半轴上异于切点P的任意一点，设AP交M于点E，连接AE，则AEBAPB，∵AEB是APEV的外角，∴AEBAPB，∴APBAPB，即点P在切点处时，APB最大，∵M经过点0,1A，0,7B，∴点M在线段AB的垂直平分线上，即点M在直线4y上，∵M与x轴相切于点P，MPx轴，从而4MP，即M的半径为4，设AB的中点为D，连接MDAM、，如上图，则MDAB，132ADBDAB，4AMMP，∵90POD，MPx轴，MDAB，∴四边形OPMD是矩形，从而OPMD，由勾股定理，得2222374MDAMAD，∴7OPMD，∴点P的坐标为70，，故答案为：4，70，．【答案】470，【详解】解：（1）∵0,1A，0,7B，∴线段AB的垂直平分线为直线1742y，∵点M在AB的垂直平分线上，∴点M的纵坐标为4，（2）过点0,1A，0,7B，作M与x轴相切，则点P在切点处时，APB最大，理由：如上图，若点P是x轴正半轴上异于切点P的任意一点，设AP交M于点E，连接AE，则AEBAPB，∵AEB是APEV的外角，∴AEBAPB，∴APBAPB，即点P在切点处时，APB最大，∵M经过点0,1A，0,7B，∴点M在线段AB的垂直平分线上，即点M在直线4y上，∵M与x轴相切于点P，MPx轴，从而4MP，即M的半径为4，设AB的中点为D，连接MDAM、，如上图，则MDAB，132ADBDAB，4AMMP，∵90POD，MPx轴，MDAB，∴四边形OPMD是矩形，从而OPMD，由勾股定理，得2222374MDAMAD，∴7OPMD，∴点P的坐标为70，，故答案为：4，70，．6．如图，ABC与O交于D，E两点，AB是直径且长为12，∥ODBC．(1)证明：CDDE；(2)若4AD，求CE的长度．6．如图，ABC与O交于D，E两点，AB是直径且长为12，∥ODBC．(1)证明：CDDE；(2)若4AD，求CE的长度．【详解】（1）证明：∵四边形ABED内接于O，DECA，∵OAOD，∴AADO，∵∥ODBC，∴CADOCDEC，CDDE＝；（2）解：连接,OEAE，由（1）得CA，∴12ABBC，2AOEBBAOD，，2AOEAOD，AODDOE，ADDE，28ACAD，∵AB是直径，∴90AEB，设CEx，则12BEx，∵2222ACCEABBE，∴222281212xx，解得：83x，∴83CE．【详解】（1）证明：∵四边形ABED内接于O，DECA，∵OAOD，∴AADO，∵∥ODBC，∴CADOCDEC，CDDE＝；（2）解：连接,OEAE，由（1）得CA，∴12ABBC，2AOEBBAOD，，2AOEAOD，AODDOE，ADDE，28ACAD，∵AB是直径，∴90AEB，设CEx，则12BEx，∵2222ACCEABBE，∴222281212xx，解得：83x，∴83CE．7．如图，AB是O的直径，点C在AB的延长线上，AD平分CAE交O于点D，且AECD，垂足为点E．(1)求证：直线CE是O的切线；(2)若3BC，32CD，求半径OB与线段AE的长．7．如图，AB是O的直径，点C在AB的延长线上，AD平分CAE交O于点D，且AECD，垂足为点E．(1)求证：直线CE是O的切线；(2)若3BC，32CD，求半径OB与线段AE的长．【详解】（1）连接OD，∵AD平分CAE，OAOD，∴EADOADODA，∴EAOD，∵AECD，∴ODCE，∴直线CE是O的切线．（2）连接OD，根据ODCE，∴2223OBODCD，∴222332OBOB，解得32OB．∵EAOD，∴4.5364ODOCAEAC．∴43232AE．【点拨】本题考查了切线的证明，勾股定理，平行线分线段成比例定理，熟练掌握切线的证明，勾股定理，平行线分线段成比例定理是解题的关键．【详解】（1）连接OD，∵AD平分CAE，OAOD，∴EADOADODA，∴EAOD，∵AECD，∴ODCE，∴直线CE是O的切线．（2）连接OD，根据ODCE，∴2223OBODCD，∴222332OBOB，解得32OB．∵EAOD，∴4.5364ODOCAEAC．∴43232AE．【点拨】本题考查了切线的证明，勾股定理，平行线分线段成比例定理，熟练掌握切线的证明，勾股定理，平行线分线段成比例定理是解题的关键．8．已知在RtABC△中，90ABC，以AB为直径的O交于AC点D，过圆心O作AC的平行经OE，交BC于点E，连接DE并延长交AB的延长线于点F．(1)求证：DF是O的切线；(2)若4,6BFDF，求DE．8．已知在RtABC△中，90ABC，以AB为直径的O交于AC点D，过圆心O作AC的平行经OE，交BC于点E，连接DE并延长交AB的延长线于点F．(1)求证：DF是O的切线；(2)若4,6BFDF，求DE．【详解】（1）证明：连接ODBD，，∵AB是⊙O的直径，∴90ADBBDC，∵OEAC∥，OAOB，∴1BEOBCEOA，∴BECE，∴DEBECE，∴DBEBDE，∵OBOD，∴OBDODB，∴90ODEOBE，∵点D在⊙O上，∴DF是⊙O的切线；（2）连接ODBD，，∵AB是⊙O的直径，∴90ADBBDC，∵OEAC∥，OAOB，∴1BEOBCEOA，∴BECE，∴DEBECE，设DEBECEx===，则6EFDFEDx，在BEF△中，90EBF，∴222EFBEBF，即22264xx，解得53x，∴53DE．【点拨】本题考查了切线的判定，平行线分线段成比例，勾股定理，掌握以上知识是解题的关键．【详解】（1）证明：连接ODBD，，∵AB是⊙O的直径，∴90ADBBDC，∵OEAC∥，OAOB，∴1BEOBCEOA，∴BECE，∴DEBECE，∴DBEBDE，∵OBOD，∴OBDODB，∴90ODEOBE，∵点D在⊙O上，∴DF是⊙O的切线；（2）连接ODBD，，∵AB是⊙O的直径，∴90ADBBDC，∵OEAC∥，OAOB，∴1BEOBCEOA，∴BECE，∴DEBECE，设DEBECEx===，则6EFDFEDx，在BEF△中，90EBF，∴222EFBEBF，即22264xx，解得53x，∴53DE．【点拨】本题考查了切线的判定，平行线分线段成比例，勾股定理，掌握以上知识是解题的关键．9．如图，O是ABC的外接圆，AE切O于点A，AE与直径BD的延长线相交于点E．(1)如图①，若70C，求E的大小；(2)如图②，若AEAB，求E的大小．9．如图，O是ABC的外接圆，AE切O于点A，AE与直径BD的延长线相交于点E．(1)如图①，若70C，求E的大小；(2)如图②，若AEAB，求E的大小．【详解】（1）连接OA．如图①，AE切O于点A，OAAE，90OAE，70C，2270140AOBC，又180AOBAOE，40AOE，90AOEE，904050E．（2）连接OA，如图②，设Ex．ABAE，ABEEx，OAOB，OABABOx，2AOEABOBAOx．AE是O的切线，OAAE，即90OAE，在OAE中，90AOEE，即290xx，解得30x，30E．【点拨】本题主要考查了切线的性质，等腰三角形的性质，圆周角的性质，三角形内角和的性质，用方程思想解决几何问题，关键是熟悉掌握这些性质．【详解】（1）连接OA．如图①，AE切O于点A，OAAE，90OAE，70C，2270140AOBC，又180AOBAOE，40AOE，90AOEE，904050E．（2）连接OA，如图②，设Ex．ABAE，ABEEx，OAOB，OABABOx，2AOEABOBAOx．AE是O的切线，OAAE，即90OAE，在OAE中，90AOEE，即290xx，解得30x，30E．【点拨】本题主要考查了切线的性质，等腰三角形的性质，圆周角的性质，三角形内角和的性质，用方程思想解决几何问题，关键是熟悉掌握这些性质．10．如图，AB是O的直径，点C是O上的一点，ODAB交AC于点E，2DA．(1)求证：CD是O的切线；(2)求证：DEDC；(3)若10OD，6CD，求AE的长．10．如图，AB是O的直径，点C是O上的一点，ODAB交AC于点E，2DA．(1)求证：CD是O的切线；(2)求证：DEDC；(3)若10OD，6CD，求AE的长．【详解】（1）证明：连接OC，如图，OAOC，ACOA，2COBAACOA，又2DA，DCOB．又ODAB，90COBCOD，90DCOD，即90DCO，OCDC，又点C在O上，CD是O的切线；（2）证明：90DCO，90DCEACO，又ODAB，90AEOA，又AACO，DECAEO，DECDCE，DEDC；（3）解：90DCO，10OD，6DC，22221068OCODDC，8OAOC，又6DEDC，4OEODDE，在RtAEO中，由勾股定理得：222228480AEOAOE，45AE．【详解】（1）证明：连接OC，如图，OAOC，ACOA，2COBAACOA，又2DA，DCOB．又ODAB，90COBCOD，90DCOD，即90DCO，OCDC，又点C在O上，CD是O的切线；（2）证明：90DCO，90DCEACO，又ODAB，90AEOA，又AACO，DECAEO，DECDCE，DEDC；（3）解：90DCO，10OD，6DC，22221068OCODDC，8OAOC，又6DEDC，4OEODDE，在RtAEO中，由勾股定理得：222228480AEOAOE，45AE．谢谢观看！