《立体几何中的向量方法》人教版高中数学选修2-1PPT课件（第3课时）.pptx

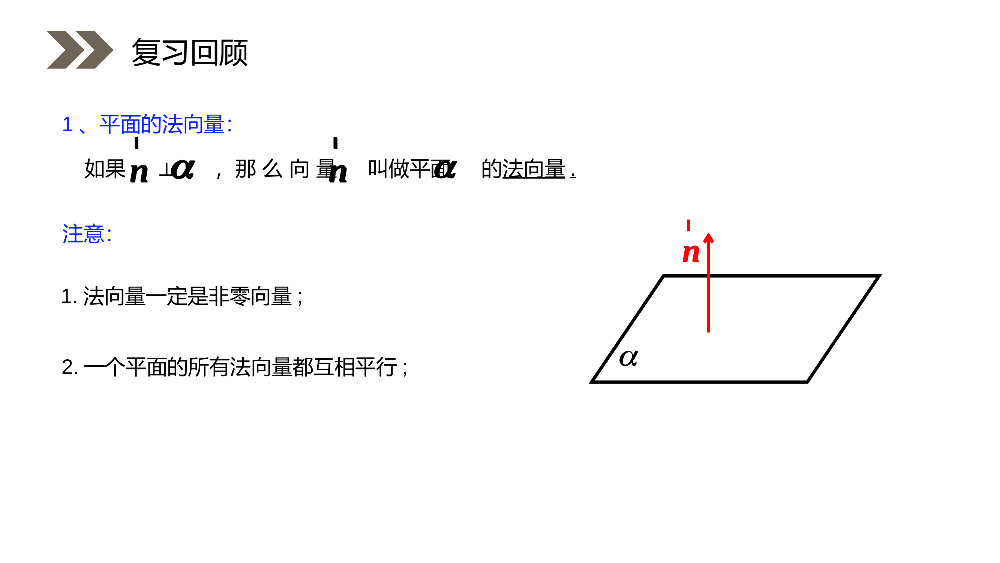
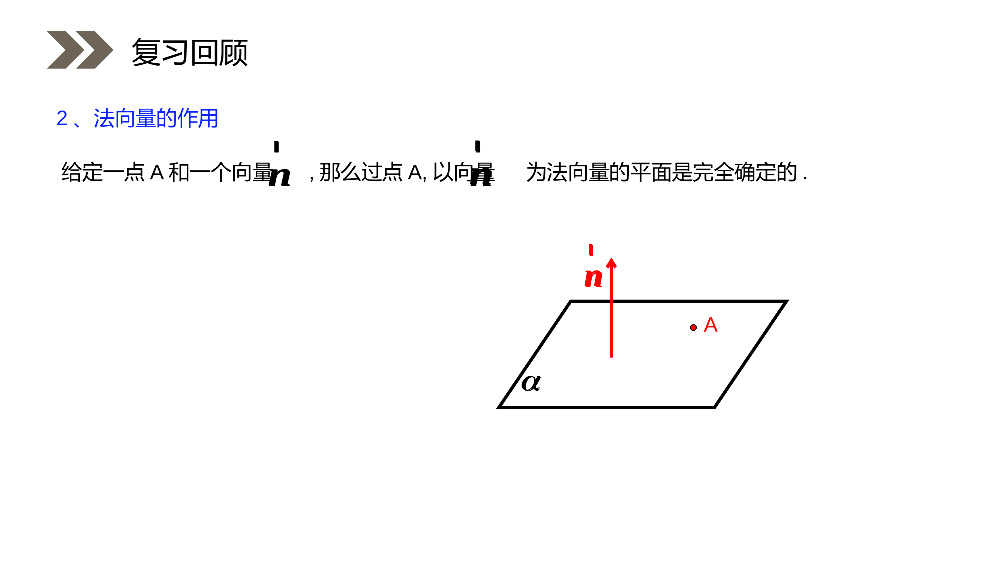
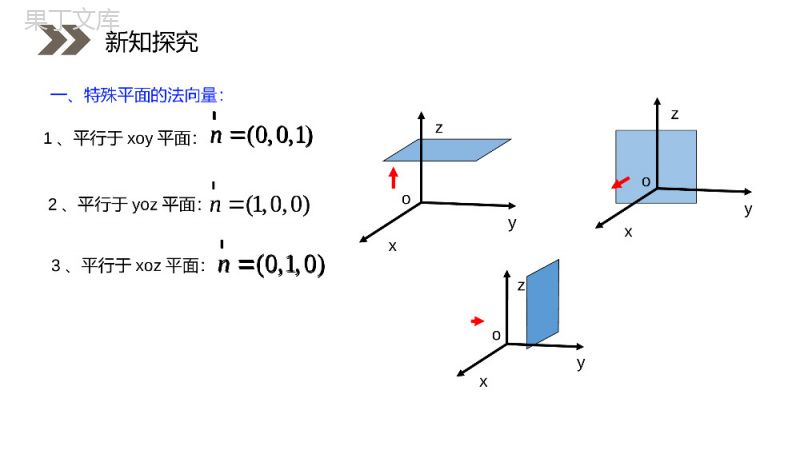
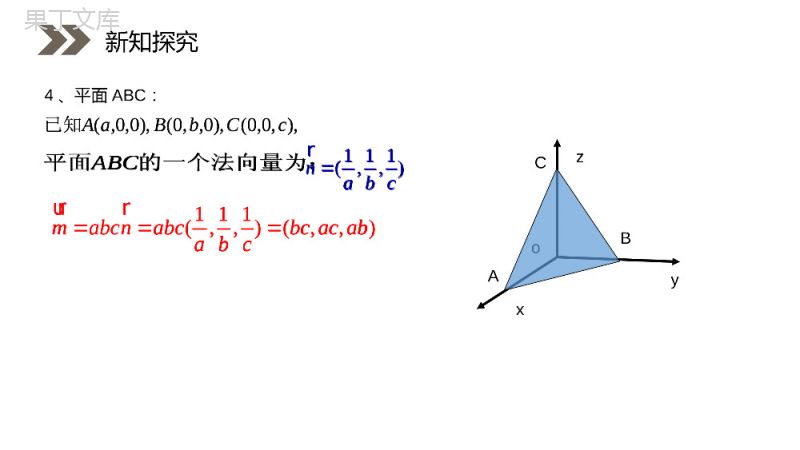
人教版高中数学选修2-1讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-13.2立体几何中的向量方法第三课时第3章空间向量与立体几何如果⊥，那么向量叫做平面的法向量.nrnrnr1、平面的法向量：2.一个平面的所有法向量都互相平行;注意：1.法向量一定是非零向量;复习回顾nrnrnrnr给定一点A和一个向量,那么过点A,以向量为法向量的平面是完全确定的.nrnrA2、法向量的作用复习回顾nrnrnr一、特殊平面的法向量：1、平行于xoy平面：yzxoyzxoyzxo(0,0,1)nr(1,0,0)nr(0,1,0)nr3、平行于xoz平面：2、平行于yoz平面：新知探究(0,0,1)nr(1,0,0)nr(0,1,0)nr的一个法向量为：平面ABC111(,,)nabcr),,0,0(),0,,0(),0,0,(cCbBaA已知yzxoABC4、平面ABC：111(,,)(,,)mabcnabcbcacababcurr新知探究的一个法向量为：平面ABC111(,,)nabcr),,0,0(),0,,0(),0,0,(cCbBaA已知111(,,)(,,)mabcnabcbcacababcurr.7zyzx解得：.)1,1,7(,1mz令二、一般平面的法向量：例1、已知平面的两个向量为，，求此平面的一个法向量.)9,5,2(b)4,3,1(a解：设为平面的法向量，则有),,(zyxm,00mbma,0952043zyxzyx即新知探究.7zyzx解得：.)1,1,7(,1mz令)9,5,2(b)4,3,1(a),,(zyxm,00mbma,0952043zyxzyx即第一步(设):设出平面法向量的坐标为(,,);nxyzr11122200axbyczaxbycz第三步(列):根据且可列出方程组0nbrr0narr第四步(解):把看作常数,用表示、.xyzz第五步(取):取为任意一个正数(取得越特殊越好),便得到平面法向量的坐标.znr第二步(找):找出（求出）平面内的两个不共线的111(,,),aabcr向量坐标为222(,,)babcr方法总结(,,);nxyzr11122200axbyczaxbycz0nbrr0narrxyzzznr111(,,),aabcr222(,,)babcr解:设平面ABC的一个法向量为(,,)nxyz则nABnAC，.∵(3,4,0)AB,(3,0,2)AC∴(,,)(3,4,0)0(,,)(3,0,2)0xyzxyz即340320xyxz∴3432yxzx取4x,则(4,3,6)n∴(4,3,6)n是平面ABC的一个法向量.巩固训练练习1：在空间直角坐标系中,已知,,试求平面ABC的一个法向量.解:设平面ABC的一个法向量为(,,)nxyz则nABnAC，.∵(3,4,0)AB,(3,0,2)AC∴(,,)(3,4,0)0(,,)(3,0,2)0xyzxyz即340320xyxz∴3432yxzx取4x,则(4,3,6)n∴(4,3,6)n是平面ABC的一个法向量.解:设平面ABC的一个法向量为(,,)nxyz则nABnAC，.∴(,,)(2,2,1)0(,,)(4,5,3)0xyzxyz即2204530xyzxyz∴22yxzx①∵2221xyz②∴由①②得13x∴平面ABC的单位法向量为122(333，，）或122(333，，）.巩固训练练习2：已知求平面的单位法向量.解:设平面ABC的一个法向量为(,,)nxyz则nABnAC，.∴(,,)(2,2,1)0(,,)(4,5,3)0xyzxyz即2204530xyzxyz∴22yxzx①∵2221xyz②∴由①②得13x∴平面ABC的单位法向量为122(333，，）或122(333，，）.DABCGFExyz由题设C(0,0,0)，A(4,4,0)，B(0,4,0)，D(4,0,0)，E(2,4,0)，F(4,2,0)，G(0,0,2)．(2,2,0),(2,4,2),EFEGuuuruuur设平面EFG的一个法向量为(,,)nxyznEFnEG，ruuurruuurQ2202420xyxyZ(1,1,3),n3,=1=1zxy令得，，解：如图，建立空间直角坐标系C－xyz．练习3:如图，已知正方形ABCD的边长为4，E、F分别是AB、AD的中点，GC⊥平面ABCD，且GC＝2，建立适当的空间直角坐标系，求平面EFG的一个法向量.巩固训练由题设C(0,0,0)，A(4,4,0)，B(0,4,0)，D(4,0,0)，E(2,4,0)，F(4,2,0)，G(0,0,2)．(2,2,0),(2,4,2),EFEGuuuruuur设平面EFG的一个法向量为(,,)nxyznEFnEG，ruuurruuurQ2202420xyxyZ(1,1,3),n3,=1=1zxy令得，，1:（2010浙江理数）如图,在矩形ABCD中,点E,F分别在线段AB,AD上，沿直线EF将翻成,使平面.（Ⅰ）求二面角A’-FD-C的余弦值；243AEEBAFFDAEFEFA''AEFBEF平面应用训练AEFEFA')0,8,10(),0,0,10(),0,0,4(),0,0,0(432,,:CDFAFDAFEBAEyxABADA轴，建系如图：所在直线分别为为坐标原点，以以解)0,8,0(),0,0,6(),22,2,2('),22,2,2(',',',''DCFDFAAABCDHAEFAEFEFAEFHAAFAEHAHEF面于面面又，，连接中点取，令的法向量，则为面设100nzFDnFAnFDAzyx''),,(),12,(0n),,(120n的法向量，为面FDCm),,(100.cos,,,cos3333则设二面角的大小为则nmnmnm应用训练)0,8,10(),0,0,10(),0,0,4(),0,0,0(432,,:CDFAFDAFEBAEyxABADA轴，建系如图：所在直线分别为为坐标原点，以以解)0,8,0(),0,0,6(),22,2,2('),22,2,2(',',',''DCFDFAAABCDHAEFAEFEFAEFHAAFAEHAHEF面于面面又，，连接中点取，令的法向量，则为面设100nzFDnFAnFDAzyx''),,(),12,(0n),,(120n的法向量，为面FDCm),,(100.cos,,,cos3333则设二面角的大小为则nmnmnm例2如图所示，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB＝2，AF＝1，M是线段EF的中点．求证：(1)AM∥平面BDE；(2)AM⊥平面BDF.应用训练证明：(1)建立如图所示的空间直角坐标系，设AC∩BD＝N，连接NE.则点N、E的坐标分别为(22，22，0)、(0,0,1)．∴NE＝(－22，－22，1)．又点A、M的坐标分别是(2，2，0)、(22，22，1)，∴AM＝(－22，－22，1)．∴NE＝AM且NE与AM不共线．∴NE∥AM.又∵NE平面BDE，AM平面BDE.∴AM∥平面BDE.应用训练感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明(2)由(1)知AM＝(－22，－22，1)，∵D(2，0,0)，F(2，2，1)，∴DF＝(0，2，1)．∴AM·DF＝0.∴AM⊥DF.同理AM⊥BF.又DF∩BF＝F，∴AM⊥平面BDF.应用训练人教版高中数学选修2-1讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-1感谢你的聆听第3章空间向量与立体几何