《函数的极值与导数》人教版高中数学选修2-2PPT课件（第1.3.2课时）.pptx

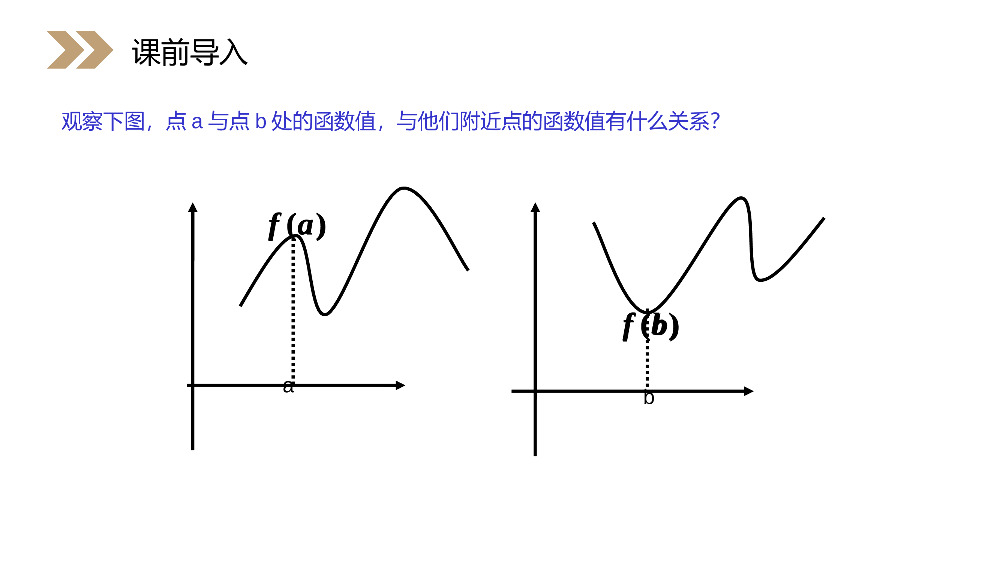
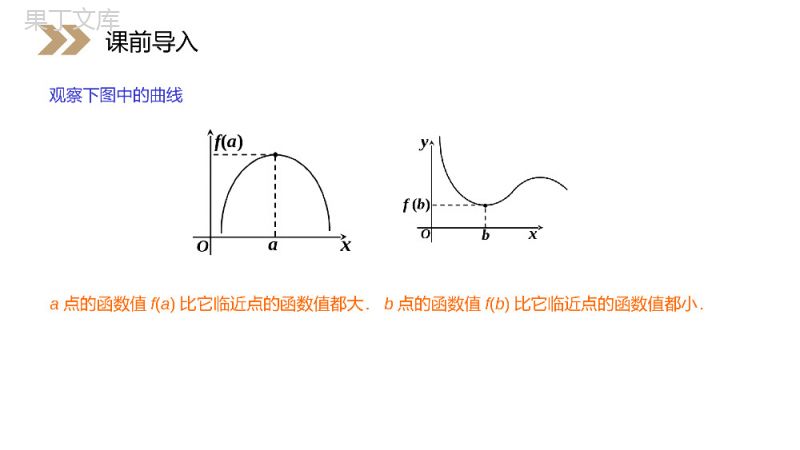
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-21.3.2函数的极值与导数第1章导数及其应用人教版高中数学选修2-2''在某个区间a,b内,如果fx>0,那么函数y=fx在这个区间内单调递增;如果fx<0,那么函数y=fx在这个区间内单调递减.一般地，函数的单调性与导数的关系：课前导入''在某个区间a,b内,如果fx>0,那么函数y=fx在这个区间内单调递增;如果fx<0,那么函数y=fx在这个区间内单调递减.（1）确定函数y=f(x)的定义域；（2）求导数f’(x)；（3）解不等式f’(x)>0，解集在定义域内的部分为增区间；（4）解不等式f’(x)<0，解集在定义域内的部分为减区间．课前导入求解函数单调区间的步骤观察下图，点a与点b处的函数值，与他们附近点的函数值有什么关系？ab)(bf)(af课前导入)(bf)(af观察下图中的曲线a点的函数值f(a)比它临近点的函数值都大．b点的函数值f(b)比它临近点的函数值都小．课前导入观察函数f(x)＝2x3－6x2＋7的图象思考：函数y＝f(x)在点x＝0，x＝2处的函数值，与它们附近所有各点处的函数值，比较有什么特点?课前导入htom()hftM新知探究观察()hftMthOa83.1图0th'单调递增0th'单调递减0ah'93.1图观察上图，可以发现t=a时，高台跳水运动员距水面的高度最大，那么函数在此点的导数是多少？此点附近的图像有什么特点？相应的，导数的符号有什么变化规律？新知探究thOa83.1图0th'单调递增0th'单调递减0ah'93.1图0th'单调递增0th'单调递减0ah'93.1图放大t=a附近函数h(t)的图像，如图所示，可以看出'0ha'0.ht当t>a时，函数h(t)单调递减，'0;ht当tf(x0)我们就说f(x0)是函数f(x)的一个极小值，记作y极小值=f(x0).极大值和极小值统称极值极小值的概念思考：极值与我们前面学过的最值的概念有什么区别？极值反映了函数在某一点附近的大小情况，刻画的势函数的局部性质.新知探究3144.3fxxx求函数的极值3'2144,4322.fxxxfxxxx解:因为所以下面分两种情况讨论：例题讲解3144.3fxxx求函数的极值3'2144,4322.fxxxfxxxx解:因为所以;2x,2x,0xf1'时或即当.2x2,0xf2'时即当:xf,xf,x'的变化情况如下表变化时当单调递增单调递减单调递增34328xf00xf,222,222,x'例题讲解;2x,2x,0xf1'时或即当.2x2,0xf2'时即当:xf,xf,x'的变化情况如下表变化时当单调递增单调递减单调递增34328xf00xf,222,222,x'因此,当x=-2时有极大值,y极大值=28/3;当x=2时有极小值,并且,y极小值=-4/3.31fx=x-4x+41.3-123函数的图象如图所示.22oxy4x4x31xf3123.1图例题讲解31fx=x-4x+41.3-123函数的图象如图所示.22oxy4x4x31xf3123.1图?极大值一定大于极小值吗导数值为0的点一定是函数的极值点吗?例题讲解你还能再举例吗？导数值为0的点不一定是函数的极值点.例如，函数，.虽然，但无论x>0，还是x<0，恒有，即函数是单调递增的，所以x=0不是函数极值点.3fx=x'2fx=3x'f0=0'fx>03fx=x3fx=x?极大值一定大于极小值吗导数值为0的点一定是函数的极值点吗?3fx=x'2fx=3x'f0=0'fx>03fx=x3fx=x一般地，函数y=f(x)在一点的导数值为0是函数y=f(x)在这点取极值的必要条件，而非充要条件.一般地，求函数y=f(x)的极值的方法是:解方程.当时：'0fx'00fx（1）如果在附近的左侧f′(x)>0，右侧f′(x)<0，那么是极大值；0x0fx口诀：左负右正为极小，左正右负为极大.'0'020,0,.xfxfxfx如果在附近的左侧右那么是极小值侧例题讲解'0fx'00fx0x0fx'0'020,0,.xfxfxfx如果在附近的左侧右那么是极小值侧求函数y＝(x2－1)3＋1的极值．解：定义域为R，y’＝6x(x2－1)2.由y’＝0可得x1＝－1，x2＝0，x3＝1当x变化时，y’，y的变化情况如下表：例题讲解当x＝0时，y有极小值，并且y极小值＝0．1.下列函数中，x=0是极值点的函数是（)A.y=-x3B.y=cos2xC.y=tanx-xD.y=1/xB课堂练习2.曲线y=x4-2x3+3x在点P(-1，0)处的切线的斜率为()A.–5B.–6C.–7D.–8B课堂练习3.下列说法正确的是（）A.函数在闭区间上的极大值一定比极小值大B.函数在闭区间上的最大值一定是极大值C.对于f(x)=x3+px2+2x+1，若p<√6，则f(x)无极值D.函数f(x)在区间(a,b)上一定存在最值C课堂练习5.函数y=x3-3x的极大值为_____.26.对可导函数，在一点两侧的导数异号是这点为极值点___________.充要条件4.已知y=f(x)=2x3-3x2+a的极大值为6，那么a等于()A.6B.0C.5D.1A课堂练习7.求函数的极值.)0()(2axaxxf解:函数的定义域为(,0)(0,),222()()()1.axaxafxxx令,解得x1=-a，x2=a(a>0).()0fx当x变化时,，f(x)的变化情况如下表:()fx课堂练习)0()(2axaxxf(,0)(0,),222()()()1.axaxafxxx()0fx()fxx(-∞,-a)-a(-a,0)(0,a)a(a,+∞)f’(x)+0--0+f(x)↗极大值-2a↘↘极小值2a↗故当x=-a时,f(x)有极大值f(-a)=-2a;当x=a时,f(x)有极小值f(a)=2a.课堂练习（1）可导函数极值点的导数一定为0，但导数为0的点不一定都是极值点.（2）对于一般函数，函数的不可导点也可能是极值点.课堂小结（3）极大值与极小值的概念.（4）一般地，函数y=f(x)在一点的导数值为0是函数y=f(x)在这点取极值的必要条件，而非充分条件.（5）如果函数f(x)在点x0处连续,总结判别f(x0)是极大或极小值的方法：左负右正为极小，左正右负为极大.感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-2感谢你的聆听第1章导数及其应用人教版高中数学选修2-2