《定积分在几何中的应用》人教版高中数学选修2-2PPT课件（第1.7.1课时）.pptx

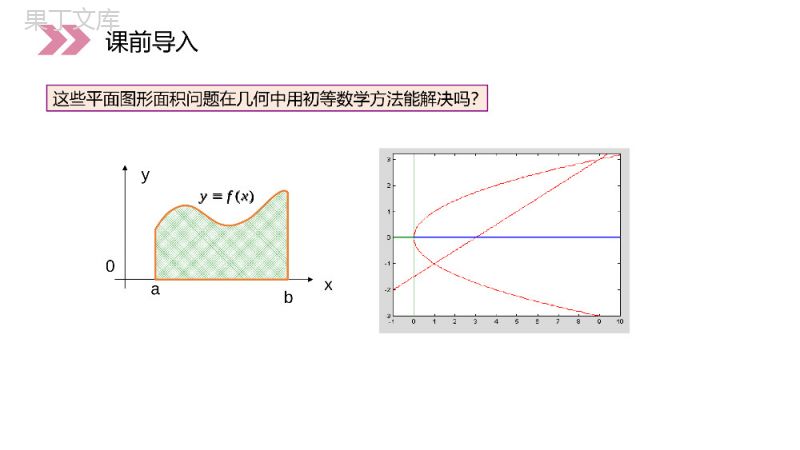
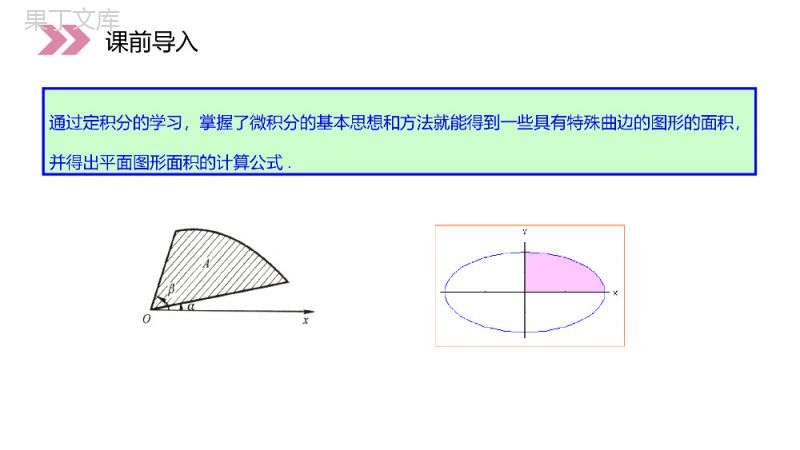
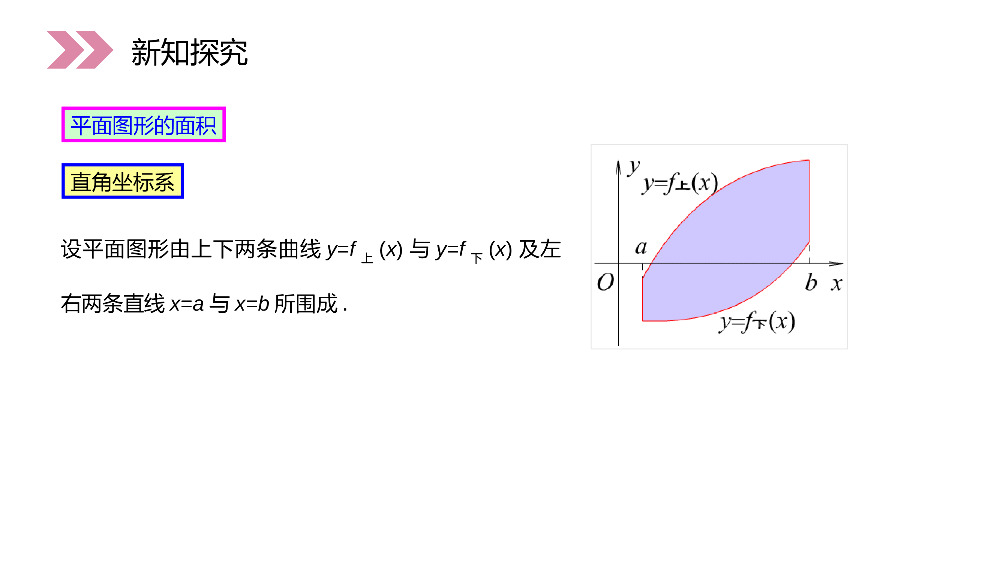
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-21.7.1定积分在几何中的应用第1章导数及其应用人教版高中数学选修2-2这些平面图形面积问题在几何中用初等数学方法能解决吗？)(xfya0xyb课前导入)(xfy通过定积分的学习，掌握了微积分的基本思想和方法就能得到一些具有特殊曲边的图形的面积，并得出平面图形面积的计算公式.课前导入第三步：写出整体量的近似值，niiii=1F=ΔFf(ξ)Δx(i=1,2,L,n);≈第四步：取时的则得λ=maxΔx0→niii=1fξΔxnbiiaλ0i=1F=limfξΔx=fxdx→第一步：将所求量分为部分量之和，即:;第二步：求出每个部分量的近似值，nii=1F=ΔFiiiΔF=f(ξ)Δxi=1,2,,n,用定积分概念解决实际问题的四个步骤：课前导入niiii=1F=ΔFf(ξ)Δx(i=1,2,L,n);≈λ=maxΔx0→niii=1fξΔxnbiiaλ0i=1F=limfξΔx=fxdx→nii=1F=ΔFiiiΔF=f(ξ)Δxi=1,2,,n,设平面图形由上下两条曲线y=f上(x)与y=f下(x)及左右两条直线x=a与x=b所围成.直角坐标系平面图形的面积新知探究[f上(x)-f下(x)]dx,它也就是面积元素.因此平面图形的面积为在点x处面积增量的近似值为dxxfxfSba)]()([下上新知探究由左右两条曲线x=j左(y)与x=j右(y)及上下两条直线y=d与y=c所围成的平面图形的面积如何表示为定积分？讨论：新知探究面积为面积元素为[j右(y)-j左(y)]dy,dcdyyyS)]()([左右提示：新知探究首先根据题意画出曲线的草图，在图中找出所求面积的区域，图形结合，直观解题；其次，为了确定出被积函数和积分的上、下限，我们需要求出两条曲线的交点的横坐标.22y=x,y=x计算两条抛物线在第一象限所围图形的面积.22y=x,y=x例1新知探究22y=x,y=x22y=x,y=x从图中可以看出，所求图形的面积可以为两个曲边梯形面积的差，进而可用定积分求面积S.xx+dx新知探究xx+dx解:方程组：2y=x2y=x得交点的横坐标(0,0),(1,1)因此，所求图形的面积为OABCOABD112003131200S=S-S=xdx-xdx21=x-x33211=-=333曲梯形曲梯形xx+dx新知探究2y=x2y=x(0,0),(1,1)OABCOABD112003131200S=S-S=xdx-xdx21=x-x33211=-=333曲梯形曲梯形xx+dx计算抛物线y2=、直线y=x-4和x轴所围成的图形的面积S.2x首先画出草图，并设法把所求图形的面积问题转化为求曲边梯形的面积问题.其次，确定被积函数和积分的上、下限.例2新知探究2xy=2x1S2S由图可知，我们需要把所求图形的面积分成两部分.需要求出直线y=x-4与曲线的交点的横坐标，直线y=x-4与x轴的交点.12SS和y=2x新知探究y=2x1S2S12SS和y=2xy=2x1S2S得直线y=x-4与曲线y=交点的坐标为(8,4).直线y=x-4与x轴的交点为(4,0).2x解：所求面积为图中阴影部分的面积.解方程组y=2x,y=x-4新知探究y=2x1S2S2xy=2x,y=x-4因此，所求图形面积为1248804433248822044S=S+S=2xdx+2xdx-x-4dx22221=x+x-x-433240=3新知探究1248804433248822044S=S+S=2xdx+2xdx-x-4dx22221=x+x-x-433240=3计算由曲线和所围成的图形的面积.3y=x6x2y=x首先画出草图，并设法把所求图形的面积问题转化为求两部分的面积问题.其次，确定被积函数和积分的上、下限.例3新知探究3y=x6x2y=x2xyxxy631S2S由图可知，我们需要把所求图形的面积分成两部分.需要求出曲线、曲线两个交点.12SS和2y=x3y=x-6x新知探究得两曲线的交点的坐标为(0,0),(-2,4),(3,9).解：所求面积为图中阴影部分的面积.解方程组23y=x,y=x-6x2xyxxy631S2S12SS和2y=x3y=x-6x23y=x,y=x-6x选x为积分变量x[-2,3]∈(1)x[-2,0],321dA=(x-6x-x)dx(2)x[0,3],232dA=(x-x+6x)dx于是所求面积21AAA033223-20A=(x-6x-x)dx+(x-x+6x)dx253=.12新知探究(1)x[-2,0],321dA=(x-6x-x)dx(2)x[0,3],232dA=(x-x+6x)dx21AAA033223-20A=(x-6x-x)dx+(x-x+6x)dx253=.12平面图形的面积求法小结：（1）画图（2）确定图形范围，通过解方程组确定上下限（3）确定被积函数（注意上下位置）（4）写出平面图形面积的积分表达式（5）利用微积分基本定理求出面积新知探究求由相交围成的平面图形的面积12y=f(x),y=g(x)若函数相交,则两条曲线所围形的面积为显然在具体的题目中,需要首先把函数的图形画出来,然后才写出具体的面积表达式.12y=f(x),y=g(x)bbaaS=g(x)dx-f(x)dx新知探究12y=f(x),y=g(x)12y=f(x),y=g(x)bbaaS=g(x)dx-f(x)dx曲边扇形面积元素21dA=[φ(θ)]dθ2曲边扇形的面积公式β2α1A=[j(θ)]dθ.2极坐标方程的情形xodd)(r设由曲线及射线围成一曲边扇形，求其面积.这里在上连续，且.r=φθθ=αθ=β、αβ，φθφθ0≥新知探究21dA=[φ(θ)]dθ2β2α1A=[j(θ)]dθ.2xodd)(rr=φθθ=αθ=β、αβ，φθφθ0≥因为曲线关于x轴对称，所以只须考虑第一象限中的情况.求曲线围成的图形的面积.2(2cos)(0)aa例4新知探究2(2cos)(0)aa取为积分变量,则设区间，所对应的曲边扇形的面积为则面积元素就是用区间所对应的扇形面积代替曲边扇形的面积.θ[0,π].θ[0,π],θ[θ,θ+dθ][θ,θ+dθ],A1dA新知探究θ[0,π].θ[0,π],θ[θ,θ+dθ][θ,θ+dθ],A1dA解：(1)确定积分变量和积分区间:取为积分变量，(2)求微元：任取则面积元素就是区间所对应的扇形面积,(3)求定积分：第一象限图形的面积表示为θ[0,π]θ[0,π],[θ,θ+dθ][0,π],1dA[θ,θ+dθ]211dA=ρdθ.2ππ2221001A=ρdθ=2a(2+cosθ)dθ2π2220=a(4+4cosθ+cosθ)dθ=9πa则所求的几何面积为21A=2A=18πa新知探究θ[0,π]θ[0,π],[θ,θ+dθ][0,π],1dA[θ,θ+dθ]211dA=ρdθ.2ππ2221001A=ρdθ=2a(2+cosθ)dθ2π2220=a(4+4cosθ+cosθ)dθ=9πa21A=2A=18πa设函数，若，则的值为__________.2fx=ax+ca0≠1000fxdx=fx,0x1≤≤0x1、课堂练习11200310200fxdx=ax+cdx1a=ax+cx=+c333=ax+cx=3∴2fx=ax+ca0≠1000fxdx=fx,0x1≤≤0x11200310200fxdx=ax+cdx1a=ax+cx=+c333=ax+cx=3∴求由所围成图形的面积.2x-y=0,y=x-2x2、课堂练习解：(1)确定积分变量和积分区间：由于曲线和的交点为和.取x为积分变量,则)0,0()3,3([0,3].xxxy220yx所求的几何图形的面积表示为320(3)Axxdx3209(3).2Axxdx2x-y=0,y=x-2x)0,0()3,3([0,3].xxxy220yx320(3)Axxdx3209(3).2Axxdx感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明直角坐标方程给出的平面图形的面积一般以直角坐标为积分变量；极坐标方程给出的平面图形的面积一般以由极坐标为积分变量；曲边梯形的面积的计算一般以由直角坐标为积分变量；曲边扇形的面积的计算一般以由极坐标为积分变量.课堂小结讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-2感谢你的聆听第1章导数及其应用人教版高中数学选修2-2