材料力学弯曲刚度,材料力学弯曲刚度计算公式

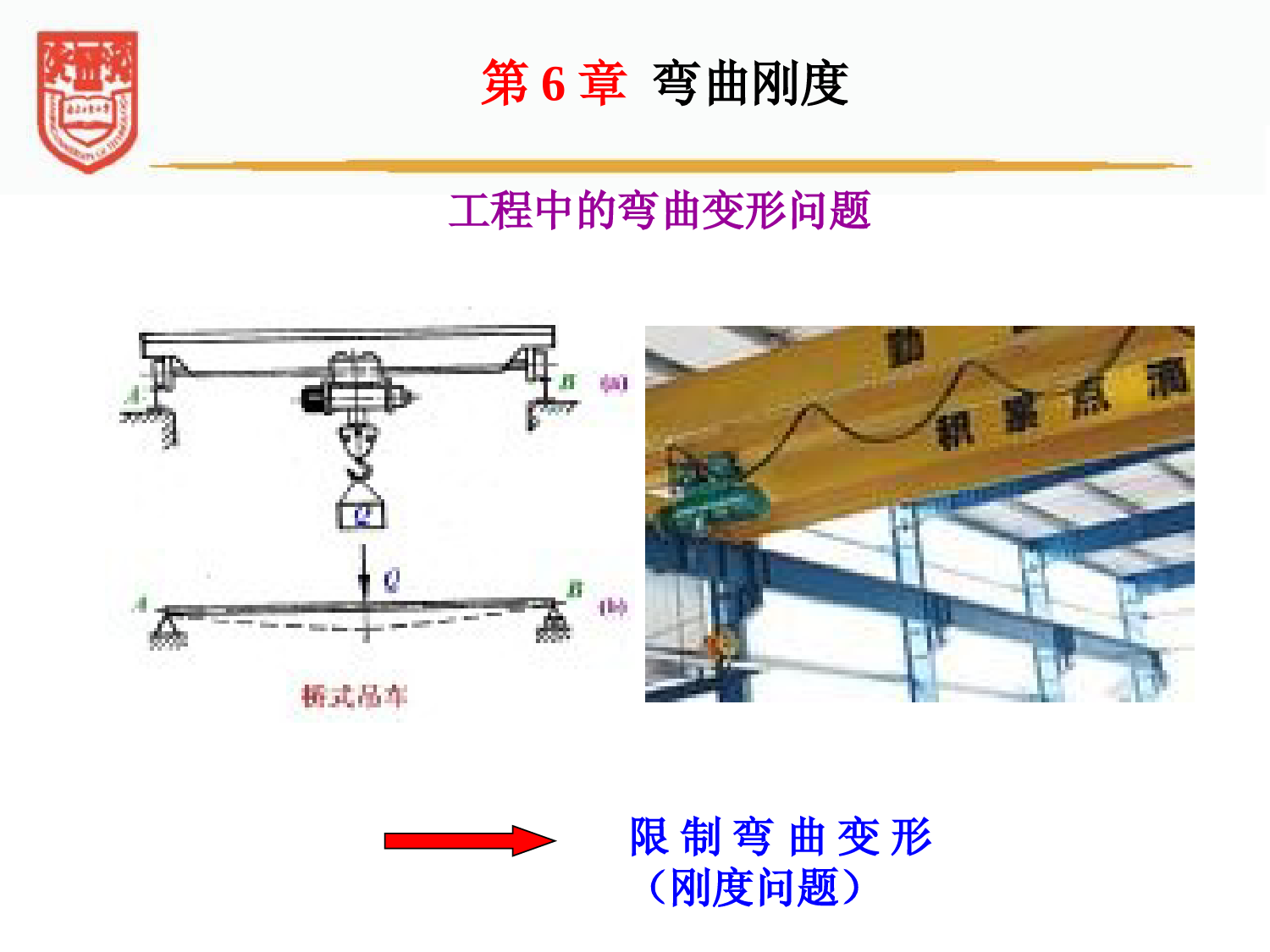
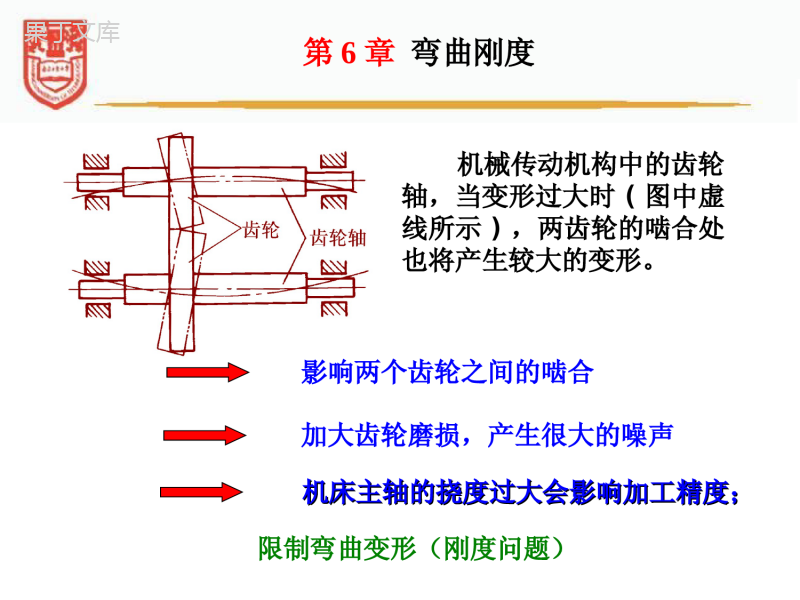
NanjingUniversityofTechnology材料力学(6)材料力学第6章弯曲刚度限制弯曲变形（刚度问题）工程中的弯曲变形问题第6章弯曲刚度机械传动机构中的齿轮轴，当变形过大时(图中虚线所示)，两齿轮的啮合处也将产生较大的变形。加大齿轮磨损，产生很大的噪声限制弯曲变形（刚度问题）影响两个齿轮之间的啮合机床主轴的挠度过大会影响加工精度；机床主轴的挠度过大会影响加工精度；第6章弯曲刚度各种车辆中用于减振的板簧，都是采用厚度不大的板条叠合而成。可以承受很大的力而不发生破坏能承受较大的弹性变形，吸收车辆受到振动和冲击时产生的动能，收到抗振和抗冲击的效果。利用弯曲变形（刚度问题）第6章弯曲刚度求解静不定问题第6章弯曲刚度ABF1/2L1/2L(+)(+)FL321FL5129FL5129静不定梁静不定梁建立补充方程利用弯曲变形（求解静不定问题）6.1梁的变形与位移6.3叠加法确定梁的挠度与转角6.5提高梁刚度的措施6.4梁的刚度问题6.2梁的小挠度微分方程及其积分第6章弯曲刚度6.6简单的静不定梁6.1梁的变形与位移第6章弯曲刚度BxwA■■取梁的左端点为坐标原点，梁变形前的轴线为x轴（向右为正），横截面的铅垂对称轴为w轴（向下为正），xw平面为纵向对称面。■■度量梁变形后横截面位置改变，即位移，有三个基本量。6.1梁的变形与位移1.基本概念B'ABxw转角B'挠度wCC'挠度deflection（ww）：横截面形心C（即轴线上的点）的铅垂位移。转角slope（）：变形后的横截面相对于变形前位置绕中性轴转过的角度。6.1梁的变形与位移ABxw转角B'挠度wCC'轴向位移（u）：横截面形心沿水平方向的位移。在小变形情形下，上述位移中，轴向位移u与挠度w相比为高阶小量，故通常不予考虑。6.1梁的变形与位移xwwddtan■■挠曲线：梁变形后的轴线。)(xww挠曲线ABxw转角B'挠度wCC'注意：当变形保持在弹性范围内，挠曲线为连续光滑曲线。挠度方程：)(x转角方程：2.挠度与转角的关系6.1梁的变形与位移在小变形条件下，挠度曲线较为平坦。即很小，因而上式中tan。于是有挠曲线ABxw转角B'w挠度CC'xwwddtanxwwdd挠度与转角的相互关系6.1梁的变形与位移■■挠度和转角符号的规定挠度：向下为正，向上为负。转角：顺时针转为正，逆时针转为负。挠曲线ABxw转角B'w挠度CC'6.1梁的变形与位移6.2梁的小挠度微分方程及其积分第6章弯曲刚度力学中的曲率公式数学中的曲率公式EIM123222dd1dd1xwxwx1.小挠度微分方程6.2梁的小挠度微分方程及其积分纯弯曲时曲率与弯矩的关系为横力弯曲时,M和都是x的函数。细长梁可以略去剪力对梁的位移的影响,则EIxMx1A'A'中性层曲率中心O'O'变形后zdxyxd-yy小挠度情形下对于弹性曲线的小挠度微分方程，式中的正负号与w坐标的取向有关。EIxMxwxw23222dd1dd1dd22xwEIxMxw22dd本书规定的坐标系为：x轴水平向右为正,w轴竖直向下为正。6.2梁的小挠度微分方程及其积分MMoxwoxwMM因此,M与w的正负号正好相反，所以EIMxw22dd0dd,022xwM0dd,022xwMEIxMdxwd)(22（小挠度微分方程）6.2梁的小挠度微分方程及其积分近似原因：（1）略去了剪力的影响；（2）小挠度略去了w2项。对于等截面梁，弯曲刚度为常量时dddlMxwxCxEIEIxMdxwd)(222.小挠度微分方程的积分积分一次：（转角方程）积分二次：DCxdxdxEIxMw)(（挠度方程）式中C、D为积分常数，由梁的约束条件决定。6.2梁的小挠度微分方程及其积分①在固定端处：xwAB梁的边界条件②在固定铰支座和滚动铰支座处：xABlw0,0,0wwxAA;0,0Awx.0,Bwlx3.小挠度微分方程积分常数的确定——梁的约束条件（边界条件和连续性条件）6.2梁的小挠度微分方程及其积分PABC梁的连续性条件CCCCwwABlaCMCCww①在集中力作用处：②在中间铰处：6.2梁的小挠度微分方程及其积分写出下图的边界条件、连续性条件：0,0AwxCCax，CCwwax，0,Bwlx0,0AwxCCax，CCwwax，BDBlwlx,EAhFByAlFCabBEAhDAlFCabB练习由M的方向确定轴线的凹凸性。由约束性质及连续光滑性确定挠度曲线的大致形状及位置。4.梁的连续光滑挠曲线的绘制6.2梁的小挠度微分方程及其积分试根据连续光滑性质以及约束条件，画出梁的挠度曲线的大致形状。√√××思考题思考题11××××弯矩？约束？连续光滑？试根据连续光滑性质以及约束条件，画出梁的挠度曲线的大致形状。思考题思考题22××××××√√弯矩？约束？连续光滑？试根据连续光滑性质以及约束条件，画出梁的挠度曲线的大致形状。思考题思考题33××××××√√弯矩？约束？连续光滑？例题例题11求：求：梁的挠度与转角方程，以及最大挠度和最大转角。左端固定、右端自由的悬臂梁承受均布荷载。均布荷载集度为q，梁的弯曲刚度为EI、长度为l。q、EI、l均已知。6.2梁的小挠度微分方程及其积分5、积分法求解小挠度微分方程举例解：1．建立Oxw坐标系2．建立梁的弯矩方程OOxxww6.2梁的小挠度微分方程及其积分xM(x)FQ(x)21()02Mxqlxxl3．建立微分方程并积分将上述弯矩方程代入小挠度微分方程，得2"12EIwMqlxEIxMdxwd)(22例题1OOxxww积分后，得到31'6EIwEIqlxC4124EIwqlxCxD2"12EIwMqlx6.2梁的小挠度微分方程及其积分例题14．利用约束条件确定积分常数固定端处的约束条件为：31'6EIwEIqlxC4124EIwqlxCxD00xw，d00dwxx，=33,624qlCqlDOOxxww6.2梁的小挠度微分方程及其积分例题15．确定挠度与转角方程31'6EIwEIqlxC4124EIwqlxCxD33,624qlCqlD336qlxlEI434424qwlxlxlEI6.2梁的小挠度微分方程及其积分6．确定最大挠度与最大转角从挠度曲线可以看出，在悬臂梁自由端处，挠度和转角均为最大值。于是，将x=l，分别代入挠度方程与转角方程，得到：3max6BqlEI4max8BqlwwEI例题1例题例题22求：求：加力点B的挠度和支承A、C处的转角。简支梁受力如图所示。FP、EI、l均为已知。6.2梁的小挠度微分方程及其积分解：1．确定梁约束力首先，应用静力学方法求得梁在支承A、C二处的约束力分别如图中所示。AB段解：2.分段建立梁的弯矩方程BC段于是，AB和BC两段的弯矩方程分别为1P3044lMxFxx2PP3444llMxFxFxxl－－6.2梁的小挠度微分方程及其积分例题23．将弯矩表达式代入小挠度微分方程并分别积分211P2d30d44wlEIMxFxxx1P3044lMxFxx2PP3444llMxFxFxxl－－222PP2d3d444wllEIMxFxFxxlx＝－－＋－6.2梁的小挠度微分方程及其积分例题2积分后，得211P2d30d44wlEIMxFxxx12P183CxFEI113P181DxCxFEIw4．利用约束条件和连续性条件确定积分常数x＝0，w1＝0;x＝l，w2＝0x＝l/4，w1＝w2;x＝l/4，1=222P2P242183ClxFxFEI223P3P246181DxClxFxFEIw222PP2d3d444wllEIMxFxFxxlx＝－－＋－6.2梁的小挠度微分方程及其积分D1＝D2=02P211287lFCC＝例题25．确定转角方程和挠度方程以及指定横截面的挠度与转角将所得的积分常数代入后,得到梁的转角和挠度方程为：22P378128FxxlEIAB段BC段xlxEIFxw23P128781222P317824128FlxxxlEIxllxxEIFxw233P128746181算得加力点B处的挠度和支承处A和C的转角分别为EIlFwB3P25632P7128AFlEI2P5128BFlEI－6.2梁的小挠度微分方程及其积分例题2讨论：讨论：积分法步骤总结积分法步骤总结处理具体问题时的注意点EIxMdxwd)(22确定约束力分段建立挠度微分方程并积分利用约束条件确定积分常数确定挠度与转角方程以及指定截面的挠度与转角分段写出弯矩方程6.3叠加法确定梁的挠度与转角第6章弯曲刚度1.叠加法前提★在小变形，服从胡克定律的前提下挠度、转角与荷载均为一次线性关系6.3叠加法确定梁的挠度与转角实用的工具：挠度表（P157）为方便工程计算，已将各种支承条件下的静定梁，在各种典型荷载作用下的挠度和转角表达式一一列出，并形成手册。重要的方法：叠加法（superpositionmethod）应用叠加原理及常见静定梁在简单荷载作用下的挠度和转角，得到常见静定梁在复杂荷载作用下的挠度与转角。6.3叠加法确定梁的挠度与转角6.3叠加法确定梁的挠度与转角6.3叠加法确定梁的挠度与转角简支梁受力如图所示，q、l、EI均为已知。求求：：C截面的挠度wC；B截面的转角B。例题例题336.3叠加法确定梁的挠度与转角2.第一类叠加法——应用于多个荷载作用的情形321CCCCwwww解：解：1.将梁上的荷载变为三种简单的情形。123BBBB6.3叠加法确定梁的挠度与转角例题32.由挠度表查得三种情形下C截面的挠度和B截面的转角。EIqlwEIqlwEIqlwCCC4342411614813845,,,,,EIqlEIqlEIqlBBB333231311612416.3叠加法确定梁的挠度与转角例题33.应用叠加法，将简单荷载作用时的结果分别叠加。,EIqlwwiCiC43138411EIqliBiB33148116.3叠加法确定梁的挠度与转角例题3讨论：讨论：叠加法应用于多个荷载作用的情形的解题步骤叠加法应用于多个荷载作用的情形的解题步骤处理具体问题时的注意点●将所得结果叠加●将其分解为各种荷载单独作用的情形●由挠度表分别查得各种情形下的挠度和转角二梁的受力(包括荷载与约束力)是否相同？二梁的弯矩是否相同？二梁的变形是否相同？二梁的位移是否相同？思考题思考题44位移不仅与变形有关，而且与约束有关。BC段有没有变形？有没有位移？没有变形为什么会有位移？FPABC总体变形是微段变形累加的结果。有位移不一定有变形。思考题思考题55BC段梁均视为刚体。悬臂梁受力如图所示，q、l、EI均为已知。求求：：C截面的挠度wC和转角C。例题例题446.3叠加法确定梁的挠度与转角3.第二类叠加法——应用于间断性分布荷载作用的情形解：解：1.首先，将梁上的荷载变成有表可查的情形6.3叠加法确定梁的挠度与转角2．再将处理后的梁分解为简单荷载作用的情形，计算各个简单荷载引起的挠度和转角414322218112128482,,CCBBqlwEIlqlqllwwEIEIEIqlEIqlCC323148161,例题433．．将简单荷载作用的结果叠加,EIqlwwiCiC42138441＝EIqliCiC3214876.3叠加法确定梁的挠度与转角例题46.4梁的刚度问题第6章弯曲刚度对于主要承受弯曲的零件和构件，刚度设计就是根据对零件和构件的不同工艺要求，将最大挠度和转角（或者指定截面处的挠度和转角）限制在一定范围内，即满足弯曲刚度条件：w——许用挠度——许用转角均根据对于不同零件或构件的工艺要求而确定。1、弯曲刚度条件wwmaxmax6.4梁的刚度问题钢制圆轴，左端受力为FP，FP＝20kN，a＝lm，l＝2m，E=206GPa，其他尺寸如图所示。规定轴承B处的许用转角θ=0.5°。试求：根据刚度要求确定该轴的直径d。B例题例题556.4梁的刚度问题B解：1．查表确定B处的转角EIlaFB3P＝－由挠度表中查得承受集中荷载的外伸梁B处的转角为6.4梁的刚度问题2．根据刚度设计准则确定轴的直径B例题5BB其中，的单位为rad（弧度），而θ的单位为（°）（度），考虑到单位的一致性，将有关数据代入后，有5.0180102063642110201803493dEIalFPB6.4梁的刚度问题从而得到轴的直径mm111m1011.1m5.01020631806421102014293d例题5ABlqbh矩形截面悬臂梁承受均布载荷如图所示。已知q=10kN/m，l=3m，E=196GPa，[]=118MPa，许用最大挠度与梁跨度比值[wmax/l]=1/250，且已知截面高与宽之比为2，即h=2b。试：确定截面尺寸b和h。例题例题666.4梁的刚度问题6.4梁的刚度问题解：1.强度条件ABlqbhmkN45310102121232maxqlMmm8310118210453233633maxMbWMmaxmax223/62/62/3Wbhbbb2.刚度条件lwlwmaxmax4max8qlwEI312bhImm6.89101961625031010316349434max4lwEqlb896mm,b179mmh综合上述设计结果，取刚度设计所得到的尺寸,作为梁的最终尺寸,即例题66.5提高梁刚度的措施第6章弯曲刚度梁的变形除了与荷载与梁的约束有关外，还取决于以下因素：材料材料——梁的变形与弹性模量E成反比。截面截面——梁的变形与截面的惯性矩I成反比；跨长跨长——梁的变形与跨长l的n次幂成正比；1、提高梁刚度的措施6.5提高梁刚度的措施EIlFwB3P25632P7128AFlEI因此,减小弹性位移主要是减小梁的长度l。当梁的长度无法减小时，则可增加中间支座（即采用超静定结构）。减小跨长跨长跨长——梁的变形与跨长l的n次幂成正比；EIlFwB3P25632P7128AFlEI选择合理的截面形状截面的惯性矩I6.5提高梁刚度的措施例如，在车床上加工较长的工件时，为了减小切削力引起的挠度，以提高加工精度，可在卡盘与尾架之间再增加一个中间支架。减小跨长6.5提高梁刚度的措施此外，选用弹性模量E较高的材料也能提高梁的刚度。但是，对于各种钢材，弹性模量的数值相差甚微，因而与一般钢材相比，选用高强度钢材并不能提高梁的刚度。增大弹性模量6.5提高梁刚度的措施EIlFwB3P25632P7128AFlEI2、拓展到圆轴扭转和拉压情况类似地，提高受扭圆轴的刚度，也可以通过减小轴的长度、增加轴的扭转刚度（GIP）来实现。同样，对于各种钢材，切变模量G的数值相差甚微，所以通过采用高强度钢材以提高轴的扭转刚度，其效果是不明显的。6.5提高梁刚度的措施1nxiiiPiMlGIiiiiEAlFlNΔ6.6简单的静不定梁第6章弯曲刚度静不定次数：未知力个数与独立平衡方程数之差静定问题与静定结构：未知力（内力或外力）个数等于独立的平衡方程数静不定问题与静不定结构：未知力个数多于独立的平衡方程数多余约束：保持结构静定多余的约束6.6简单的静不定梁1、基本概念BAlq多余约束的存在2、求解静不定梁的基本方法使问题由静力学可解变为静力学不可解。由于多余约束对结构位移或变形有着确定的限制，而位移或变形又是与力相联系的，因而多余约束又为求解静不定问题提供了条件。6.6简单的静不定梁求解静不定问题，需要以下三方面的联立。3、物理方程（或称本构方程）：建立的力与位移或变形之间的关系。2、变形协调方程（或称为几何方程）：根据多余约束对位移或变形的限制，建立的各部分位移或变形之间的几何关系。1、平衡方程。6.6简单的静不定梁求：梁的约束力。已知：A端固定、B端铰支梁的弯曲刚度为EI，长度为l。6.6简单的静不定梁例题例题77BAlq解：1.确定静不定次数，并选择基本静定梁。多余约束的数目=16.6简单的静不定梁(2)简支梁(1)悬臂梁选择合适的多余约束，将其除去，使静不定结构变为静定结构，在解除约束处代之以约束力。化为静定结构的办法：一般来说，悬臂梁最为简单，其次是简支梁，最后为外伸梁。BAlqBlAqBlAqBFAM例题72.列出变形协调方程（几何方程）。根据基本静定梁的一切情况要与原超静定梁完全相同的要求，得到变形协调条件。0Bw0A6.6简单的静不定梁BAlqBlAqBFBlAqAM例题7(1)悬臂梁：3.根据物理方程（用积分法或叠加法求变形），列出补充方程，并求出多余未知力。仅有ｑ作用，B点挠度为：EIqlwBq84仅有作用，B点挠度为：ByFEIlFwBBF33因此BqBFBwwwEIql84EIlFB330解得：)(83qlFB6.6简单的静不定梁BlAqBF例题74.根据平衡方程在基本静定梁上求出其余的约束力。0xF,0AxF0yF),(85qlFAy0AM281qlMA（）6.6简单的静不定梁(1)悬臂梁：BlAqBFAxFAyFAM例题7(+)QF(-)ql85ql83l85M281ql21289ql因此2max81qlMqlFQ85maxqlFQmax2max21qlM5.在基本静定梁上按照静定梁的方法求解内力、应力和变形。6.6简单的静不定梁BlAqBFAxFAyFAM例题7BlAq处理具体问题时的注意点讨论：讨论：求解简单静不定求解简单静不定梁的步骤梁的步骤◆确定静不定次数，并选择基本静定梁。◆列出变形协调方程。◆根据物理方程（用积分法或叠加法求变形），列出补充方程，并求出多余未知力。◆根据平衡方程在基本静定梁上求出其余的约束反力。◆在基本静定梁上按照静定梁的方法求解内力、应力和变形。力法：以力作为未知量,将位移表示为力的形式，从而求解未知力，进而求解位移的方法。BAlq梁AB和BC在B处铰接，A、C两端固定，梁的抗弯刚度均为EI，F=40kN，q=20kN/m。画梁的剪力图和弯矩图。例题例题886.6简单的静不定梁解：１、从B处拆开，使超静定结构变成两个悬臂梁。２、变形协调方程为：21BBwwBBFFFBMMAAFFAAyB1F'BMMCCFFCCyB2３、物理方程EIFEIqwBB3484341EIFEIFw'BB34243623226.6简单的静不定梁例题8FBFBMMAAFFAAMMCCFFCCyB1yB2kN75.84842046104023342BF代入变形协调方程：EIFEIFEIFEIqBB342436234843234４、平衡方程确定A端约束力04,0qFFFBAykN25.7175.82044BAFqF0424,0BAAFqMMmkN12575.842204424BAFqM6.6简单的静不定梁例题8FBF´BMMAAFFAAMMCCFFCCyB1yB20,0FFFFCBy确定C端约束力kN75.4875.840BCFFF042,0BCCFFMMkN.m11540275.8424FFMBC6.6简单的静不定梁例题8MMAAFFAAMMCCFFCCA、B端约束力已求出５、最后作梁的剪力图和弯矩图)()(25.7175.875.48kNQF)(kN25.71AF)kN(75.48CF)(mkN125AM)m(kN115CM6.6简单的静不定梁)(1251155.17)mkN(M)(例题8课外作业P168－169：6－2(c)，6－4，6－5（补充），6－6(a)P170－171：6－10，6－11补充习题1，补充习题2P323：12－17NanjingUniversityofTechnology