截面惯性矩(材料力学),截面惯性矩材料力学



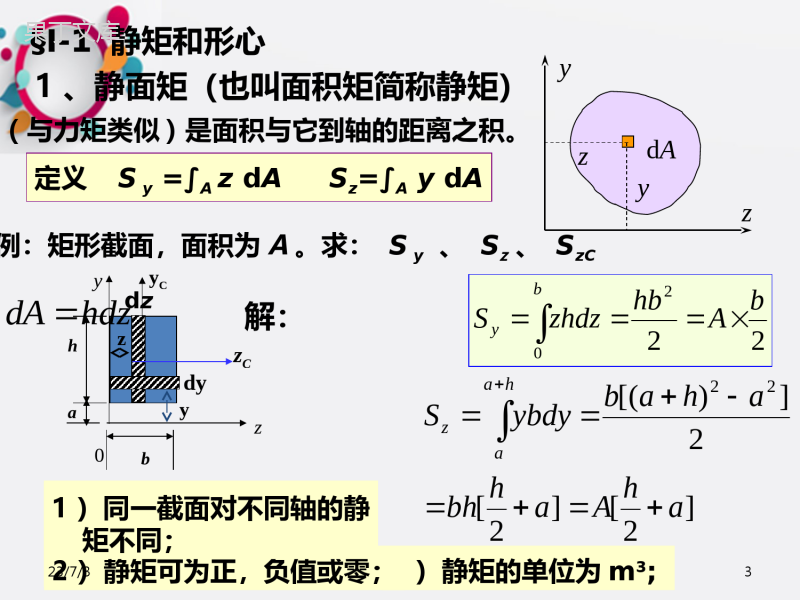
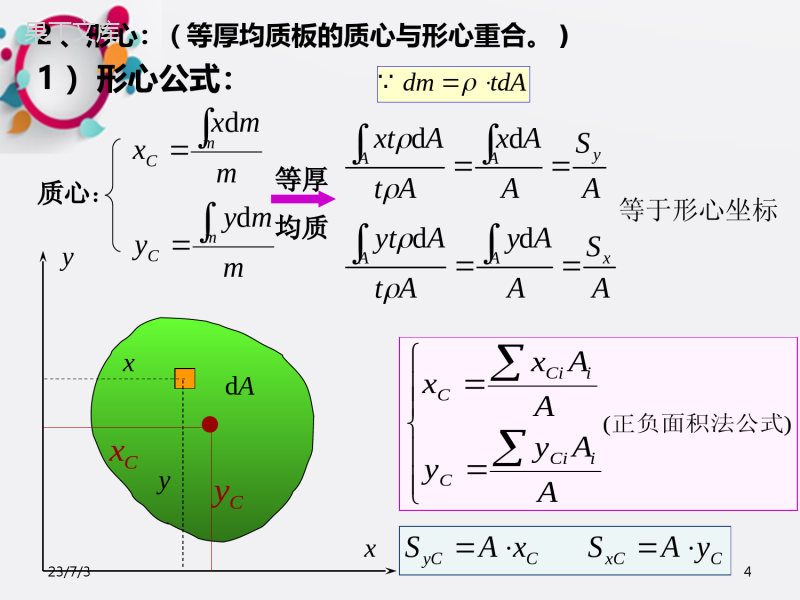
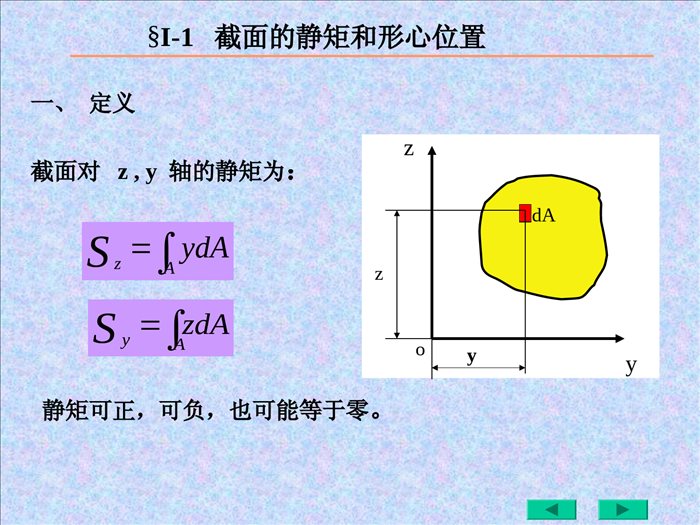
4.4.构件的强度计构件的强度计算算23/7/314.14.1截面的几何特截面的几何特征征§Ⅰ-4的平行移轴公式§Ⅰ-2§Ⅰ-2惯性矩和惯性半径惯性矩和惯性半径§Ⅰ-3§Ⅰ-3惯性积惯性积§Ⅰ-2§Ⅰ-2惯性矩和惯性半径惯性矩和惯性半径§Ⅰ-3惯性积§Ⅰ-2惯性矩和惯性半径23/7/32dzyz0hab定义Sy=∫AzdASz=∫AydA例:矩形截面,面积为A。求:Sy、Sz、SzC解:dy(与力矩类似)是面积与它到轴的距离之积。dAzyyz2220bAhbzhdzSby]2[]2[2])[(22ahAahbhahabybdyShaaz1、静面矩(也叫面积矩简称静矩)zyzCyChdzdA§Ⅰ-1静矩和形心1)同一截面对不同轴的静矩不同;2)静矩可为正,负值或零;3)静矩的单位为m3;1)同一截面对不同轴的静矩不同;2)静矩可为正,负值或零;1)同一截面对不同轴的静矩不同;3)静矩的单位为m3;2)静矩可为正,负值或零;1)同一截面对不同轴的静矩不同;23/7/331)形心公式:2、形心:(等厚均质板的质心与形心重合。))(正负面积法公式AAyyAAxxiCiCiCiCdAxyyx等厚均质mmyymmxxmCmCdd质心:ASAAyAtAytASAAxAtAxtxAAyAAdddd等于形心坐标CxCytdAdmCxCCyCyASxAS23/7/34ACiiCyxdAxAAxSAxdAxAydAyACACAyAyAxAxiiCiiCACiiCxydAyAAyS3.结论当坐标轴过形心时,图形对自身形心轴的面积矩等于零;反之,若图形对某轴的面矩为零时,此轴必过图形的形心。2.形心公式23/7/353.组合图形的形心和面积矩1)组合图形由简单图形(如三角形,圆形,矩形等)组合而成的图形。2)组合图形面积矩及形心的计算公式等于各简单图形对同一轴的面积矩的代数和。即CiiAnAAZnZZZyAydAydAydASSSS......2121iniCiiiyCiniCiiizCAZAASZAyAASy1123/7/36例1:求图示T形截面的形心及对z轴的静矩选坐标轴z1作为参考轴方法3)负面积法Sz=(12010060)-2(1004050)=32104mm31.求形心mm302201006010020CySz=(50+30)2(10020)=32104mm3方法2)不求形心Sz=AiyCi=20100110+2010050=32iniCiiCAyAy1知A=A1+A2yC1=60yC2=02、求静矩iCzAyS方法1)z1zC2020100y100••••BⅠⅡzyC123/7/37§I-2惯性矩、惯性积、极惯性矩1、惯性矩:(惯性矩是一个物理量,通常被用作描述一个物体抵抗扭动,扭转的能力)AyAxAxIAyIdd22dAxyyx它是图形面积与它对轴的距离的平方之积表达式为注意:1)同一截面对不同的轴惯性矩不同;2)惯性矩永远为正值;3)惯性矩的单位为m4;23/7/383、极惯性矩:APAId2它是图形面积对极点的二次矩。2、惯性半径(单位为m)表达式为AIiAIiyyxxdAxyyxAxyPIIdAyxIyx)(22222yxPIII图形对正交坐标轴的惯性矩之和等于它对此二轴交点的极惯性矩23/7/39zyo例求圆形截面对形心轴的惯性矩。32242022DddAIDAP00zyPIII解:§I-3惯性积1.定义:图形对两个坐标轴的两个坐标之积的积分。642400DIIIPzy23/7/310§I-3惯性积2.表达式:AyzyzdAI3.说明:1)同一图形对不同轴的惯性积不同;2)惯性积可正,可负,可为零。3)惯性积的单位:m44.结论:当坐标系的两轴中的任一轴为图形的对称轴时,图形对此轴的惯性积为零,反之,若图形对坐标系的惯性积为零时,此坐标轴中必有一轴为图形的对称轴。zyA2A1bbh23/7/311返1.平行移轴定理:CCybyxax以形心为原点,建立与原坐标轴平行的坐标轴如图0CxCAySAbbyyAbyAyICACACAxd)2(d)(d2222AbIIxCx2dAxyyxabCxCyC§Ⅰ-4平行移轴公式AbbSIxCxC2223/7/312r§Ⅰ-4平行移轴公式2.结论:abAIIAbIIAaIIxCyCxyxCxyCy22B)当图形至少有一条轴是图形的对称轴时,则有A)在所有的平行轴中,图形对自身形心轴的惯性矩为最小。0xCyCxyIabAIdAxyyxabCxCyC23/7/313例组合截面惯性矩的计算,求截面对ZC轴的惯性矩。5332221067.16121002012hbIz452523222212111034.532000301067.162000301067.66)()(mmAaIAaIIzzzC2212120001002030301020mmAAmmamma返回3331111067.66122010012hbIz2020100zy100••••A2ⅠⅡz2zc30z1A1解:1)写出A1,A2及其形心坐标a1;a22)求出A1和A2分别对自身形心轴的惯性矩3)求对整个截面形心ZC轴的惯性矩a1a223/7/314dAzzzyz1z1y1z1§I-5转轴公式及主惯性矩(简介)1.转轴公式:当坐标轴绕原点转一个角度后,得到一个新的坐标轴时,转轴公式给出在新旧坐标轴下的惯矩及惯积的关系.sincossincos11yzzzyy2sinsincos)sincos(222211yzzyAAzIIIdAzydAyI22cos1sin22cos1cos2223/7/3152cos2sin22sin2cos222sin2cos221111yzZyZYyzZyZyZyzZyZyyIIIIIIIIIIIIIIII2)主惯性矩:相对主轴的惯性矩就称为主惯性矩.2.三个公式:设新坐标系由原坐标系逆转α角而得,且有2sin2cos221yzZyZyZIIIIII3.主轴及主惯性矩:1)主轴:图形若对坐标轴的惯矩为零时,这对坐标轴就称为主轴.且当主轴为形心轴时,就称为形心主轴.用α0来表示主轴的方向.23/7/316杆件的拉压变形及强度计算杆件的拉压变形及强度计算23/7/317目录一、概述二、杆件的轴向拉压变形分析三、材料在拉伸和压缩时的力学性质四、拉(压)杆的强度计算杆件的拉压变形及强度计算杆件的拉压变形及强度计算23/7/318古代建筑结构建于唐末(857年)的山西五台山佛光寺东大殿一、概述23/7/319古代建筑结构建于辽代(1056年)的山西应县佛宫寺释迦塔塔高9层共67.31米,用木材7400吨900多年来历经数次地震不倒,现存唯一木塔23/7/320古代建筑结构2200年以前建造的都江堰安澜索桥23/7/321古代建筑结构建于隋代(605年)的河北赵州桥桥长64.4米,跨径37.02米,用石2800吨23/7/322二桥梁结构23/7/323航空航天23/7/324强度:即抵抗破坏的能力刚度:即抵抗变形的能力稳定性:即保持原有平衡状态的能力构件的强度、刚度和稳定性不仅与构件的形状有关,而且与所用材料的力学性能有关,因此在进行理论分析的基础上,实验研究是完成材料力学的任务所必需的途径和手段。构件的承载能力23/7/325四川彩虹桥坍塌23/7/326美国纽约马尔克大桥坍塌23/7/327拉压变形拉(压)、剪切、扭转、弯曲剪切变形杆件的基本变形:23/7/328扭转变形弯曲变形23/7/329二、杆件的轴向拉压变形分析23/7/330一、轴向拉伸和压缩的概念23/7/33123/7/33223/7/33323/7/334特点:作用在杆件上的外力合力的作用线与杆件轴线重合,杆件变形是沿轴线方向的伸长或缩短。杆的受力简图为FF拉伸FF压缩23/7/33523/7/336FF1、轴力:横截面上的内力2、截面法求轴力mmFFN切:假想沿m-m横截面将杆切开留:留下左半段或右半段代:将抛掉部分对留下部分的作用用内力代替平:对留下部分写平衡方程求出内力即轴力的值0xFFFN0FFNFFN二、拉伸和压缩时的内力、截面法和轴力23/7/3373、轴力正负号:拉为正、压为负4、轴力图:轴力沿杆件轴线的变化由于外力的作用线与杆件的轴线重合,内力的作用线也与杆件的轴线重合。所以称为轴力。FFmmFFN0xFFFN0FFNFFN23/7/338轴力和轴力图已知F1=10kN;F2=20kN;F3=35kN;F4=25kN;试画出图示杆件的轴力图。110xFkN1011FFN例题3-1FN1F1解:1、计算各段的轴力。F1F3F2F4ABCDAB段kN102010212FFFNBC段2233FN3F4FN2F1F2122FFFN0xF0xFkN2543FFNCD段2、绘制轴力图。kNNFx10251023/7/339三、应力概念、拉(压)杆横截面上的应力杆件的强度不仅与轴力有关,还与横截面面积有关。必须用应力来比较和判断杆件的强度。23/7/340——横截面上的应力23/7/341——横截面上的应力23/7/342——横截面上的应力AFN该式为横截面上的正应力σ计算公式。正应力σ和轴力FN同号。即拉应力为正,压应力为负。根据杆件变形的平面假设和材料均匀连续性假设可推断:轴力在横截面上的分布是均匀的,且方向垂直于横截面。所以,横截面的正应力σ计算公式为:23/7/343•拉(压)杆横截面上的应力AFNσ=MPaFN表示横截面轴力(N)A表示横截面面积(mm2)FFmmnnFFN23/7/344——横截面上的应力23/7/345截面上的应力例题3-2图示结构,试求杆件AB、CB的应力。已知F=20kN;斜杆AB为直径20mm的圆截面杆,水平杆CB为15×15的方截面杆。FABC0yFkN3.281NF解:1、计算各杆件的轴力。(设斜杆为1杆,水平杆为2杆)用截面法取节点B为研究对象kN202NF0xF45°045cos21NNFF045sin1FFN12FBF1NF2NFxy45°23/7/346截面上的应力kN3.281NFkN202NF2、计算各杆件的应力。MPa90Pa109010204103.286623111AFNMPa89Pa1089101510206623222AFNFABC45°12FBF1NF2NFxy45°23/7/347三、材料在拉伸和压缩时的力学性质教学目标:1.拉伸、压缩试验简介;2.应力-应变曲线分析;3.低碳钢与铸铁的拉、压的力学性质;4.试件的伸长率、断面收缩率计算。教学重点:1.应力-应变曲线分析;2.材料拉、压时的力学性质。教学难点:应力-应变曲线分析。小结:塑性材料与脆性材料拉伸时的应力-应变曲线分析。作业:复习教材相关内容。23/7/3481、材料拉伸时的试件力学性质:在外力作用下材料在变形和破坏方面所表现出的力学性能试件和实验条件常温、静载§2-423/7/3492、材料拉伸时的设备23/7/3503、材料拉伸时的应力-应变曲线低碳钢的拉伸23/7/351oabcef明显的四个阶段1、弹性阶段ob—P比例极限E—e弹性极限tanE2、屈服阶段bc(失去抵抗变形的能力)—s屈服极限3、强化阶段ce(恢复抵抗变形的能力)强度极限—b4、局部径缩阶段efPesb23/7/352材料拉伸时的两个塑性指标两个塑性指标:%100001lll断后伸长率断面收缩率%100010AAA%5为塑性材料%5为脆性材料低碳钢的%3020—%60为塑性材料023/7/3534.卸载定律及冷作硬化卸载定律及冷作硬化1、弹性范围内卸载、再加载oabcefPesb2、过弹性范围卸载、再加载ddghf即材料在卸载过程中应力和应变是线形关系,这就是卸载定律。材料的比例极限增高,延伸率降低,称之为冷作硬化或加工硬化。23/7/3545、其他材料拉伸时的力学性质其它材料拉伸时的力学性质对于没有明显屈服阶段的塑性材料,用名义屈服极限σp0.2来表示。o%2.02.0p23/7/3556、铸铁材料拉伸时的力学性质obt对于脆性材料(铸铁),拉伸时的应力应变曲线为微弯的曲线,没有屈服和颈缩现象,试件突然拉断。断后伸长率约为0.5%。为典型的脆性材料。σbt—拉伸强度极限(约为140MPa)。它是衡量脆性材料(铸铁)拉伸的唯一强度指标。23/7/3567、材料压缩时的力学性质试件和实验条件常温、静载§2-523/7/3578、塑性材料压缩时的力学性质塑性材料(低碳钢)的压缩屈服极限—S比例极限—p弹性极限—e拉伸与压缩在屈服阶段以前完全相同。E---弹性摸量23/7/3589、脆性材料压缩时的力学性质脆性材料(铸铁)的压缩obtbc脆性材料的抗拉与抗压性质不完全相同压缩时的强度极限远大于拉伸时的强度极限btbc23/7/35923/7/360四、拉(压)杆的强度计算教学目标:1.许用应力和安全系数;2.拉、压杆的强度条件;3.拉、压杆的变形计算。教学重点:1.拉、压杆的强度校核;2.杆件截面尺寸设计。教学难点:拉、压杆的变形量计算。小结:杆件强度校核及尺寸设计。23/7/361•许用应力和安全系数极限应力:材料丧失正常工作能力时的应力。塑性变形是塑性材料破坏的标志。屈服点为塑性材料的极限应力。断裂是脆性材料破坏的标志。因此把抗拉强度和抗压强度,作为脆性材料的极限应力。sbby许用应力:构件安全工作时材料允许承受的最大应力。构件的工作应力必须小于材料的极限应力。塑性材料:ssn[]=脆性材料:[]=bbnns、nb是安全系数:ns=1.2~2.5nb=2.0~3.51.许用应力和安全系数五、拉(压)杆的强度计算23/7/3622、拉压杆的强度条件AFNmaxAFNmax根据强度条件,可以解决三类强度计算问题1、强度校核:NFA2、设计截面:AFN3、确定许可载荷:23/7/363拉压杆的强度条件例题3-30yF解:1、研究节点A的平衡,计算轴力。N1032.520cos2101000cos253FFN由于结构几何和受力的对称性,两斜杆的轴力相等,根据平衡方程F=1000kN,b=25mm,h=90mm,α=200。〔σ〕=120MPa。试校核斜杆的强度。FFbhABC0cos2NFF得A2、强度校核由于斜杆由两个矩形杆构成,故A=2bh,工作应力为MPa120MPa2.118P102.11810902521032.52665abhFAFNN斜杆强度足够FxyNFNF23/7/364拉压杆的强度条件例题3-4D=350mm,p=1MPa。螺栓[σ]=40MPa,求直径。pDF24π每个螺栓承受轴力为总压力的1/6解:油缸盖受到的力根据强度条件AFNmax22.6mmm106.22104061035.0636622pDd即螺栓的轴力为pDFFN224π6NFA得24422pDd即螺栓的直径为Dp23/7/365拉压杆的强度条件例题3-5AC为50×50×5的等边角钢,AB为10号槽钢,〔σ〕=120MPa。求F。0yFFFFN2sin/1解:1、计算轴力。(设斜杆为1杆,水平杆为2杆)用截面法取节点A为研究对象FFFNN3cos120xF0cos21NNFF0sin1FFN2、根据斜杆的强度,求许可载荷kN6.57N106.57108.4210120212134611AFAF1NF2NFxyα查表得斜杆AC的面积为A1=2×4.8cm211AFN23/7/366拉压杆的强度条件FFFN2sin/1FFFNN3cos123、根据水平杆的强度,求许可载荷kN7.176N107.1761074.12210120732.113134622AFAF1NF2NFxyα查表得水平杆AB的面积为A2=2×12.74cm222AFN4、许可载荷kN6.57176.7kNkN6.57minminiFF23/7/367六、拉压杆的变形虎克定律一纵向变形AFllEAlFlNE二横向变形llbbb1bb钢材的E约为200GPa,μ约为0.25—0.33E为弹性摸量,EA为抗拉刚度泊松比横向应变AFN23/7/368拉压杆的变形虎克定律23/7/369拉压杆的变形虎克定律23/7/370拉(压)杆的变形1.绝对变形:规定:L—等直杆的原长d—横向尺寸L1—拉(压)后纵向长度d1—拉(压)后横向尺寸轴向变形:LLL1横向变形:ddd1拉伸时轴向变形为正,横向变形为负;压缩时轴向变形为负,横向变形为正。轴向变形和横向变形统称为绝对变形。23/7/371拉(压)杆的变形2.相对变形:单位长度的变形量。LL=-dd和′都是无量纲量,又称为线应变,其中称为轴向线应变,′称为横向线应变。3.横向变形系数:′=/23/7/372•虎克定律:实验表明,对拉(压)杆,当应力不超过某一限度时,杆的轴向变形与轴力FN成正比,与杆长L成正比,与横截面面积A成反比。这一比例关系称为虎克定律。引入比例常数E,其公式为:EALFLNE为材料的拉(压)弹性模量,单位是GPaFN、E、A均为常量,否则,应分段计算。由此,当轴力、杆长、截面面积相同的等直杆,E值越大,就越小,所以E值代表了材料抵抗拉(压)变形的能力,是衡量材料刚度的指标。L或E23/7/373例题3-6:如图所示杆件,求各段内截面的轴力和应力,并画出轴力图。若杆件较细段横截面面积,较粗段,材料的弹性模量,求杆件的总变形。21200mmA22300mmAGPaE200mmL100LL10KN40KN30KNABC解:分别在AB、BC段任取截面,如图示,则:FN1=10KN10KNFN110KNσ1=FN1/A1=50MPa30KNFN2FN2=-30KNσ2=FN2/A2=100MPa轴力图如图:xFN10KN30KN23/7/374由于AB、BC两段面积不同,变形量应分别计算。由虎克定律:EALFLN可得:LAB10KNX100mm200GPaX200mm2==0.025mmLBC-30KNX100mm200GPaX300mm2==-0.050mmL=-0.025mm23/7/375例题3-7AB长2m,面积为200mm2。AC面积为250mm2。E=200GPa。F=10kN。试求节点A的位移。0yFkN202sin/1FFFN解:1、计算轴力。(设斜杆为1杆,水平杆为2杆)取节点A为研究对象kN32.173cos12FFFNN0xF0cos21NNFF0sin1FFN2、根据胡克定律计算杆的变形。1mmm101102001020021020369311111AElFlNAF1NF2NFxy300拉压杆的变形胡克定律mm6.0m106.01025010200732.11032.17369322222AElFlN斜杆伸长水平杆缩短23/7/376七、应力集中的概念常见的油孔、沟槽等均有构件尺寸突变,突变处将产生应力集中现象。即mtKmax称为理论应力集中因数1、形状尺寸的影响:尺寸变化越急剧、角越尖、孔越小,应力集中的程度越严重。2、材料的影响:应力集中对塑性材料的影响不大;应力集中对脆性材料的影响严重,应特别注意。23/7/377谢谢!!谢谢!!!!23/7/378
提供截面惯性矩(材料力学),截面惯性矩材料力学会员下载,编号:1701026991,格式为 xlsx,文件大小为78页,请使用软件:wps,office Excel 进行编辑,PPT模板中文字,图片,动画效果均可修改,PPT模板下载后图片无水印,更多精品PPT素材下载尽在某某PPT网。所有作品均是用户自行上传分享并拥有版权或使用权,仅供网友学习交流,未经上传用户书面授权,请勿作他用。若您的权利被侵害,请联系963098962@qq.com进行删除处理。

 下载
下载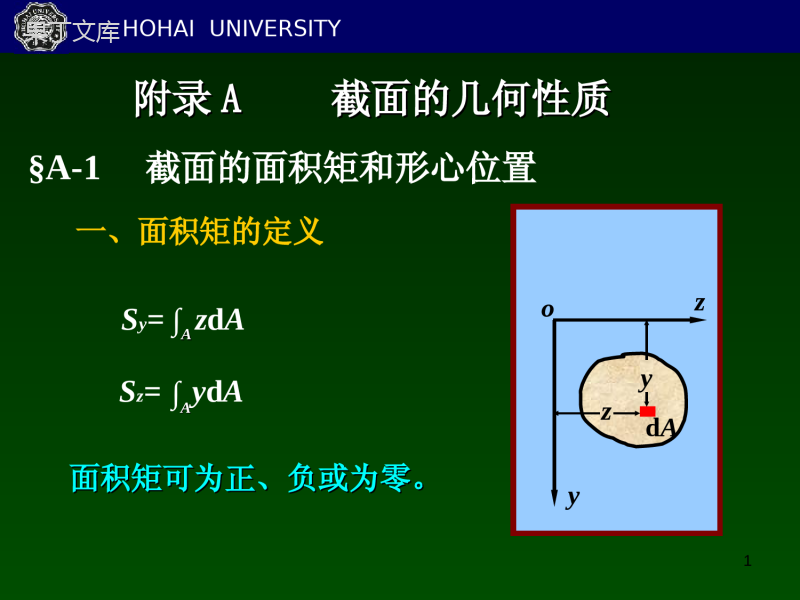 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载