自动控制原理与系统--课件第五章自动控制系统的校正

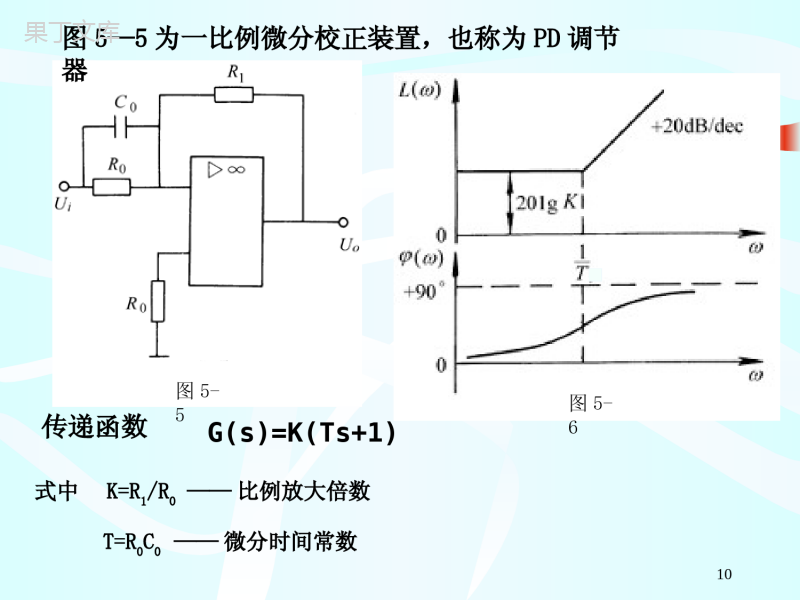
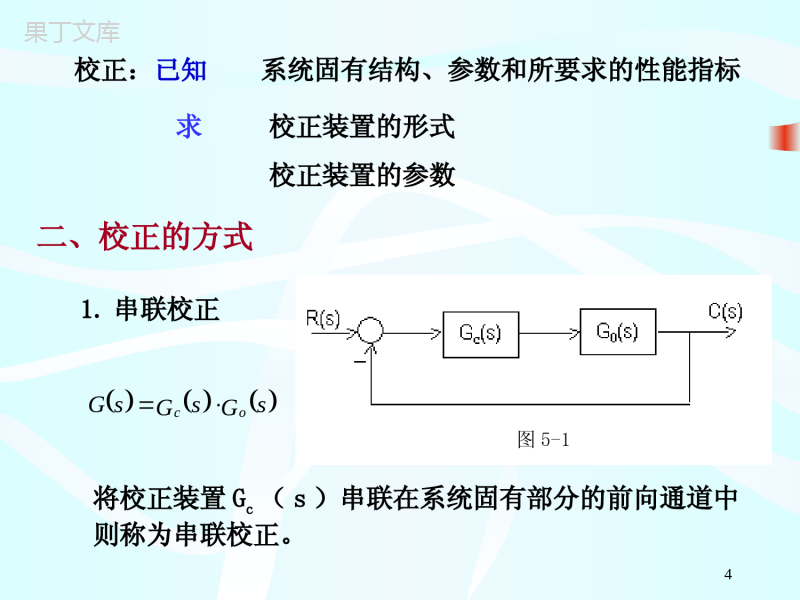
1第五章控制系统的校正与设计2•自动控制系统的主要任务就是实现对被自动控制系统的主要任务就是实现对被控对象的控制。控对象的控制。系统的执行元件、比较元件、放大元件和测量元件等，除放大元件的放大系数可作适当调整以外，其它元件的参数基本上是固定不变的，称为系统的固有部分。根据被控对象的工作条件、技术要求、工艺要求、经济性要求以及可靠性要求等提出控制系统的性能指标。第一节校正的基本概念一、校正的概念3•当控制系统的性能指标不能满足实际工程所提出的要求时,为了使控制系统满足性能指标，就必须在系统固有部分的基础之上增加一些装置和元件,称之为校正装置或校正元件校正装置或校正元件。•加入校正装置或校正元件改善系统性能，并满足系统性能指标要求的方法，称为系统校正校正。4校正：已知系统固有结构、参数和所要求的性能指标求校正装置的形式校正装置的参数1.串联校正将校正装置Gc（s）串联在系统固有部分的前向通道中则称为串联校正。图5-1sGsGsGoc二、校正的方式52、反馈校正图5-2将校正装置Gc（s）与需要校正的环节作反馈连接称为反馈校正。63．复合校正图5-3复合校正是在反馈校正的基础上，引入输入补偿构成的校正方式。一种是给定输入信号补偿，另一种是扰动输入信号补偿。7三、校正装置1、无源校正装置相位滞后相位超前相位滞后-超前图5-4优点：无源校正装置线路简单、组合方便、无需外供电源缺点：本身没有增益，只有衰减；输入阻抗低，输出阻抗高，因此在应用时要增设放大器或隔离放大器。组成：由电阻、电容构成的二端口网络82、有源校正装置优点：本身有增益，输入阻抗高，输出阻抗低缺点：需另供电源组成：运算放大器（目前较多使用）超前9第二节串联校正一、三频段对系统性能的影响二、串联校正方法1、比例微分校正（相位超前校正）代表参数对系统性能的影响低频段斜率和高度反映系统的型别和增益。表明了系统的稳态精度。中频段斜率、宽度（中频宽）、幅值穿越频率和相位裕量反映系统的最大超调量和调整时间。表明了系统的相对稳定性和快速性。高频段斜率反映系统对高频干扰信号的衰减能力。10传递函数G(s)=K(Ts+1)式中K=R1/R0——比例放大倍数T=R0C0——微分时间常数图5-5图5-6图5—5为一比例微分校正装置，也称为PD调节器11例5-1设图5-7所示系统的开环传递函数为)1)(1()(21sTsTsKsG其中T1=0.2，T2=0.01，K=35，采用PD调节器（K=1,T=0.2s），对系统作串联校正。试比较系统校正前后的性能。解：原系统的Bode图如图5-8中曲线I所示。特性曲线以-40dB/dec的斜率穿越0dB线，穿越频率ωc=13.5dB，相位裕量γ=12.3o。采用PD调节器校正，其传递函数Gc(s)=0.2s+1，Bode图为图5-8中的曲线II。图5—712图5—13由图可见，增加比例微分校正装置后：在低频段，L(ω)的斜率和高度均没变，所以不影响系统的稳态精度。在中频段，L(ω)的斜率由校正前的-40dB/dec变为校正后的-20dB/dec，相位裕量由原来的13.5o提高为70.7o，提高了系统的相对稳定性；穿越频率ωc由13.2变为35，快速性提高。在高频段，L(ω)的斜率由校正前的-60dB/dec变为校正后的-40dB/dec，系统的抗高频干扰能力下降。综上所述，比例微分校正不影响系统的稳态精度综上所述，比例微分校正不影响系统的稳态精度,,将使系统的稳定性和快速性改善，但是抗高频干扰能将使系统的稳定性和快速性改善，但是抗高频干扰能力下降。力下降。串联比例微分校正一般用于系统稳态性能已满足串联比例微分校正一般用于系统稳态性能已满足要求要求,,但动态性能有待改善的系统。但动态性能有待改善的系统。142.比例积分校正（相位滞后校正）图5-9传递函数式中KC=R1/R0——比例放大倍数Tc=R1C1——积分时间常数sTsTKsGCCCC)1()(图5—9为一比例积分校正装置，也称为PI调节器CC15例5-2设图5-11所示系统的固有开环传递函数为)1)(1()(211sTsTKsG其中T1=0.33，T2=0.036，K1=3.2。采用PI调节器（K=1.3,T=0.33s），对系统作串联校正。试比较系统校正前后的性能。图5-1116解：原系统的Bode图如图5-12中曲线I所示。特性曲线低频段的斜率为0dB，显然是有差系统。穿越频率ωc=9.5dB，相位裕量γ=88o。采用PI调节器校正，其传递函数sssGC33.0)133.0(3.1)(Bode图为图5-12中的曲线Ⅱ。校正后的曲线如图5-12中的曲线Ⅲ。由图可见，增加比例积分校正装置后：在低频段，L(ω)的斜率由校正前的0dB/dec变为校正后的-20dB/dec，系统由0型变为I型，系统的稳态精度提高。在中频段，L(ω)的斜率不变，但由于PI调节器提供了负的相位角，相位裕量由原来的88o减小为65o，降低了系统的相对稳定性；穿越频率ωc有所增大，快速性略有提高。在高频段，L(ω)的斜率不变，对系统的抗高频干扰能力影响不大。因此，比例积分校正可以使系统的稳态精度得到明显改善，但使系统的稳定性变差。17图5-1218第三节反馈校正一、反馈校正的方式主体传递函数在系统中的作用硬反馈校正比例环节（可能还含有小惯性环节）Gc(s)=α（常数）在系统的动态和稳态过程中都起反馈校正作用软反馈校正微分环节（可能还含有小惯性环节）Gc(s)=αs只在系统的动态过程中起反馈校正作用，而在稳态时，反馈校正支路如同断路，不起作用19二、反馈校正的作用在图5－13中，设固有系统被包围环节的传递函数为G2(s)，反馈校正环节的传递函数为GC(s)，则校正后系统被包围部分传递函数变为)()(1)(2212sGsGsGXXC反馈校正可以改变系统被包围环节的结构和参数，使系统的性能达到所要求的指标。图5－1320图5－13对系统的比例环节G2(s)=K进行局部反馈•当采用硬反馈，即GC(s)=α时，校正后的传递函数为KKsG1)(K11增益降低环节，采用硬反馈是一种有效的方法。环节，采用硬反馈是一种有效的方法。倍，对于那些因为增益过大而影响系统性能的对于那些因为增益过大而影响系统性能的比例环节变为惯性环节，惯性环节时间常数为αK，动态过程变得平缓。对于希望过渡过程平缓的系统，经常采用软反馈。对于希望过渡过程平缓的系统，经常采用软反馈。•当采用软反馈，即GC(s)=αs时，校正后的传递函数为KsKsG1)(21对系统的积分环节G2(s)=K/s进行局部反馈•当采用硬反馈，即GC(s)=α时，校正后的传递函数为11/1)(sKKsKsG含有积分环节的单元，被硬反馈包围后，积分环节变为惯性环节，惯性环节时间常数为1/（αK），增益变为1/α。有利于系统的稳定，但稳态性能变差。图5－1322对系统的积分环节G2(s)=K/s进行局部反馈•当采用软反馈，即GC(s)=αs时，校正后的传递函数为sKkKsKsG)1(1/)(仍为积分环节，增益降为1/（1+αK）。有利于系统的稳定。图5－1323对系统的惯性环节G2(s)=K/(Ts+1)进行局部反馈•当采用硬反馈，即GC(s)=α时，校正后的传递函数为11)1/(1)(sKTKKKTsKsG惯性环节时间常数和增益均降为1/（1+αK）。可以提高系统的稳定性和快速性。图5－1324对系统的惯性环节G2(s)=K/(Ts+1)进行局部反馈•当采用软反馈，即GC(s)=αs时，校正后的传递函数为1)()(sKTKsG仍为惯性环节，时间常数增加为（T+αK）。图5－1325当G2(s)GC(s)》1时，)(1)()(1)(2212sGsGsGsGXXCC被包围环节的特性主要由校正环节决定，被包围环节的特性主要由校正环节决定，如果系统不可变部分的特性G2（s）是不希望的，可以通过适当选择反馈通道的传递函数Gc（s），使被包围环节的特性具有需要的特性，从而改善系统的性能。图5－1326第四节复合校正一、按输入补偿的复合校正C(s)=G1(s)G2(s)〔R(s)-C(s)+Gr(s)R(s)〕整理得)()()(1)()()(1)(2121sRsGsGsGsGsGsCr误差)()(1)()()(1)()()(2121sGsGsGsGsGsCsRsEr如果满足1-Gr(s)G1（s）G2(s)=0，则系统完全复现输入信号（即E(s)=0）,从而实现输入信号的全补偿。图5－1427二、按扰动补偿的复合校正图5－15不考虑输入控制，即R(s)=0时，扰动作用下的误差为)()()(1)()()()()()()(1)()()()()()(1)()()()()(212122121212sDsGsGsGsGsGsGsDsGsGsGsGsGsDsGsGsGsCsCsRsEdd如果满足1+Gd(s)G1(s)=0，即Gd(s)=-1/G1(s)时，则系统因扰动而引起的误差已全部被补偿（即E(s)=0）。28•要实现全补偿是很困难的，但可以实现近似的全补偿，能够大幅度地减小扰动误差，显著地改善系统的动态和稳态性能。因此按扰动补偿的复合校正在要求较高的控制场合得到广泛应用。295.5典型系统一般来说，控制系统的开环传递函数可以表示为)1)(1()1)(1()(2121sssssKsGvgg分母中的sv项表示该系统在原点处有v个重极点，或者说，系统含有v个积分环节。根据v=0，1，2，……等不同数值，分别称作0型、I型、Ⅱ型、……系统。30自动控制理论已经证明，0型系统稳态精度低，而Ⅲ型和高于Ⅲ型的系统很难稳定。因此，为了保证稳定性和较好的稳态精度，多选用I型和II型系统。315.5.1典型I型系统1.典型Ⅰ型系统的数学模型式中T—系统的惯性时间常数；K—系统的开环增益。)1(ssKg)(sR)(sC)1()(TssKsGT(K＜1/T)32开环对数频率特性dB/L0g1-1/sω20090-1/sωc图3-13典型I型系统开环对数频率特性18013540T)1()(TssKsG33典型的I型系统结构简单，其对数幅频特性的中频段以–20dB/dec的斜率穿越0dB线，只要参数的选择能保证足够的中频带宽度，系统就一定是稳定的，且有足够的稳定裕量，即选择参数满足T1c于是，相角稳定裕度459090180TTccarctgarctg34•K与截止频率c的关系当c<1/T时，特性以–20dB/dec斜率穿越零分贝线，系统有较好的稳定性。由图中的特性可知clg201lg20lg20cK所以K=c（当c时）T1(3-18)352.开环放大系数和动态性能指标的关系典型I型系统的开环传递函数如式所示，它包含两个参数：开环增益K和时间常数T。其中，时间常数T在实际系统中往往是控制对象本身固有的，能够由调节器改变的只有开环增益K，也就是说，K是唯一的待定参数。设计时，需要按照性能指标选择参数设计时，需要按照性能指标选择参数KK的大小的大小。。)1()(TssKsG(K＜1/T)36典型I型系统的闭环传递函数为开环放大系数K和性能指标的关系TKsTsTKTssKTssKsG1/)1(1)1()(2cl典型I型系统是一个二阶系统，而二阶系统传递函数的标准形式为2222)(nnnclsssG37•K、T与标准形式中的参数的换算关系TKnKT121T21n且有38•二阶系统的性质当<1时，系统动态响应是欠阻尼的振荡特性；当1时，系统动态响应是过阻尼的单调特性；当=1时，系统动态响应是临界阻尼。由于过阻尼特性动态响应较慢，所以一般常把系统设计成欠阻尼状态，即0<<139由于在典型I系统中KT<1，得>0.5。因此在典型I型系统中应取欠阻尼二阶系统在零初始条件下的阶跃响应动态指标计算公式15.040%100e%)1/π(2)arccosπ(122rTt超调量上升时间调节时间ns3tns4t(±5%)(±2%)41典型I型系统不同K值下的性能指标具体选择参数时，应根据系统工艺要求选择参数以满足性能指标。在工程设计中,为使系统既有较好的相对稳定性,又有较快的响应，通常取K=1/2T(对应ζ=0.707)，即为“二阶最佳二阶最佳”系统。T41T56.21T21T44.11T1开环放大系数K阻尼比ζ超调量σ%相角裕量γ(ωc)上升时间tr1.0076.3º∞0.81.5%69.9º6.67T0.7074.3%65.5º4.72T0.69.5%59.2º3.34T0.516.3%51.8º2.41T说明快速性与稳定性之间的矛盾。在具体选择参数K时，须在二者之间取折衷。425.5.2典型Ⅱ型系统1.典型Ⅱ型系统的数学模型)1()1()(221sTssTKsG)1()1(g2wsssK)(sR)(sC图3-17典型II型系统的结构T1T2(1/T1＜ωc＜1/T2)43dB/L0w1120cg21-1/sω4040图3-18典型II型系统开环对数频率特性090-1/sω180hKlg201由于分母中s2项对应的相频特性是–180°，为了把相频特性抬到–180°线以上，以保证系统稳定，应选择参数满足1/T1＜ωc＜1/T2。442.典型Ⅱ型系统参数和动态性能指标的关系典型II型系统开环传递函数中，系统的动态性能取决于K、T1和T2。与典型I型系统一样，时间常数T2是被调节对象的固有参数；系统的可调参数有K和T1，这两个参数确定后，系统的动态性能就可以完全确定了。由于有两个待定参数，故比典型I型系统的参数选择工作要复杂一些。45为分析问题方便引入新变量h，令1221TThdB/L0w1120cg21-1/sω4040图3-18典型II型系统开环对数频率特性090-1/sω180hKlg201h是斜率为-20dB/dec的中频段宽度(对数坐标)，称作“中频宽中频宽”。这是一个重要参数，中频段的状况对控制系统的动态品质起着决定性的作用。46c11c1lg20lg20lg40lg20Kc1K设ω=1处在-40dB/dec特性段，由图可以看出因此可以证明,当时,21cmax2222221121111111ThhhThTTTTK21c将代入上式中,有47用最大相位裕量求得的参数为22211ThhKhTT三阶最佳系统按h=4设计的系统既有一定的相对稳定性又有较快的响应,称为“三阶最佳系统”。2221814TKTT48•5.5.3两种系统比较典型I型系统和典型Ⅱ型系统除了在稳态误差上的区别以外，在动态性能中，•典型I型系统可以做到超调量小，但抗扰性能稍差，•典型Ⅱ型系统的超调量相对较大，抗扰性能却比较好。这是设计时选择典型系统的重要依据。49设计自动控制系统的一般方法设计自动控制系统的一般方法：：1）从调查研究、分析设计任务开始，根据系统提出的动、静态性能指标，以及经济性、可靠性要求，确定初步设计方案、选择元部件，拟定整个系统的电路原理图。2）根据自动控制系统的结构、各单元间的相互关系和参数，确定系统固有部分的数学模型。3）对系统固有部分进行相应的线性化处理和简化处理，从而得到系统固有部分的开环频率特性。5.6系统结构的近似处理和非典型系统的典型化504）根据性能指标确定系统的预期开环频率特性。所谓所谓预期开环频率特性就是满足系统性能指标的典型系统的预期开环频率特性就是满足系统性能指标的典型系统的开环对数幅频特性。开环对数幅频特性。5）工程上，为便于设计通常以系统固有部分的开环频工程上，为便于设计通常以系统固有部分的开环频率特性为基础，将系统校正成典型系统。其方法是：将率特性为基础，将系统校正成典型系统。其方法是：将系统的预期开环频率特性与固有部分的开环频率特性进系统的预期开环频率特性与固有部分的开环频率特性进行比较，得到校正装置的开环频率特性，并以此确定校行比较，得到校正装置的开环频率特性，并以此确定校正装置的结构与参数。这种校正方法称为预期频率特性正装置的结构与参数。这种校正方法称为预期频率特性校正法。校正法。6）通过实验或调试使系统全面达到性能指标的要求。51系统固有部分开环频率特性的确定系统固有部分开环频率特性的确定：：•系统固有部分开环频率特性的确定应根据系统的组成结构、各单元间的相互关系，建立系统的数学模型。•实际系统的固有部分往往是比较复杂的，将它们校正成典型系统后，会使校正装置的形式变得相当复杂，难以实现。因此，在校正前需对系统的固有部分进行适当的简化处理，包括对系统非线性元件进行合理的线性化处理和在对系统性能指标影响不大的前提下，对系统进行适当的简化处理。521.系统结构的近似处理1)1)小惯性环节群等效为一个惯性环节小惯性环节群等效为一个惯性环节)1)(1)(1()(321sssKsGggg1)(1321sggg•结论：当系统有多个小惯性环节时，在一定的条件下，可以将它们近似地看成是一个小惯性环节，其时间常数等于原系统各小时间常数之和。532)2)高阶系统的降阶处理高阶系统的降阶处理1)(2BsAsKsG当A＜＜B时,可以近似成一个大惯性环节1)(BsKsG543)3)低频段大惯性环节的近似处理低频段大惯性环节的近似处理设传递函数1)1)(1(1)(321ssssGggg当τg1＞＞τg2及τg1＞＞τg3时，大惯性环节近似成积分环节1)1(1)(321ssssGggg55•需要说明的是以上的这些近似处理一定需要说明的是以上的这些近似处理一定要满足一些近似条件的。要满足一些近似条件的。•近似处理虽可把问题简化近似处理虽可把问题简化,,但这必然会带但这必然会带来误差。来误差。562.非典型系统的典型化工程上，为便于设计通常以系统固有部分的开环频率工程上，为便于设计通常以系统固有部分的开环频率特性为基础，将系统校正成典型系统。其方法是：将特性为基础，将系统校正成典型系统。其方法是：将系统的预期开环频率特性与固有部分的开环频率特性系统的预期开环频率特性与固有部分的开环频率特性进行比较，得到校正装置的开环频率特性，并以此确进行比较，得到校正装置的开环频率特性，并以此确定校正装置的结构与参数。这种校正方法称为预期频定校正装置的结构与参数。这种校正方法称为预期频率特性校正法。率特性校正法。基本思路基本思路::先对系统固有部分作近似处理，然后再在系统中串入适当的调节器，使校正后的系统成为典型Ⅰ型系统或Ⅱ型系统。R(s)R(s)GGcc(s)(s)GG00(s)(s)C(s)C(s)校正装置校正装置固有系统固有系统57R(s)R(s)GGcc(s)(s)GG00(s)(s)C(s)C(s)校正装置校正装置固有系统固有系统校正成典型Ⅱ型系统后系统的开环传递函数为)1()1()()(2210sTssTKsGsGc)1()()(0TssKsGsGc校正成典型Ⅰ型系统后系统的开环传递函数为