《数列的概念及简单表示法》高二年级上册PPT课件（第2.1.1课时）.pptx

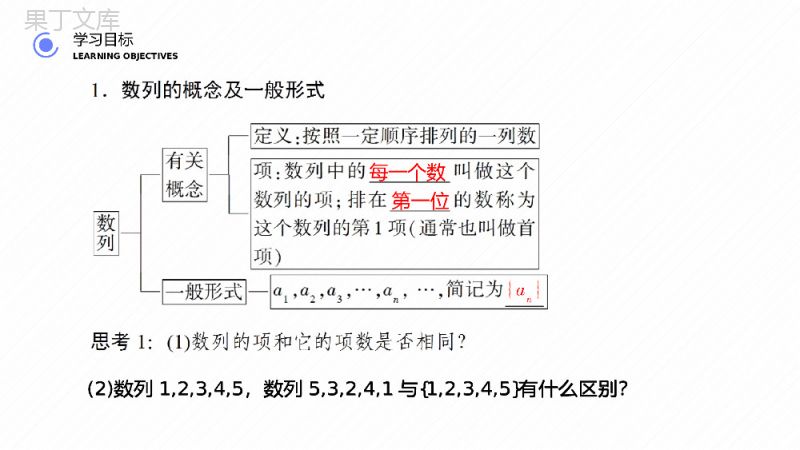
第二章数列主讲人：办公资源2.1.1第1课时数列的概念及简单表示法目录CONTENS学习目标LEARNINGOBJECTIVES011.理解数列的概念(重点).2.掌握数列的通项公式及应用(重点).3.能根据数列的前几项写出数列的一个通项公式(难点、易错点)．01学习目标LEARNINGOBJECTIVES学习目标LEARNINGOBJECTIVES每一个数第一位(2)数列1,2,3,4,5，数列5,3,2,4,1与{1,2,3,4,5}有什么区别？(2)数列1,2,3,4,5，数列5,3,2,4,1与{1,2,3,4,5}有什么区别？学习目标LEARNINGOBJECTIVES[提示](1)数列的项与它的项数是不同的概念．数列的项是指这个数列中的某一个确定的数，是一个函数值，也就是相当于f(n)，而项数是指这个数在数列中的位置序号，它是自变量的值，相当于f(n)中的n.(2)数列1,2,3,4,5和数列5,3,2,4,1为两个不同的数列，因为二者的元素顺序不同，而集合{1,2,3,4,5}与这两个数列也不相同，一方面形式上不一致，另一方面，集合中的元素具有无序性．[提示](1)数列的项与它的项数是不同的概念．数列的项是指这个数列中的某一个确定的数，是一个函数值，也就是相当于f(n)，而项数是指这个数在数列中的位置序号，它是自变量的值，相当于f(n)中的n.(2)数列1,2,3,4,5和数列5,3,2,4,1为两个不同的数列，因为二者的元素顺序不同，而集合{1,2,3,4,5}与这两个数列也不相同，一方面形式上不一致，另一方面，集合中的元素具有无序性．学习目标LEARNINGOBJECTIVES2．数列的分类类别含义按项的个数有穷数列项数的数列无穷数列项数的数列按项的变化趋势递增数列从第2项起，每一项都它的前一项的数列递减数列从第2项起，每一项都它的前一项的数列常数列各项的数列摆动数列从第2项起，有些项它的前一项，有些项小于它的前一项的数列有限无限大于小于相等大于2．数列的分类类别含义按项的个数有穷数列项数的数列无穷数列项数的数列按项的变化趋势递增数列从第2项起，每一项都它的前一项的数列递减数列从第2项起，每一项都它的前一项的数列常数列各项的数列摆动数列从第2项起，有些项它的前一项，有些项小于它的前一项的数列学习目标LEARNINGOBJECTIVES3.数列的通项公式如果数列{an}的第n项与之间的关系可以用一个式子来表示，那么这个公式叫做这个数列的通项公式．序号n3.数列的通项公式如果数列{an}的第n项与之间的关系可以用一个式子来表示，那么这个公式叫做这个数列的通项公式．学习目标LEARNINGOBJECTIVES4．数列与函数的关系从函数的观点看，数列可以看作是特殊的函数，关系如下表：定义域(或它的有限子集{1,2,3，…，n})解析式数列的通项公式值域自变量时对应的一列函数值构成表示方法(1)通项公式(解析法)；(2)；(3)思考：数列的通项公式an＝f(n)与函数解析式y＝f(x)有什么异同？正整数集N＋从小到大依次取值列表法图象法4．数列与函数的关系从函数的观点看，数列可以看作是特殊的函数，关系如下表：定义域(或它的有限子集{1,2,3，…，n})解析式数列的通项公式值域自变量时对应的一列函数值构成表示方法(1)通项公式(解析法)；(2)；(3)思考：数列的通项公式an＝f(n)与函数解析式y＝f(x)有什么异同？学习目标LEARNINGOBJECTIVES[提示]如图，数列可以看成以正整数集N(或它的有限子集{1,2，…，n})为定义域的函数，an＝f(n)当自变量按照从小到大的顺序依次取值时所对应的一列函数值．不同之处是定义域，数列中的n必须是从1开始且连续的正整数，函数的定义域可以是任意非空数集．[提示]如图，数列可以看成以正整数集N(或它的有限子集{1,2，…，n})为定义域的函数，an＝f(n)当自变量按照从小到大的顺序依次取值时所对应的一列函数值．不同之处是定义域，数列中的n必须是从1开始且连续的正整数，函数的定义域可以是任意非空数集．学习目标LEARNINGOBJECTIVES[基础自测]1．思考辨析(1)数列1,1,1，…是无穷数列．()(2)数列1,2,3,4和数列1,2,4,3是同一个数列．()(3)有些数列没有通项公式．()[答案](1)√(2)×(3)√[基础自测]1．思考辨析(1)数列1,1,1，…是无穷数列．()(2)数列1,2,3,4和数列1,2,4,3是同一个数列．()(3)有些数列没有通项公式．()[答案](1)√(2)×(3)√学习目标LEARNINGOBJECTIVES提示：(1)正确．每项都为1的常数列，有无穷多项．(2)错误．虽然都是由1,2,3,4四个数构成的数列，但是两个数列中后两个数顺序不同，不是同一个数列．(3)正确．某些数列的第n项an和n之间可以建立一个函数关系式，这个数列就有通项公式，否则，不能建立一个函数关系式，这个数列就没有通项公式．提示：(1)正确．每项都为1的常数列，有无穷多项．(2)错误．虽然都是由1,2,3,4四个数构成的数列，但是两个数列中后两个数顺序不同，不是同一个数列．(3)正确．某些数列的第n项an和n之间可以建立一个函数关系式，这个数列就有通项公式，否则，不能建立一个函数关系式，这个数列就没有通项公式．学习目标LEARNINGOBJECTIVES2．600是数列1×2,2×3,3×4,4×5，…的第________项．24[an＝n(n＋1)＝600＝24×25，所以n＝24.]3．数列{an}满足an＝log2(n2＋3)－2，则log23是这个数列的第________项.3[令an＝log2(n2＋3)－2＝log23，解得n＝3.]2．600是数列1×2,2×3,3×4,4×5，…的第________项．24[an＝n(n＋1)＝600＝24×25，所以n＝24.]3．数列{an}满足an＝log2(n2＋3)－2，则log23是这个数列的第________项.3[令an＝log2(n2＋3)－2＝log23，解得n＝3.]学习目标LEARNINGOBJECTIVES4．数列1,2,7，10，13，…中的第26项为________．219[因为a1＝1＝1，a2＝2＝4，a3＝7，a4＝10，a5＝13，所以an＝3n－2，所以a26＝3×26－2＝76＝219.]4．数列1,2,7，10，13，…中的第26项为________．219[因为a1＝1＝1，a2＝2＝4，a3＝7，a4＝10，a5＝13，所以an＝3n－2，所以a26＝3×26－2＝76＝219.]02合作探究COOPERATIVEINQUIRY合作探究COOPERATIVEINQUIRY数列的概念及分类例1、已知下列数列：①2011,2012,2013,2014,2015,2016；②1，12，14，…，12n－1，…；③1，－23，35，…，－1n－1·n2n－1，…；数列的概念及分类例1、已知下列数列：①2011,2012,2013,2014,2015,2016；②1，12，14，…，12n－1，…；③1，－23，35，…，－1n－1·n2n－1，…；合作探究COOPERATIVEINQUIRY④1,0，－1，…，sinnπ2，…；⑤2,4,8,16,32，…；⑥－1，－1，－1，－1.其中，有穷数列是________，无穷数列是________，递增数列是________，递减数列是________，常数列是________，摆动数列是________(填序号)．④1,0，－1，…，sinnπ2，…；⑤2,4,8,16,32，…；⑥－1，－1，－1，－1.其中，有穷数列是________，无穷数列是________，递增数列是________，递减数列是________，常数列是________，摆动数列是________(填序号)．合作探究COOPERATIVEINQUIRY①⑥②③④⑤①⑤②⑥③④[①为有穷数列且为递增数列；②为无穷、递减数列；③为无穷、摆动数列；④是摆动数列，是无穷数列，也是周期为4的周期数列；⑤为递增数列，也是无穷数列；⑥为有穷数列，也是常数列．]①⑥②③④⑤①⑤②⑥③④[①为有穷数列且为递增数列；②为无穷、递减数列；③为无穷、摆动数列；④是摆动数列，是无穷数列，也是周期为4的周期数列；⑤为递增数列，也是无穷数列；⑥为有穷数列，也是常数列．]合作探究COOPERATIVEINQUIRY[规律方法]1．与集合中元素的性质相比较，数列中的项的性质具有以下特点：(1)确定性：一个数是或不是某一数列中的项是确定的，集合中的元素也具有确定性；(2)可重复性：数列中的数可以重复，而集合中的元素不能重复出现(即互异性)；(3)有序性：一个数列不仅与构成数列的“数”有关，而且与这些数的排列顺序有关，而集合中的元素没有顺序(即无序性)；(4)数列中的每一项都是数，而集合中的元素还可以代表除数字外的其他事物．[规律方法]1．与集合中元素的性质相比较，数列中的项的性质具有以下特点：(1)确定性：一个数是或不是某一数列中的项是确定的，集合中的元素也具有确定性；(2)可重复性：数列中的数可以重复，而集合中的元素不能重复出现(即互异性)；(3)有序性：一个数列不仅与构成数列的“数”有关，而且与这些数的排列顺序有关，而集合中的元素没有顺序(即无序性)；(4)数列中的每一项都是数，而集合中的元素还可以代表除数字外的其他事物．合作探究COOPERATIVEINQUIRY2．判断数列是哪一种类型的数列时要紧扣概念及数列的特点．对于递增、递减、摆动还是常数列要从项的变化趋势来分析；而有穷还是无穷数列则看项的个数有限还是无限．2．判断数列是哪一种类型的数列时要紧扣概念及数列的特点．对于递增、递减、摆动还是常数列要从项的变化趋势来分析；而有穷还是无穷数列则看项的个数有限还是无限．合作探究COOPERATIVEINQUIRY[跟踪训练]1．给出下列数列：(1)2010～2017年某市普通高中生人数(单位：万人)构成数列82,93,105,118,132,147,163,180.(2)无穷多个3构成数列3，3，3，3，….(3)－2的1次幂，2次幂，3次幂，4次幂，…构成数列－2,4，－8,16，－32，….其中，有穷数列是________，无穷数列是________，递增数列是________，常数列是________，摆动数列是________.(1)(2)(3)(1)(2)(3)[(1)为有穷数列；(2)(3)是无穷数列，同时(1)也是递增数列；(2)为常数列；(3)为摆动数列．][跟踪训练]1．给出下列数列：(1)2010～2017年某市普通高中生人数(单位：万人)构成数列82,93,105,118,132,147,163,180.(2)无穷多个3构成数列3，3，3，3，….(3)－2的1次幂，2次幂，3次幂，4次幂，…构成数列－2,4，－8,16，－32，….其中，有穷数列是________，无穷数列是________，递增数列是________，常数列是________，摆动数列是________.(1)(2)(3)(1)(2)(3)[(1)为有穷数列；(2)(3)是无穷数列，同时(1)也是递增数列；(2)为常数列；(3)为摆动数列．]合作探究COOPERATIVEINQUIRY由数列的前几项求通项公式例2、写出数列的一个通项公式，使它的前4项是下列各数：(1)－1，12，－13，14；(2)3，3，15，21；(3)0.9,0.99,0.999,0.9999；(4)3,5,3,5.思路探究：①求数列的通项公式时，是否应考虑将个别项或各项进行适当的变形？②数列的通项公式唯一吗？由数列的前几项求通项公式例2、写出数列的一个通项公式，使它的前4项是下列各数：(1)－1，12，－13，14；(2)3，3，15，21；(3)0.9,0.99,0.999,0.9999；(4)3,5,3,5.思路探究：①求数列的通项公式时，是否应考虑将个别项或各项进行适当的变形？②数列的通项公式唯一吗？合作探究COOPERATIVEINQUIRY[解](1)任何一个整数都可以看成一个分数，所以此数列可以看做是自然数列的倒数，正负相间用(－1)的多少次幂进行调整，其一个通项公式为an＝(－1)n·1n.(2)数列可化为3，9，15，21，即3×1，3×3，3×5，3×7，…，每个根号里面可分解成两数之积，前一个因数为常数3，后一个因数为2n－1，故原数列的一个通项公式为an＝32n－1＝6n－3.[解](1)任何一个整数都可以看成一个分数，所以此数列可以看做是自然数列的倒数，正负相间用(－1)的多少次幂进行调整，其一个通项公式为an＝(－1)n·1n.(2)数列可化为3，9，15，21，即3×1，3×3，3×5，3×7，…，每个根号里面可分解成两数之积，前一个因数为常数3，后一个因数为2n－1，故原数列的一个通项公式为an＝32n－1＝6n－3.合作探究COOPERATIVEINQUIRY(3)原数列可变形为1－110，1－1102，1－1103，1－1104，…，故数列的一个通项公式为an＝1－110n.(4)数列给出前4项，其中奇数项为3，偶数项为5，所以通项公式的一种表示方法为an＝3n为奇数5n为偶数.此数列还可以这样考虑，3与5的算术平均数为3＋52＝4,4＋1＝5,4－1＝3，因此数列的一个通项公式又可以写为an＝4＋(－1)n.(3)原数列可变形为1－110，1－1102，1－1103，1－1104，…，故数列的一个通项公式为an＝1－110n.(4)数列给出前4项，其中奇数项为3，偶数项为5，所以通项公式的一种表示方法为an＝3n为奇数5n为偶数.此数列还可以这样考虑，3与5的算术平均数为3＋52＝4,4＋1＝5,4－1＝3，因此数列的一个通项公式又可以写为an＝4＋(－1)n.合作探究COOPERATIVEINQUIRY[规律方法]1．据所给数列的前几项求其通项公式时，需仔细观察分析，抓住以下几方面的特征：①分式中分子、分母的特征；②相邻项的变化特征；③拆项后的特征；④各项符号特征等，并对此进行归纳、联想．2．观察、分析数列中各项的特点是最重要的，观察出项与序号之间的关系、规律，利用我们熟知的一些基本数列(如自然数列、奇偶数列等)转换而使问题得到解决，对于正负符号变化，可用(－1)n或(－1)n＋1来调整．[规律方法]1．据所给数列的前几项求其通项公式时，需仔细观察分析，抓住以下几方面的特征：①分式中分子、分母的特征；②相邻项的变化特征；③拆项后的特征；④各项符号特征等，并对此进行归纳、联想．2．观察、分析数列中各项的特点是最重要的，观察出项与序号之间的关系、规律，利用我们熟知的一些基本数列(如自然数列、奇偶数列等)转换而使问题得到解决，对于正负符号变化，可用(－1)n或(－1)n＋1来调整．合作探究COOPERATIVEINQUIRY[跟踪训练]2．写出下列数列的一个通项公式：(1)0,3,8,15,24，…；(2)1，－3,5，－7,9，…；(3)112，223，334，445，…；(4)1,11,111,1111，….[跟踪训练]2．写出下列数列的一个通项公式：(1)0,3,8,15,24，…；(2)1，－3,5，－7,9，…；(3)112，223，334，445，…；(4)1,11,111,1111，….合作探究COOPERATIVEINQUIRY[解](1)观察数列中的数，可以看到0＝1－1,3＝4－1,8＝9－1,15＝16－1,24＝25－1，…，所以它的一个通项公式是an＝n2－1(n∈N)．(2)数列各项的绝对值为1,3,5,7,9，…，是连续的正奇数，并且数列的奇数项为正，偶数项为负，所以它的一个通项公式为an＝(－1)n＋1(2n－1)(n∈N)．[解](1)观察数列中的数，可以看到0＝1－1,3＝4－1,8＝9－1,15＝16－1,24＝25－1，…，所以它的一个通项公式是an＝n2－1(n∈N)．(2)数列各项的绝对值为1,3,5,7,9，…，是连续的正奇数，并且数列的奇数项为正，偶数项为负，所以它的一个通项公式为an＝(－1)n＋1(2n－1)(n∈N)．合作探究COOPERATIVEINQUIRY(3)此数列的整数部分1,2,3,4，…恰好是序号n，分数部分与序号n的关系为nn＋1，故所求的数列的一个通项公式为an＝n＋nn＋1＝n2＋2nn＋1(n∈N)．(4)原数列的各项可变为19×9，19×99，19×999，19×9999，…，易知数列9,99,999,9999，…的一个通项公式为an＝10n－1，所以原数列的一个通项公式为an＝19(10n－1)(n∈N)．(3)此数列的整数部分1,2,3,4，…恰好是序号n，分数部分与序号n的关系为nn＋1，故所求的数列的一个通项公式为an＝n＋nn＋1＝n2＋2nn＋1(n∈N)．(4)原数列的各项可变为19×9，19×99，19×999，19×9999，…，易知数列9,99,999,9999，…的一个通项公式为an＝10n－1，所以原数列的一个通项公式为an＝19(10n－1)(n∈N)．合作探究COOPERATIVEINQUIRY数列通项公式的应用[探究问题]1．数列12，34，78，1516，3132，…的通项公式是什么？该数列的第7项是什么？255256是否为该数列中的一项？为什么？提示：由数列各项的特点可归纳出其通项公式为an＝2n－12n，当n＝7时，a7＝27－127＝127128，若255256为该数列中的一项，则2n－12n＝255256，解得n＝8，所以255256是该数列中的第8项．数列通项公式的应用[探究问题]1．数列12，34，78，1516，3132，…的通项公式是什么？该数列的第7项是什么？255256是否为该数列中的一项？为什么？提示：由数列各项的特点可归纳出其通项公式为an＝2n－12n，当n＝7时，a7＝27－127＝127128，若255256为该数列中的一项，则2n－12n＝255256，解得n＝8，所以255256是该数列中的第8项．合作探究COOPERATIVEINQUIRY2．已知数列{an}的通项公式为an＝－n2＋2n＋1，该数列的图象有何特点？试利用图象说明该数列的单调性及所有的正数项．提示：由数列与函数的关系可知，数列{an}的图象是分布在二次函数y＝－x2＋2x＋1图象上的离散的点，如图所示，从图象上可以看出该数列是一个递减数列，且前两项为正数项，从第3项往后各项为负数项．2．已知数列{an}的通项公式为an＝－n2＋2n＋1，该数列的图象有何特点？试利用图象说明该数列的单调性及所有的正数项．提示：由数列与函数的关系可知，数列{an}的图象是分布在二次函数y＝－x2＋2x＋1图象上的离散的点，如图所示，从图象上可以看出该数列是一个递减数列，且前两项为正数项，从第3项往后各项为负数项．合作探究COOPERATIVEINQUIRY例3、已知数列{an}的通项公式为an＝3n2－28n.(1)写出此数列的第4项和第6项；(2)问－49是否是该数列的一项？如果是，应是哪一项？68是否是该数列的一项呢？思路探究：(1)将n＝4，n＝6分别代入an求出数值即可；(2)由3n2－28n＝－49和3n2－28n＝68，求得n是否为正整数判断．例3、已知数列{an}的通项公式为an＝3n2－28n.(1)写出此数列的第4项和第6项；(2)问－49是否是该数列的一项？如果是，应是哪一项？68是否是该数列的一项呢？思路探究：(1)将n＝4，n＝6分别代入an求出数值即可；(2)由3n2－28n＝－49和3n2－28n＝68，求得n是否为正整数判断．合作探究COOPERATIVEINQUIRY[解](1)a4＝3×42－28×4＝－64，a6＝3×62－28×6＝－60.(2)由3n2－28n＝－49解得n＝7或n＝73(舍去)，所以－49是该数列的第7项；由3n2－28n＝68解得n＝－2或n＝343，均不合题意，所以68不是该数列的项．[解](1)a4＝3×42－28×4＝－64，a6＝3×62－28×6＝－60.(2)由3n2－28n＝－49解得n＝7或n＝73(舍去)，所以－49是该数列的第7项；由3n2－28n＝68解得n＝－2或n＝343，均不合题意，所以68不是该数列的项．合作探究COOPERATIVEINQUIRY母题探究：1.(变结论)若本例中的条件不变，(1)试写出该数列的第3项和第8项；(2)问20是不是该数列的一项？若是，应是哪一项？[解](1)因为an＝3n2－28n，所以a3＝3×32－28×3＝－57，a8＝3×82－28×8＝－32.(2)令3n2－28n＝20，解得n＝10或n＝－23(舍去)，所以20是该数列的第10项．母题探究：1.(变结论)若本例中的条件不变，(1)试写出该数列的第3项和第8项；(2)问20是不是该数列的一项？若是，应是哪一项？[解](1)因为an＝3n2－28n，所以a3＝3×32－28×3＝－57，a8＝3×82－28×8＝－32.(2)令3n2－28n＝20，解得n＝10或n＝－23(舍去)，所以20是该数列的第10项．合作探究COOPERATIVEINQUIRY2．(变条件，变结论)若将例题中的“an＝3n2－28n”变为“an＝n2＋2n－5”，试判断数列{an}的单调性．[解]∵an＝n2＋2n－5，∴an＋1－an＝(n＋1)2＋2(n＋1)－5－(n2＋2n－5)＝n2＋2n＋1＋2n＋2－5－n2－2n＋5＝2n＋3.∵n∈N，∴2n＋3>0，∴an＋1>an.∴数列{an}是递增数列．2．(变条件，变结论)若将例题中的“an＝3n2－28n”变为“an＝n2＋2n－5”，试判断数列{an}的单调性．[解]∵an＝n2＋2n－5，∴an＋1－an＝(n＋1)2＋2(n＋1)－5－(n2＋2n－5)＝n2＋2n＋1＋2n＋2－5－n2－2n＋5＝2n＋3.∵n∈N，∴2n＋3>0，∴an＋1>an.∴数列{an}是递增数列．合作探究COOPERATIVEINQUIRY[规律方法]1．由通项公式写出数列的指定项，主要是对n进行取值，然后代入通项公式，相当于函数中，已知函数解析式和自变量的值求函数值．2．判断一个数是否为该数列中的项，其方法是可由通项公式等于这个数求方程的根，根据方程有无正整数根便可确定这个数是否为数列中的项．3．在用函数的有关知识解决数列问题时，要注意它的定义域是N(或它的有限子集{1,2,3，…，n})这一约束条件．[规律方法]1．由通项公式写出数列的指定项，主要是对n进行取值，然后代入通项公式，相当于函数中，已知函数解析式和自变量的值求函数值．2．判断一个数是否为该数列中的项，其方法是可由通项公式等于这个数求方程的根，根据方程有无正整数根便可确定这个数是否为数列中的项．3．在用函数的有关知识解决数列问题时，要注意它的定义域是N(或它的有限子集{1,2,3，…，n})这一约束条件．03当堂达标REACHINGTHEGOALINCOURT当堂达标REACHINGTHEGOALINCOURT1．下列说法正确的是()A．数列1,3,5,7，…，2n－1可以表示为1,3,5,7，…B．数列1,0，－1，－2与数列－2，－1,0,1是相同的数列C．数列n＋1n的第k项为1＋1kD．数列0,2,4,6,8，…可记为{2n}【答案】C1．下列说法正确的是()A．数列1,3,5,7，…，2n－1可以表示为1,3,5,7，…B．数列1,0，－1，－2与数列－2，－1,0,1是相同的数列C．数列n＋1n的第k项为1＋1kD．数列0,2,4,6,8，…可记为{2n}【答案】C当堂达标REACHINGTHEGOALINCOURT2．（2019年上高县校级月考）在数列1,1,2,3,5,8，x,21,34,55中，x等于()A．11B．12C．13D．14【答案】C[观察可知该数列从第3项开始每一项都等于它前面相邻两项的和，故x＝5＋8＝13.]2．（2019年上高县校级月考）在数列1,1,2,3,5,8，x,21,34,55中，x等于()A．11B．12C．13D．14【答案】C[观察可知该数列从第3项开始每一项都等于它前面相邻两项的和，故x＝5＋8＝13.]当堂达标REACHINGTHEGOALINCOURT3．（2019年厦门模拟）已知数列2，10，4，…，23n－1，…，则8是该数列的第________项．【答案】11[令23n－1＝8，得n＝11.]4．（2019年重庆模拟）若数列{an}的通项公式是an＝3－2n，则a2n＝________，a2a3＝________.【答案】3－4n15[根据通项公式我们可以求出这个数列的任意一项．因为an＝3－2n，所以a2n＝3－22n＝3－4n，a2a3＝3－223－23＝15.]3．（2019年厦门模拟）已知数列2，10，4，…，23n－1，…，则8是该数列的第________项．【答案】11[令23n－1＝8，得n＝11.]4．（2019年重庆模拟）若数列{an}的通项公式是an＝3－2n，则a2n＝________，a2a3＝________.【答案】3－4n15[根据通项公式我们可以求出这个数列的任意一项．因为an＝3－2n，所以a2n＝3－22n＝3－4n，a2a3＝3－223－23＝15.]感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明当堂达标REACHINGTHEGOALINCOURT5．（2019年徐汇区校级月考）已知数列9n2－9n＋29n2－1.(1)求这个数列的第10项；(2)98101是不是该数列中的项，为什么？(3)求证：数列中的各项都在区间(0,1)内．【答案】设f(n)＝9n2－9n＋29n2－1＝3n－13n－23n－13n＋1＝3n－23n＋1.(1)令n＝10，得第10项a10＝f(10)＝2831.(2)令3n－23n＋1＝98101，得9n＝300.此方程无正整数解，所以98101不是该数列中的项．(3)证明：∵an＝3n－23n＋1＝3n＋1－33n＋1＝1－33n＋1，又n∈N，∴0<33n＋1<1，∴0