《匀变速直线运动的常用推论》人教版高一物理必修1PPT课件.pptx

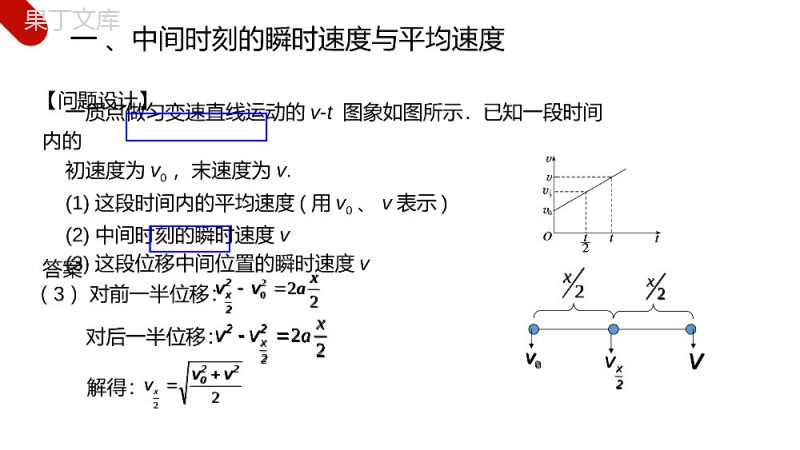
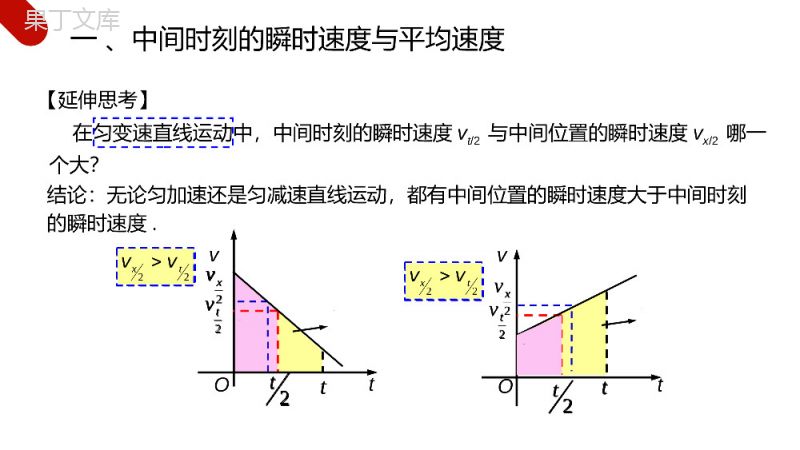
讲解人：办公资源时间：2020.5.20MENTALHEALTHCOUNSELINGPPT第5节匀变速直线运动的常用推论第二章匀变速直线运动的研究人教版高中物理必修1答案【问题设计】一质点做匀变速直线运动的v-t图象如图所示．已知一段时间内的初速度为v0，末速度为v.(1)这段时间内的平均速度(用v0、v表示)(2)中间时刻的瞬时速度(3)这段位移中间位置的瞬时速度（1）v-t图像与t轴所围面积表示位移tx20vv位移：平均速度：20vvvtx(2)由图中可知：中间时刻的瞬时速度大小等于梯形中位线长度202vvvt位移/时间2tv2xv一、中间时刻的瞬时速度与平均速度tx20vv20vvvtx202vvvt2tv2xv答案【问题设计】一质点做匀变速直线运动的v-t图象如图所示．已知一段时间内的初速度为v0，末速度为v.(1)这段时间内的平均速度(用v0、v表示)(2)中间时刻的瞬时速度v(3)这段位移中间位置的瞬时速度v（3）对前一半位移：对后一半位移：22220vvvx解得：2220xavv22x22xa22x2v-v0vv2xv2x2x一、中间时刻的瞬时速度与平均速度22220vvvx2220xavv22x22xa22x2v-v0vv2xv2x2x【要点提炼】1．中间时刻的瞬时速度2．中间位置的瞬时速度3．平均速度公式总结：，适用条件：．，适用条件：．，适用条件：．注意对匀变速直线运动有20vv22220vvvxtxv2vvv02tvv202vvvvt任意运动匀变速直线运动匀变速直线运动2tv一、中间时刻的瞬时速度与平均速度20vv22220vvvxtxv2vvv02tvv202vvvvt2tv【延伸思考】在匀变速直线运动中，中间时刻的瞬时速度vt/2与中间位置的瞬时速度vx/2哪一个大？tOv2tv2ttOv2tttxx/22tv22txvv结论：无论匀加速还是匀减速直线运动，都有中间位置的瞬时速度大于中间时刻的瞬时速度.2xv2xv一、中间时刻的瞬时速度与平均速度2tv2t2ttt22txvv2tv22txvv2xv2xv证明【问题设计】物体做匀变速直线运动，加速度为a，从某时刻起T时间内的位移为x1，紧接着第二个T时间内的位移为x2.试证明：x2-x1＝aT2.设物体的初速度为v0自计时起T时间内的位移x1=v0T＋aT2/2①在第2个T时间内的位移x2=v0·2T＋a(2T)2/2－x1=v0T＋3aT2/2②由①②两式得连续相等时间内的位移差为Δx=x2-x1=v0T+3aT2/2-v0T-aT2/2=aT2即Δx=aT2.二.重要推论Δx=aT2的推导及应用1．匀变速直线运动中，在连续相等的时间T内的位移之差为一恒定值，即Δx=_________.2．应用(1)判断物体是否做匀变速直线运动如果Δx=x2-x1=x3-x2=……=xn-xn-1=aT2成立，则a为一恒量，说明物体做匀变速直线运动．(2)求加速度利用连续相等时间段内的位移差Δx，可求得a=Δx/T2.aT2【要点提炼】二.重要推论Δx=aT2的推导及应用建立时间坐标轴，把初速度为零的匀变速直线运动按时间T等分，如下图所示：初速度为零的匀加速直线运动的速度公式：可得：已知：所以：TTTTTTT1v2v3v7v4v5v6v00vatvtvnttttn::3:2:1::::321nvvvvn::3:2:1::::3211.1T秒末，2T秒末，…….瞬时速度之比:三.初速度为零的匀变速直线运动的比例式1v2v3v7v4v5v6v00vatvtvnttttn::3:2:1::::321nvvvvn::3:2:1::::321建立时间坐标轴，把初速度为零的匀变速直线运动按时间T等分，如下图所示：初速度为零的匀加速直线运动的位移公式：可得：已知：所以：TTTTTTT00v1s2s3s4s221atx2txnttttn::3:2:1::::3212222321::3:2:1::::nsxxxn2.1T内，2T内，3T内，…的位移之比三.初速度为零的匀变速直线运动的比例式00v1s2s3s4s221atx2txnttttn::3:2:1::::3212222321::3:2:1::::nsxxxn建立时间坐标轴，把初速度为零的匀变速直线运动按时间T等分，如下图所示：由图可得：已知：可得：TTTTTTT00v1s2s3s4s1x2x3x4x11sx122ssx233ssx1nnnssx2222321::3:2:1::::nssssn)12(::5:3:1)1(::)23(:)12(:1::::2222222321nnnxxxxn3.第一个T内,第二个T内,第三个T内…的位移比:三.初速度为零的匀变速直线运动的比例式00v1s2s3s4s1x2x3x4x11sx122ssx233ssx1nnnssx2222321::3:2:1::::nssssn)12(::5:3:1)1(::)23(:)12(:1::::2222222321nnnxxxxn建立位移坐标轴，把初速度为零的匀变速直线运动按位移s等分，如下图所示：初速度为零的匀加速直线运动的时间公式：可得：所以：sssssss00v1t2t3t4taxt2ast21ast222ast323anstn2nttttn::3:2:1::::3214.前1个s,前2个s，前3个s，…所用时间的比值:三.初速度为零的匀变速直线运动的比例式00v1t2t3t4taxt2ast21ast222ast323anstn2nttttn::3:2:1::::321建立位移坐标轴，把初速度为零的匀变速直线运动按位移s等分，如下图所示：由图可得：已知：所以：sssssss00v1t2t3t4t1T2T3T4T11tT122ttT233ttT1nnnttTnttttn::3:2:1::::3211::23:12:1::::321nnTTTTn5.通过第1个s，通过第2个s，通过第3个s…所用时间的比值:三.初速度为零的匀变速直线运动的比例式00v1t2t3t4t1T2T3T4T11tT122ttT233ttT1nnnttTnttttn::3:2:1::::3211::23:12:1::::321nnTTTTn建立位移坐标轴，把初速度为零的匀变速直线运动按位移s等分，如下图所示：初速度为零的匀加速直线运动的位移速度关系式：可得：所以：sssssss00v1v2v3v4v5vaxv2sav21sav222sav323nsavn2nvvvvn::3:2:1::::3216.第1个s末，第2个s末，第3个s末…的速度之比:三.初速度为零的匀变速直线运动的比例式00v1v2v3v4v5vaxv2sav21sav222sav323nsavn2nvvvvn::3:2:1::::321【例1】：A、B、C三点在同一条直线上，一物体从A点由静止开始做匀加速直线运动，经过B点的速度是v，到C点的速度是3v，则xAB∶xBC等于()A．18∶B．16∶C．15∶D．13∶解析Aaxvv220222(3)2BCaxvv202ABaxv81BCABxx速度—位移公式从A到B：从B到C：初速度为0典型例题axvv220222(3)2BCaxvv202ABaxv81BCABxx例2：一质点做匀变速直线运动，初速度v0＝2m/s,4s内位移为20m，求：(1)质点4s末的速度(2)质点2s末的速度解析解法一：利用平均速度公式5224v4s末速度m/s84v220m/s5m/s4vv2s末的速度x=20m2402vvvtxvm/s84v典型例题5224vm/s84v220m/s5m/s4vv2402vvvtxvm/s84v解析例2：一质点做匀变速直线运动，初速度v0＝2m/s,4s内位移为20m，求：(1)质点4s末的速度(2)质点2s末的速度解法二：利用两个基本公式2021attxv21.5m/sa由解得：at0vv4(21.54)m8m/sv由解得：2(21.52)m5m/sv4s末的速度2s末的速度x=20mv0=2m/sv2=?v4=?t/s典型例题2021attxv21.5m/saat0vv4(21.54)m8m/sv2(21.52)m5m/sv解析例3.一辆汽车从静止开始由甲地出发，沿平直公路开往乙地，汽车先做匀加速直线运动，接着做匀减速直线运动，开到乙地刚好停止，其速度—时间图象如图所示，那么0～t和t～3t两段时间内()A．加速度大小之比为31∶B．位移大小之比为12∶C．平均速度大小之比为21∶D．平均速度大小之比为11∶BDv-t图中面积：表示位移v-t图中斜率：表示加速度12:2:1aa2:1:21xx1:120:20:21vvvv典型例题12:2:1aa2:1:21xx1:120:20:21vvvv解析解法一：利用关系式Δx=aT22aTx2222m/s2m/s44880Txa前4s内的位移：2020422144821vvattxm/s80v例4：做匀加速直线运动的物体，从开始计时起连续两个4s的时间间隔内通过的位移分别是48m和80m，则这个物体的初速度和加速度各是多少？典型例题2aTx2222m/s2m/s44880Txa2020422144821vvattxm/s80v解析例5．汽车自O点出发从静止开始在平直公路上做匀加速直线运动，途中在6s内分别经过P、Q两根电线杆，已知P、Q电线杆相距60m，车经过电线杆Q时的速率是15m/s，则下列说法正确的是()A．经过P杆时的速率是5m/sB．车的加速度是1.5m/s2C．P、O间的距离是7.5mD．车从出发到经过Q所用的时间是9sACD2156602PQPtxvvvm/s5Pv221555m/sm/s63QPatvv22502m7.5m523POPOPaxxv15s9s53QOQOQattv从P到Q:从O到P:从O到Q:OPQ典型例题2156602PQPtxvvvm/s5Pv221555m/sm/s63QPatvv22502m7.5m523POPOPaxxv15s9s53QOQOQattv例6．(2019·兰州一中高一检测)汽车刹车后做匀减速直线运动，经3s后停止运动，那么，在这连续的三个1s内汽车通过的位移之比为()A．1∶3∶5B．5∶3∶1C．1∶2∶3D．3∶2∶1【解析】用逆向思维可以把汽车刹车的运动认为是初速度为零的匀加速直线运动的逆过程，所以这连续的三个1s内汽车通过的位移之比为5∶3∶1，B项对．B典型例题例6．(2019·兰州一中高一检测)汽车刹车后做匀减速直线运动，经3s后停止运动，那么，在这连续的三个1s内汽车通过的位移之比为()A．1∶3∶5B．5∶3∶1C．1∶2∶3D．3∶2∶1【解析】用逆向思维可以把汽车刹车的运动认为是初速度为零的匀加速直线运动的逆过程，所以这连续的三个1s内汽车通过的位移之比为5∶3∶1，B项对．讲解人：办公资源时间：2020.5.20MENTALHEALTHCOUNSELINGPPT感谢你的聆听第二章匀变速直线运动的研究人教版高中物理必须1感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明