《平面向量数量积的物理背景及其含义》高一年级下册PPT课件.pptx

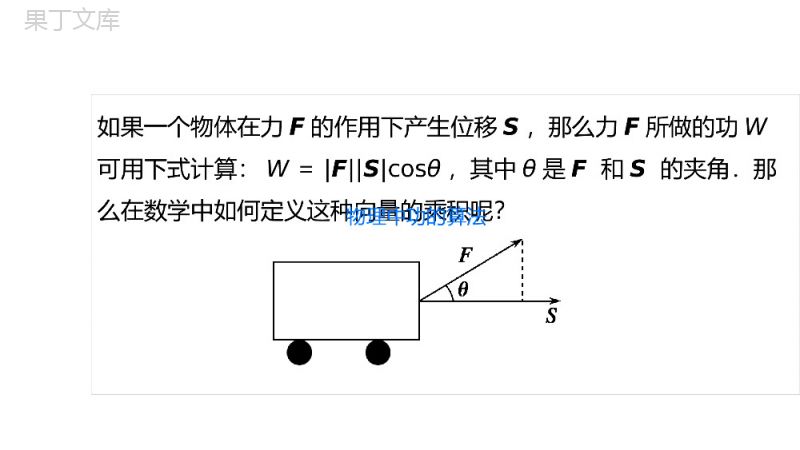
平面向量的数量积第二章平面向量2.4.1平面向量数量积的物理背景及其含义CONTENT01自主预习学案栏目导航02互动探究学案03课时作业学案01自主预习学案第二章平面向量如果一个物体在力F的作用下产生位移S，那么力F所做的功W可用下式计算：W＝FScosθ，其中θ是F和S的夹角．那么在数学中如何定义这种向量的乘积呢？物理中功的算法1．平面向量的数量积的定义定义已知两个非零向量a与b，我们把数量_____________叫做a与b的数量积(或内积)，其中θ是a与b的夹角记法记作a·b，即a·b＝abcosθabcosθ1．平面向量的数量积的定义定义已知两个非零向量a与b，我们把数量_____________叫做a与b的数量积(或内积)，其中θ是a与b的夹角记法记作a·b，即a·b＝abcosθabcosθ第二章平面向量[知识点拨]规定：零向量与任一向量的数量积为零．关于平面向量数量积的说明：(1)“·”是数量积的运算符号，既不能省略不写，也不能写成“×”；(2)数量积的结果为数量，不再是向量；(3)向量数量积的正负由两个向量的夹角θ决定：当θ是锐角时，数量积为正；当θ是钝角时，数量积为负；当θ是直角时，数量积等于零．第二章平面向量2．(1)投影的概念①向量b在a的方向上的投影为__________.②向量a在b的方向上的投影为__________.(2)数量积的几何意义．数量积a·b等于a的长度a与_____________________________________________________的乘积．bcosθacosθb在a的方向上的投影bcosθbcosθacosθb在a的方向上的投影bcosθ第二章平面向量[知识点拨]关于投影的说明：(1)向量a在向量b方向上的投影与向量b在向量a方向上的投影是不同的；(2)向量a在向量b方向上的投影acosθ＝a·bb；向量b在向量a方向上的投影bcosθ＝a·ba.[知识点拨]关于投影的说明：(1)向量a在向量b方向上的投影与向量b在向量a方向上的投影是不同的；(2)向量a在向量b方向上的投影acosθ＝a·bb；向量b在向量a方向上的投影bcosθ＝a·ba.第二章平面向量3．平面向量数量积的性质设a，b是两个非零向量，则由向量数量积的定义，有：(1)a⊥b⇔______________.(2)当a与b同向时，a·b＝________________；当a与b反向时，a·b＝__________________.特别地，a·a＝a2＝a2或a＝a·a.(3)a·b≤________________，当且仅当向量a，b共线，即a∥b时，等号成立．(4)cosθ＝a·bab，其中θ是非零向量a与b的夹角．a·b＝0ab－abab3．平面向量数量积的性质设a，b是两个非零向量，则由向量数量积的定义，有：(1)a⊥b⇔______________.(2)当a与b同向时，a·b＝________________；当a与b反向时，a·b＝__________________.特别地，a·a＝a2＝a2或a＝a·a.(3)a·b≤________________，当且仅当向量a，b共线，即a∥b时，等号成立．(4)cosθ＝a·bab，其中θ是非零向量a与b的夹角．第二章平面向量[知识点拨]数量积的性质及其应用性质(1)可用于解决与两个非零向量垂直有关的问题；性质(2)表明：当两个向量相等时，这两个向量的数量积等于向量长度的平方，因此可用于求向量的模；性质(3)可以解决有关“向量不等式”的问题；性质(4)的实质是平面向量数量积的逆用，可用于求两向量的夹角，也称为夹角公式．第二章平面向量4．平面向量数量积的运算律由于数量积是完全不同于数与向量乘法的一种运算，这种运算涉及长度、角度，因此有如下三条运算律：已知向量a，b，c和实数λ，则(1)交换律：__________________；(2)数乘结合律：__________________________；(3)分配律：_____________________.a·b＝b·a(λa)·b＝λ(a·b)＝a·(λb)(a＋b)·c＝a·c＋b·c第二章平面向量[知识点拨]1.在实数运算中，若ab＝0，则a与b中至少有一个为0.但是在向量数量积的运算中，不能由a·b＝0推出a＝0或b＝0.事实上，当a≠0时，由a·b＝0不能推出b一定是零向量，这是因为对任一与a垂直的非零向量b，都有a·b＝0.实际上，由a·b＝0可推出以下四种结论：(1)a＝0，b＝0；(2)a＝0，b≠0；(3)a≠0，b＝0；(4)a≠0，b≠0，但a⊥b.2．已知实数a，b，c(b≠0)，则ab＝bc⇒a＝c.但对向量的数量积，该推理不正确，即a·b＝b·c⇒/a＝c.[知识点拨]1.在实数运算中，若ab＝0，则a与b中至少有一个为0.但是在向量数量积的运算中，不能由a·b＝0推出a＝0或b＝0.事实上，当a≠0时，由a·b＝0不能推出b一定是零向量，这是因为对任一与a垂直的非零向量b，都有a·b＝0.实际上，由a·b＝0可推出以下四种结论：(1)a＝0，b＝0；(2)a＝0，b≠0；(3)a≠0，b＝0；(4)a≠0，b≠0，但a⊥b.2．已知实数a，b，c(b≠0)，则ab＝bc⇒a＝c.但对向量的数量积，该推理不正确，即a·b＝b·c⇒/a＝c.1．判断下列说法是否正确，正确的在后面的括号内打“√”，错误的打“×”．(1)0·a＝0a.()(2)若a·b＝0，则a与b至少有一个为零向量．()(3)若a·b>0，则a与b的夹角为锐角．()(4)若a·c＝b·c(c≠0)，则a＝b.()(5)对于任意向量a，都有a·a＝a2.()(6)一个向量在另一个向量方向上的投影是一个向量．()××××√×第二章平面向量2．若a＝3，b＝4，a，b的夹角为135°，则a·b＝()A．－32B．－62C．62D．12B[解析]∵a·b＝abcos135°＝3×4×(－22)＝－62.2．若a＝3，b＝4，a，b的夹角为135°，则a·b＝()A．－32B．－62C．62D．12[解析]∵a·b＝abcos135°＝3×4×(－22)＝－62.02互动探究学案第二章平面向量已知a＝2，b＝3，a与b的夹角为120°，试求：(1)a·b；(2)(a＋b)·(a－b)；(3)(2a－b)·(a＋3b)．[思路分析]根据数量积、模、夹角的定义，逐一进行计算即可．命题方向1平面向量的数量积⇨典例1第二章平面向量[解析](1)a·b＝abcos120°＝2×3×(－12)＝－3.(2)(a＋b)·(a－b)＝a2－a·b＋a·b－b2＝a2－b2＝a2－b2＝4－9＝－5.(3)(2a－b)·(a＋3b)＝2a2＋6a·b－a·b－3b2＝2a2＋5a·b－3b2＝2×4－5×3－3×9＝－34.[解析](1)a·b＝abcos120°＝2×3×(－12)＝－3.(2)(a＋b)·(a－b)＝a2－a·b＋a·b－b2＝a2－b2＝a2－b2＝4－9＝－5.(3)(2a－b)·(a＋3b)＝2a2＋6a·b－a·b－3b2＝2a2＋5a·b－3b2＝2×4－5×3－3×9＝－34.第二章平面向量『规律总结』求向量的数量积的两个关键点求向量的数量积时，需明确两个关键点：相关向量的模和夹角．若相关向量是两个或两个以上向量的线性运算，则需先利用向量数量积的运算律及多项式乘法的相关公式进行化简．第二章平面向量〔跟踪练习1〕已知a＝4，b＝5，当(1)a∥b；(2)a⊥b；(3)a与b的夹角为60°时，分别求a与b的数量积．[解析](1)∵a∥b，若a与b同向，则θ＝0°，∴a·b＝abcos0°＝4×5＝20；若a与b反向，则θ＝180°，∴a·b＝abcos180°＝4×5×(－1)＝－20.(2)当a⊥b时，θ＝90°，∴a·b＝abcos90°＝0.(3)当a与b夹角为60°时，a·b＝abcos60°＝4×5×12＝10.[解析](1)∵a∥b，若a与b同向，则θ＝0°，∴a·b＝abcos0°＝4×5＝20；若a与b反向，则θ＝180°，∴a·b＝abcos180°＝4×5×(－1)＝－20.(2)当a⊥b时，θ＝90°，∴a·b＝abcos90°＝0.(3)当a与b夹角为60°时，a·b＝abcos60°＝4×5×12＝10.第二章平面向量命题方向2向量的投影⇨典例2如图所示，在△ABC中，AB＝AC＝4，∠BAC＝90°，D是边BC的中点，求：(1)AB→在BD→方向上的投影；(2)BD→在AB→方向上的投影．[思路分析]首先结合图形求出AB→与BD→的夹角，然后利用定义求解投影．如图所示，在△ABC中，AB＝AC＝4，∠BAC＝90°，D是边BC的中点，求：(1)AB→在BD→方向上的投影；(2)BD→在AB→方向上的投影．[思路分析]首先结合图形求出AB→与BD→的夹角，然后利用定义求解投影．第二章平面向量[解析]如图所示，连接AD，因为AB＝AC＝4，∠BAC＝90°，所以△ABC是等腰直角三角形．又D是BC边的中点，所以AD⊥BC，∠ABD＝45°，所以BD＝22.延长AB到E，则AB→与BD→的夹角为∠DBE＝180°－45°＝135°.(1)AB→在BD→方向上的投影是AB→cos135°＝4×(－22)＝－22.(2)BD→在AB→方向上的投影是BD→cos135°＝22×(－22)＝－2.[解析]如图所示，连接AD，因为AB＝AC＝4，∠BAC＝90°，所以△ABC是等腰直角三角形．又D是BC边的中点，所以AD⊥BC，∠ABD＝45°，所以BD＝22.延长AB到E，则AB→与BD→的夹角为∠DBE＝180°－45°＝135°.(1)AB→在BD→方向上的投影是AB→cos135°＝4×(－22)＝－22.(2)BD→在AB→方向上的投影是BD→cos135°＝22×(－22)＝－2.第二章平面向量『规律总结』注意区分a在b方向上投影的数量acosa，b与b在a方向上的投影的数量bcosb，a两者之间的差异．第二章平面向量命题方向3利用向量的数量积解决有关模、夹角问题⇨典例3(1)已知a＝b＝5，向量a、b夹角θ＝π3，求a＋b；(2)已知a，b是两个非零向量，且a＝b＝a－b，求a与a＋b的夹角．[思路分析](1)先求a·b，再用a＋b与a·b的联系求解．(2)根据题中所给等式求出向量a与a＋b的夹角公式中涉及的所有量，代入公式求解即可．(1)已知a＝b＝5，向量a、b夹角θ＝π3，求a＋b；(2)已知a，b是两个非零向量，且a＝b＝a－b，求a与a＋b的夹角．[思路分析](1)先求a·b，再用a＋b与a·b的联系求解．(2)根据题中所给等式求出向量a与a＋b的夹角公式中涉及的所有量，代入公式求解即可．第二章平面向量[解析](1)a·b＝abcosθ＝5×5×cosπ3＝252.a＋b＝a＋b2＝a2＋2a·b＋b2＝25＋2×252＋25＝53.(2)∵a＝a－b，∴a2＝a－b2＝a2－2a·b＋b2.又a＝b，∴a·b＝12a2，[解析](1)a·b＝abcosθ＝5×5×cosπ3＝252.a＋b＝a＋b2＝a2＋2a·b＋b2＝25＋2×252＋25＝53.(2)∵a＝a－b，∴a2＝a－b2＝a2－2a·b＋b2.又a＝b，∴a·b＝12a2，第二章平面向量又a＋b＝a＋b2＝a2＋2a·b＋b2＝3a，设a与a＋b的夹角为θ，则cosθ＝a·a＋baa＋b＝a2＋a·baa＋b＝a2＋12a2a·3a＝32，又θ∈[0，π]，∴θ＝π6，即a与a＋b的夹角为π6.又a＋b＝a＋b2＝a2＋2a·b＋b2＝3a，设a与a＋b的夹角为θ，则cosθ＝a·a＋baa＋b＝a2＋a·baa＋b＝a2＋12a2a·3a＝32，又θ∈[0，π]，∴θ＝π6，即a与a＋b的夹角为π6.第二章平面向量『规律总结』1.利用数量积求解长度问题是数量积的重要应用，要掌握此类问题的处理方法：(1)a＝a·a＝a2或a＝a·a.(2)a±b＝a±b2＝a2＋b2±2a·b.2．向量夹角公式cos〈a，b〉＝a·bab的计算中涉及了向量运算和数量运算，计算时要区别进行的是向量运算还是数量运算．从而保证计算结果准确无误．『规律总结』1.利用数量积求解长度问题是数量积的重要应用，要掌握此类问题的处理方法：(1)a＝a·a＝a2或a＝a·a.(2)a±b＝a±b2＝a2＋b2±2a·b.2．向量夹角公式cos〈a，b〉＝a·bab的计算中涉及了向量运算和数量运算，计算时要区别进行的是向量运算还是数量运算．从而保证计算结果准确无误．利用向量的数量积判断几何图形的形状典例4在△ABC中，AB→＝c，BC→＝a，CA→＝b，且a·b＝b·c＝c·a，试判断△ABC的形状．[思路分析]易知a＋b＋c＝0，分别将a、b、c移至等号右边，得到三个等式，分别平方可得a·b、b·c、c·a，选取两个等式相减即可得到a、b、c中两个向量的长度之间的关系．在△ABC中，AB→＝c，BC→＝a，CA→＝b，且a·b＝b·c＝c·a，试判断△ABC的形状．[思路分析]易知a＋b＋c＝0，分别将a、b、c移至等号右边，得到三个等式，分别平方可得a·b、b·c、c·a，选取两个等式相减即可得到a、b、c中两个向量的长度之间的关系．第二章平面向量[解析]在△ABC中，易知AB→＋BC→＋CA→＝0，即a＋b＋c＝0，因此a＋c＝－b，a＋b＝－c，从而a＋b2＝－c2，a＋c2＝－b2，两式相减可得b2＋2a·b－c2－2a·c＝c2－b2，则2b2＋2(a·b－a·c)＝2c2，因为a·b＝c·a＝a·c，所以2b2＝2c2，即b＝c.同理可得a＝b，故AB→＝BC→＝CA→，即△ABC是等边三角形．[解析]在△ABC中，易知AB→＋BC→＋CA→＝0，即a＋b＋c＝0，因此a＋c＝－b，a＋b＝－c，从而a＋b2＝－c2，a＋c2＝－b2，两式相减可得b2＋2a·b－c2－2a·c＝c2－b2，则2b2＋2(a·b－a·c)＝2c2，因为a·b＝c·a＝a·c，所以2b2＝2c2，即b＝c.同理可得a＝b，故AB→＝BC→＝CA→，即△ABC是等边三角形．第二章平面向量『规律总结』依据向量数量积的有关知识判断平面图形的形状，关键是由已知条件建立数量积、向量的长度、向量的夹角等之间关系，移项、两边平方是常用手段，这样可以出现数量积及向量的长度等信息，为说明边相等、边垂直指明方向．已知a＝2，b＝3，a与b的夹角为120°，求a＋b及a－b的值．混淆向量的模与实数的运算典例5[错解]由题意，得a·b＝abcos120°＝－3.∴a＋b＝a2＋2a·b＋b2＝22＋2×?－3?＋32＝7.∴a－b＝a2－b2a＋b＝57＝577.[错解]由题意，得a·b＝abcos120°＝－3.∴a＋b＝a2＋2a·b＋b2＝22＋2×?－3?＋32＝7.∴a－b＝a2－b2a＋b＝57＝577.第二章平面向量[错因分析]该解法错误地类比实数运算中的法则，实际上a2－b2＝(a＋b)·(a－b)≤a＋ba－b.[思路分析]直接利用完全平方和(差)公式．[正解]由题意，得a·b＝abcos120°＝－3.∴a＋b＝a2＋2a·b＋b2＝22＋2×－3＋32＝7，a－b＝a2－2a·b＋b2＝22－2×－3＋32＝19.[正解]由题意，得a·b＝abcos120°＝－3.∴a＋b＝a2＋2a·b＋b2＝22＋2×－3＋32＝7，a－b＝a2－2a·b＋b2＝22－2×－3＋32＝19.第二章平面向量[误区警示]利用数量积求解模的问题，是数量积的重要应用，解决此类问题的方法是对向量进行平方，即利用公式：a·a＝a2，从而达到将向量转化为实数的目的．1．若a·c＝b·c(c≠0)，则()A．a＝bB．a≠bC．a＝bD．a在c方向上的投影与b在c方向上的投影必相等[解析]设a与c的夹角为θ1，b与c的夹角为θ2，∵a·c＝b·c，∴accosθ1＝bccosθ2，即acosθ1＝bcosθ2，故选D．D第二章平面向量2．下列命题正确的是()A．a·b＝abB．a·b≠0⇔a＋b≠0C．a·b＝0⇔ab＝0D．(a＋b)·c＝a·c＋b·c[解析]选项D是分配律，正确，A、B、C不正确．D感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明03课时作业学案第二章平面向量谢谢观看新课标导学数学必修④·人教A版