专题09-导数压轴题之拉格朗日中值定理详述版(解析版)

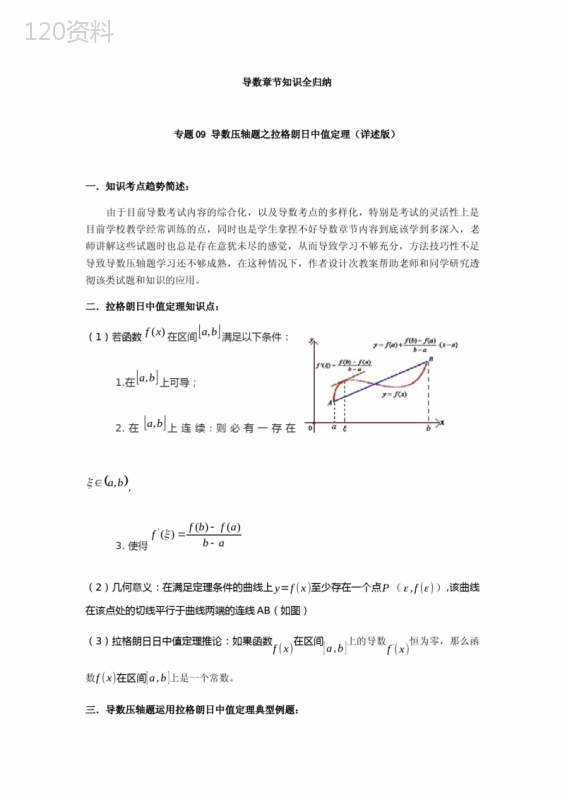
("导数章节知识全归纳专题09导数压轴题之拉格朗日中值定理（详述版）一．知识考点趋势简述：由于目前导数考试内容的综合化，以及导数考点的多样化，特别是考试的灵活性上是目前学校教学经常训练的点，同时也是学生拿捏不好导数章节内容到底该学到多深入，老师讲解这些试题时也总是存在意犹未尽的感觉，从而导致学习不够充分，方法技巧性不足导致导数压轴题学习还不够成熟，在这种情况下，作者设计次教案帮助老师和同学研究透彻该类试题和知识的应用。二．拉格朗日中值定理知识点：（1）若函数)(xf在区间\uf05b\uf05dba,满足以下条件：1.在\uf05b\uf05dba,上可导；2.在\uf05b\uf05dba,上连续:则必有一存在\uf028\uf029ba,\uf0ce\uf078,3.使得abafbff\uf02d\uf02d\uf03d)()()('\uf078（2）几何意义：在满足定理条件的曲线上y=f(x)至少存在一个点P（ε,f(ε)）,该曲线在该点处的切线平行于曲线两端的连线AB（如图）（3）拉格朗日日中值定理推论：如果函数f(x)在区间[a,b]上的导数f∙(x)恒为零，那么函数f(x)在区间[a,b]上是一个常数。三．导数压轴题运用拉格朗日中值定理典型例题：例：1.已知函数(aR)．（1）讨论函数的单调性；（2）若，为函数的两个极值点，证明：．解：【分析】（1）求出导函数，根据的解的情况分类讨论得单调性；（2）由（1）知，化简，不等式化为，再由不妨设，转化为只要证这个不等式可利用（1）中的结论证明（也可利用拉格朗日中值定理进行求解）即：存在x°使得f,(x°)=f(x1)−f(x2)x1−x2>2-4a．【详解】（1），令当即时，，在上单调递增；当即或时，①当时，在上单调递增；②当时，令，+0-0+递增极大值递减极小值递增综上：当时，在上单调递增；当时，在上单调递增，在上单调递减.（2）由（1）知时有两个极值点，且，不妨设，要证即证，即，设由（1）知当时，在上单调递增，，则在上单调递减，.原式得证.【点睛】关键点点睛：本题考查用导数研究函数的单调性，证明不等式．含有参数的函数在求单调区间时一般需要分类讨论，可根据的根的情况分类讨论．对于双变量的不等式的证明需要进行变形，利用双变量之间的关系，转化为只有一个变量的不等式，从而可引入新函数，利用函数的性质进行证明．解题过程中换元法是一种重要的方法．例：2.已知函数.1,ln)1(21)(2\uf03e\uf02d\uf02b\uf02d\uf03daxaaxxxf（1）讨论函数)(xf的单调性；（2）证明:若5\uf03ca,则对任意\uf028\uf029\uf02b\uf0a5\uf0ce,0,21xx,21xx\uf0b9,有1)()(2121\uf02d\uf03e\uf02d\uf02dxxxfxf.【解析】：（1）\uf028\uf029\uf02b\uf0a5\uf0ce,0x,xaxxxf)1)(1()('\uf02d\uf02b\uf02d\uf03d,取决于分子)1)(1(axx\uf02d\uf02b\uf02d,开口向上的抛物线,两根为:1,1\uf02da;讨论两根的大小.i.若2\uf03da,两根相等:11\uf03d\uf02da,\uf028\uf029\uf02b\uf0a5\uf0ce,0x单调递增;ii.若12\uf03e\uf03ea,11\uf03c\uf02da,\uf028\uf0291,1\uf02da单调递减,\uf028\uf029\uf028\uf029\uf02b\uf0a5\uf02d,1,1,0a单调递增;iii.若2\uf03ea,11\uf03e\uf02da,\uf028\uf0291,1\uf02da单调递减,\uf028\uf029\uf028\uf029\uf02b\uf0a5\uf02d,1,1,0a单调递增;（2）法一:设21xx\uf03e,只需证:1221)()(xxxfxf\uf02d\uf03e\uf02d,即2211)()(xxfxxf\uf02b\uf03e\uf02b,构造函数xxaaxxxxfxg\uf02b\uf02d\uf02b\uf02d\uf03d\uf02b\uf03dln)1(21)()(2,只需证明)(xg在\uf028\uf029\uf02b\uf0a5,0上单调递增，)1(121)1()('\uf02d\uf02d\uf02d\uf0d7\uf0b3\uf02d\uf02b\uf02d\uf02d\uf03daxaxxaaxxg2)11(1\uf02d\uf02d\uf02d\uf03da,51\uf03c\uf03ca\uf051,0)('\uf03e\uf05cxg,即)(xg在\uf028\uf029\uf02b\uf0a5,0单调递增,当021\uf03e\uf03exx时,0)()(21\uf03e\uf02dxgxg,即0)()(2121\uf03e\uf02d\uf02b\uf02dxxxfxf,1)()(2121\uf02d\uf03e\uf02d\uf02dxxxfxf,同理当210xx\uf03c\uf03c时,1)()(2121\uf02d\uf03e\uf02d\uf02dxxxfxf.法二:由拉格朗日中值中定值可知存在\uf078,使)()()('2121\uf078fxxxfxf\uf03d\uf02d\uf02d,\uf028\uf029\uf02b\uf0a5\uf0ce,0\uf078,xaaxxf1)('\uf02d\uf02b\uf02d\uf03daa\uf02d\uf02d\uf0b312,设ta\uf03d\uf02d1,\uf028\uf0292,0\uf0cet,则112122\uf02d\uf03e\uf02d\uf02b\uf02d\uf03d\uf02d\uf02dttaa,即1)()(2121\uf02d\uf03e\uf02d\uf02dxxxfxf.例：3.已知函数（1）若，求函数的单调区间；（2）设，若对任意，恒有，求a的取值范围.解：【分析】（1）借助题设条件运用导数和单调性的关系分类求解；（2）借助题设条件构造函数运用导数的知识推证.【详解】解：（1）当时，由已知得，所以，令得，即时，；时，；故单调递增区间为，单调递减区间为；（2），由得，所以在单调递减，设从而对任意，恒有，即，令，则等价于在单调递减，即恒成立，从而恒成立，故设，则，当时，为减函数，时，，为增函数.∴,∴a的取值范围为.【点晴】方法点睛：导数是研究函数的单调性和极值最值问题的重要而有效的工具．本题就是以含参数的函数解析式为背景，考查的是导数知识在研究函数单调性和极值等方面的综合运用和分析问题解决问题的能力．本题的第一问求解时借助导数与函数单调性的关系，运用分类整合的数学思想分类求出其单调区间和单调性；第二问的求解中则先构造函数，然后再对函数求导，运用导数的知识研究函数的单调性，然后运用函数的单调性，从而使得问题简捷巧妙获证变式：1.已知函数.（1）讨论函数的单调性；（2）若存在两个极值点，求证：.解：【分析】（1）求出导函数，根据二次函数的与的关系来分类讨论函数的单调性，并注意一元二次方程根的正负与定义域的关系；（2）由是两个极值点得到对应的韦达定理形式，然后利用条件将转变为关于函数，再运用的关系将不等式转化为证，构造函数，分析函数的单调性，得出最值，不等式可得证.【详解】（1）解：函数的定义域为，，则.①当时，对，所以函数在上单调递增；②当时，，所以对，所以函数在上单调递增；③当时，令，得或，所以函数在，上单调递增；令，得，所以在上单调递减.（2）证明：由（1）知且，所以.又由.又因为所以要证，只需证.因为，所以只需证，即证.令，则，所以函数在上单调递增，所以对.所以.所以若存在两个极值点，则.【点睛】本题考查函数与导数的综合应用，属于较难题.导数中通过双极值点求解最值或证明不等式时，可通过双极值点对应的等式将待求的式子或待证明的式子转变为关于同一变量（注意变量的范围）的式子，然后通过构造新函数，分析新函数的单调性后从而达到求解最值或证明不等式的目的.变式：2.已知函数（为自然对数的底数），其中.（1）在区间上，是否存在最小值？若存在，求出最小值；若不存在，请说明理由.（2）若函数的两个极值点为，证明：.解：【分析】（1）对函数求导，令，得两根，从而得出的单调区间.由用作差法比较与的大小，结合，可知，则在区间单调递减，则其取得最小值；（2）由的韦达定理，得，则可消去a，得，.通过两边取对数，得和，将其代入需证不等式.再得，采用换元法，反证法，将所求不等式转化为.再用换元法，令构造函数，利用导函数求其最值，则可证明不等式.【详解】.解：（1）由条件可函数在上有意义，，令，得，，因为，所以，.所以当时，，当上，所以在上是增函数，在是减函数.由可知，当时，，当时，，当时，，因为，所以，又函数在上是减函数，且，所以函数在区间上的有最小值，其最小值为.（2）由（1）可知，当时函数存在两个极值点，且是方程的两根，所以，且，，，所以，，所以，又，由（1）可知，设，，则，故要证成立，只要证成立，下面证明不等式成立，构造函数，则，所以在上单调递增，，即成立，令，即得不等式，从而成立.【点睛】本题考查了利用导函数求函数的最值，证明不等式，其中换元法、反证法的应用是本题的关键，考查了转化的思想，属于综合性较强的难题.变式：3.已知函数.1ln)1()(2\uf02b\uf02b\uf02b\uf03daxxaxf（1）讨论函数)(xf的单调性；（2）设1\uf02d\uf03ca,如果对任意\uf028\uf029\uf02b\uf0a5\uf0ce,0,21xx,21214)()(xxxfxf\uf02d\uf0b3\uf02d,求a的取值范围.【解析】：（1）\uf028\uf029\uf02b\uf0a5\uf0ce,0x,xaaxxf12)(2'\uf02b\uf02b\uf03d,i.当0\uf0b3a时,0)('\uf03exf,)(xf在\uf028\uf029\uf02b\uf0a5\uf0ce,0x单调递增;ii.当1\uf02d\uf0a3a时,0)('\uf03cxf,)(xf在\uf028\uf029\uf02b\uf0a5\uf0ce,0x单调递减;iii.当01\uf03c\uf03c\uf02da时,由0)('\uf03dxf得aax21\uf02b\uf02d\uf03d,)(xf在\uf0f7\uf0f7\uf0f8\uf0f6\uf0e7\uf0e7\uf0e8\uf0e6\uf02b\uf02d\uf0ceaax21,0单调递增,在\uf0f7\uf0f7\uf0f8\uf0f6\uf0e7\uf0e7\uf0e8\uf0e6\uf02b\uf0a5\uf02b\uf02d\uf0ce,21aax单调递减.（2）法一:不妨设21xx\uf0b3,而当1\uf02d\uf03ca时,由（1）可知)(xf在\uf028\uf029\uf02b\uf0a5\uf0ce,0x单调递减,从而\uf028\uf029\uf02b\uf0a5\uf0ce\uf022,0,21xx,21214)()(xxxfxf\uf02d\uf0b3\uf02d等价于\uf028\uf029\uf02b\uf0a5\uf0ce\uf022,0,21xx,11224)(4)(xxfxxf\uf02b\uf0b3\uf02b.构造函数xxfxg4)()(\uf02b\uf03d,只需)(xg在\uf028\uf029\uf02b\uf0a5\uf0ce,0x单调递减,即0421)('\uf0a3\uf02b\uf02b\uf02b\uf03daxxaxg在\uf028\uf029\uf02b\uf0a5\uf0ce,0x恒成立,分离变量法:212)12(1214222\uf02d\uf02b\uf02d\uf03d\uf02b\uf02d\uf02d\uf0a3xxxxa,只需2)212)12((min22\uf02d\uf03d\uf02d\uf02b\uf02d\uf0a3xxa.法二:由拉格朗日定理知,21214)()(xxxfxf\uf02d\uf0b3\uf02d,等价于4)()(2121\uf0b3\uf02d\uf02dxxxfxf,在\uf028\uf029\uf02b\uf0a5,0存在\uf078,使得)()()('2121\uf078fxxxfxf\uf03d\uf02d\uf02d成立,只需4)('\uf0b3\uf078f恒成立,只需4)1(2212)(min'\uf0b3\uf02b\uf03d\uf02b\uf02b\uf03daaxaaxxf,得2,022\uf02d\uf0a3\uf0b3\uf02d\uf02baaa或1\uf0b3a(舍去).变式：4.已知函数f（x）x+alnx．（1）求f（x）在（1，f（1））处的切线方程（用含a的式子表示）（2）讨论f（x）的单调性；（3）若f（x）存在两个极值点x1，x2，证明：．解：【分析】（1）求出切点坐标，根据导函数求出切线斜率，即可得到切线方程；（2）求出导函数，对g（x）＝﹣x2+ax1﹣，进行分类讨论即可得到原函数单调性；（3）结合（2）将问题转为证明1，根据韦达定理转化为考虑h（x）＝2lnx﹣x的单调性比较大小即可得证.【详解】（1）∵f（x）x+alnx（x＞0）∴f′（x）（x＞0）∴当x＝1时，f（1）＝0，f′（1）＝﹣2+a，设切线方程为y＝（﹣2+a）x+b，代入（1，0），得b＝2﹣a，∴f（x）在（1，f（1））处的切线方程为y＝（﹣2+a）x+2﹣a．（2）函数的定义域为（0，+∞），函数的导数f′（x），设g（x）＝﹣x2+ax1﹣，注意到g（0）＝﹣1，①当a≤0时，g（x）＜0恒成立，即f′（x）＜0恒成立，此时函数f（x）在（0，+∞）上是减函数；②当a＞0时，判别式△＝a24﹣，（i）当0＜a≤2时，△≤0，即g（x）≤0，即f′（x）≤0恒成立，此时函数f（x）在（0，+∞）上是减函数；（ii）当a＞2时，令f′（x）＞0，得：x；令f′（x）＜0，得：0＜x或x；∴当a＞2时，f（x）在区间（，）单调递增，在（0，），（，+∞）单调递减；综上所述，综上当a≤2时，f（x）在（0，+∞）上是减函数，当a＞2时，在（0，），（，+∞）上是减函数，在区间（，）上是增函数．（3）由（2）知a＞2，0＜x1＜1＜x2，x1x2＝1，则f（x1）﹣f（x2）x1+alnx1[﹣x2+alnx2]＝（x2﹣x1）（1）+a（lnx1﹣lnx2）＝2（x2﹣x1）+a（lnx1﹣lnx2），则2，则问题转为证明1即可，即证明lnx1﹣lnx2＞x1﹣x2，则lnx1﹣lnx1，即lnx1+lnx1＞x1，即证2lnx1＞x1在（0，1）上恒成立，设h（x）＝2lnx﹣x，（0＜x＜1），其中h（1）＝0，求导得h′（x）10，则h（x）在（0，1）上单调递减，∴h（x）＞h（1），即2lnx﹣x0，故2lnx＞x，则a2﹣成立．【点睛】此题考查导函数的应用，根据几何意义求切线斜率，讨论函数的单调性，证明不等式，解决双变量问题，综合性强.",)