等边三角形第2课时(30度直角三角形)-八年级数学上册同步教材配套精品教学课件(人教版)

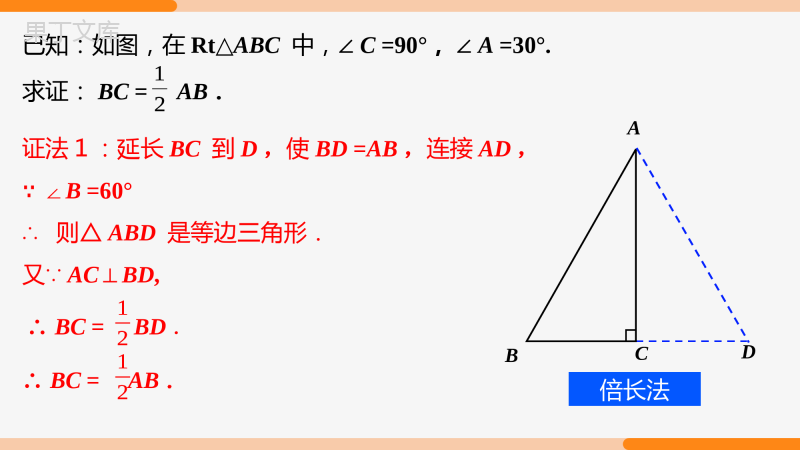
第十三章轴对称30°角的直角三角形的性质13.3.2等边三角形13.3.2等边三角形第2课时【学习目标】【学习目标】等腰三角形的判定探索含30°角的直角三角形的性质．会运用含30°角的直角三角形的性质进行有关的证明和计算．复习旧知回顾：等边三角形的性质和判定.元素等边三角形的性质等边三角形判定边角三线对称轴三线合一三个角都相等，且都是60º对称轴（3条）三条边都相等三条边相等三个角相等有一个角是60°的等腰三角形新知探究探究：观察下图三角板，回答下列问题(1)三角板各角分别多少度？(2)两个三角板摆成了一个什么三角形？说理由？(3)猜想最短直角边与斜边之间的数量关系？猜想：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.证法1：延长BC到D，使BD=AB，连接AD，∵∠B=60°∴则△ABD是等边三角形．又∵AC⊥BD,已知：如图，在Rt△ABC中，∠C=90°，∠A=30°.求证：BC=AB．21ABC∴BC=AB．12∴BC=BD．12D倍长法211212证明：在BA上截取BE=BC，连接EC.∵∠B=90°-∠A=60°，BE=BC，∴△BCE是等边三角形，∴∠BEC=60°，BE=EC=BC.∵∠A=30°，∴∠ECA=∠BEC－∠A=60°－30°=30°.∴AE=EC=BE=BC，∴AB=AE+BE=2BC.已知：如图，在Rt△ABC中，∠C=90°，∠A=30°.求证：BC=AB．21截半法EABC∴BC=AB．122112含30°角的直角三角形的性质在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.归纳知识在Rt△ABC中，∵∠C=90°，∠A=30°，∴BC=AB．12ABC12情景引入思考：如图，在△ABC中,(1)若AB=AC，则△ABC按边来分是什么三角形？(2)若AB=AC=BC，则△ABC是等腰三角形吗？还是什么三角形？(3)猜想等边三角形有那些性质？ABC元素边角三线对称轴等边三角形ABC探究新知ABCABC等腰三角形AB=AC∠B=∠C等边三角形AB=AC=BC∠A=∠B=∠C=60°思考：类比等腰三角形的性质，探究等边三角形的性质(1)等边三角形的三个内角之间有什么关系？思考：类比等腰三角形的性质，探究等边三角形的性质(2)等边三角形的“三线”有什么关系？有几条对称轴？？ABC结论每条边上的中线、高和所对角的平分线都“三线合一”.三条对称轴ABC三线合一顶角的平分线、底边的高、底边的中线一条对称轴等腰三角形等边三角形针对练习1.如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，CD是斜边AB上的高，AD＝3cm，则AB的长度是()A．3cmB．6cmC．9cmD．12cmD2.如图是屋架设计图的一部分，立柱BC垂直于横梁AD，AB＝8m，∠A＝30°，则立柱BC的长度为()A．4mB．8mC．10mD．16mA典例讲解例1.如图，在△ABC中,AB=AC，∠BAC=120°,D是BC的中点，DE⊥AB于E点，求证：BE=3EA.证明∵AB=AC，∠BAC=120°，∴∠B=∠C=30°.∵D是BC的中点，∴AD⊥BC.∴∠ADB=90°∠BAD=∠DAC=60°.∴AB=2AD.∵DE⊥AB，∴∠AED=90°，∴∠ADE=30°，∴AD=2AE.∴AB=4AE，∴BE=3AE.例2.如图，等腰三角形的底角为15°,腰长为20.求腰上的高.ACBD15°15°20解:过C作CD⊥BA,交BA的延长线于点D.∵∠B=∠ACB=15°(已知),∴∠DAC=∠B+∠ACB=15°+15°=30°，))∴CD=AC=×20=10.1212变式.等腰三角形的底角为15°,腰长为20.求这个三角形面积.1212课堂小结直角三角形性质角角与边等边三角形推导30°所对的直角边等于斜边的一半.边两锐角互余有一个角是直角勾股定理课堂练习1.如图，一棵树在一次强台风中于离地面3米处折断倒下，倒下部分与地面成30°角，这棵树在折断前的高度为()A．6米B．9米C．12米D．15米2.某市在旧城改造中，计划在一块如图所示的△ABC空地上种植草皮以美化环境，已知∠A＝150°，这种草皮每平方米售价a元，则购买这种草皮至少需要()A．300a元B．150a元C．450a元D．225a元BB3.如图是某商场一楼与二楼之间的手扶电梯示意图，其中AB、CD分别表示一楼、二楼地面的水平线，∠ABC＝150°，BC的长是8m，则乘电梯从点B到点C上升的高度h是()A．3mB．4mC．5mD．6mB4.如图，Rt△ABC中，∠C=90°，∠A=30°，AB+BC=12cm，则AB=________.ACB8cm5.如图，在△ABC中，∠C=90°，∠B=15°，DE是AB的垂直平分线，BE=5，则求AC的长．解连接AE，∵DE是AB的垂直平分线，∴BE=AE，∴∠EAB=∠B=15°，∴∠AEC=∠EAB+∠B=30°．∵∠C=90°，∴AC=AE=BE=2.5．1212DACEB12126.如图，某货轮于上午8时20分从A处出发，此时观测到海岛B的方位为北偏东60°，该货轮以每小时30海里的速度向东航行到C处，此时观测到海岛B的方位为北偏东30°，继续向东航行到D处，观测到海岛B的方位为北偏西30°.当货轮到达C处时恰好与海岛B相距60海里，求该货轮到达C，D处的时间．解：由已知，得∠BAC＝90°－60°＝30°，∠ACB＝90°＋30°＝120°，∠BCD＝∠BDC＝60°，∴∠ABC＝∠BCD－∠BAC＝30°，∠CBD＝180°－∠BCD－∠BDC＝60°，∴∠ABC＝∠BAC＝30°，∴AC＝BC＝60海里，∴货轮从A处到C处所需时间为60÷30＝2(小时)．∵∠CBD＝∠BCD＝∠BDC＝60°，∴△BCD是等边三角形，∴CD＝BC＝60海里，∴货轮从C处到D处所需时间为60÷30＝2(小时)，∴货轮从A处到D处所需时间为2＋2＝4(小时)．答：该货轮到达C处的时间是上午10时20分，到达D处的时间是中午12时20分．