湘教版数学九年级上册-《正切》习题课件5

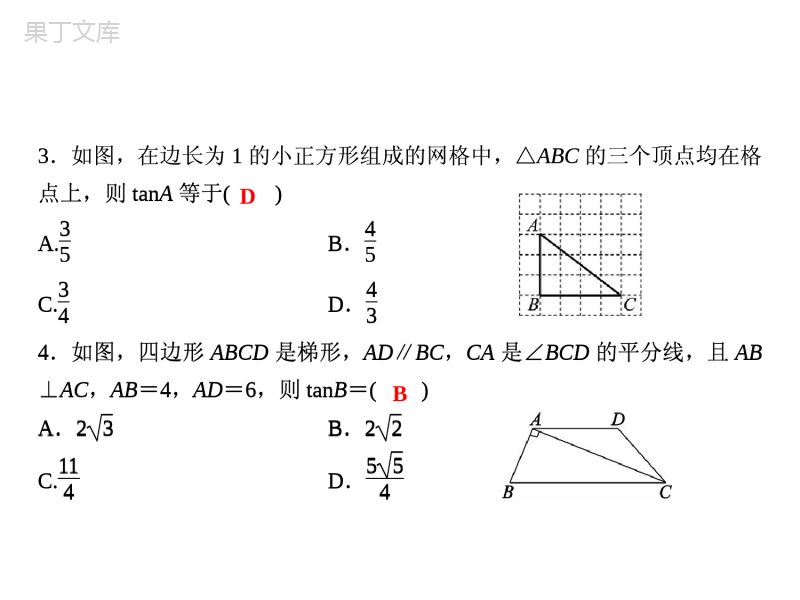
第4章锐角三角函数4．2正切1．在直角三角形中，锐角α的与的比叫作角α的正切，记作tanα，即tanα＝.2．对于锐角α的每一个确定的值，sinα有唯一确定的值与它对应，所以是的函数，同样地，cosα、tanα也是，我们把锐角α的正弦、余弦和正切统称为α的.对边邻边∠α的对边∠α的邻边sinαα的三角函数α的三角函数锐角三角函数1．在直角三角形中，锐角α的与的比叫作角α的正切，记作tanα，即tanα＝.2．对于锐角α的每一个确定的值，sinα有唯一确定的值与它对应，所以是的函数，同样地，cosα、tanα也是，我们把锐角α的正弦、余弦和正切统称为α的.∠α的对边∠α的邻边正切的定义1．在Rt△ABC中，∠C＝90°，tanA＝13，AC＝6，则BC的长为()A．6B．5C．4D．22．在Rt△ABC中，∠C＝90°，若斜边AB是直角边BC的3倍，则tanB的值是()A.13B．3C.24D．22DD正切的定义1．在Rt△ABC中，∠C＝90°，tanA＝13，AC＝6，则BC的长为()A．6B．5C．4D．22．在Rt△ABC中，∠C＝90°，若斜边AB是直角边BC的3倍，则tanB的值是()A.13B．3C.24D．223．如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tanA等于()A.35B．45C.34D．434．如图，四边形ABCD是梯形，AD∥BC，CA是∠BCD的平分线，且AB⊥AC，AB＝4，AD＝6，则tanB＝()A．23B．22C.114D．554DB3．如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tanA等于()A.35B．45C.34D．434．如图，四边形ABCD是梯形，AD∥BC，CA是∠BCD的平分线，且AB⊥AC，AB＝4，AD＝6，则tanB＝()A．23B．22C.114D．5545．如图所示，在Rt△ABC中，∠C＝90°，AB＝10，sinA＝35，求tanA和tanB的值．解：tanA＝34，tanB＝435．如图所示，在Rt△ABC中，∠C＝90°，AB＝10，sinA＝35，求tanA和tanB的值．解：tanA＝34，tanB＝43特殊角的三角函数值6．3tan30°的值等于()A.3B．33C.33D．327．计算sin245°＋cos30°·tan60°，其结果是()A．2B．1C.52D．548．在Rt△ABC中，∠C＝90°，∠B＝45°，则sinA＝，tanA＝.AA221特殊角的三角函数值6．3tan30°的值等于()A.3B．33C.33D．327．计算sin245°＋cos30°·tan60°，其结果是()A．2B．1C.52D．548．在Rt△ABC中，∠C＝90°，∠B＝45°，则sinA＝，tanA＝.2219．求下列各式的值：(1)sin60°tan30°－2cos230°tan45°；解：原式＝32×33－2×(32)2×1＝－1；(2)tan60°－tan45°3tan30°＋tan45°＋2sin30°tan30°.解：原式＝3－13＋1＋3＝2.9．求下列各式的值：(1)sin60°tan30°－2cos230°tan45°；解：原式＝32×33－2×(32)2×1＝－1；(2)tan60°－tan45°3tan30°＋tan45°＋2sin30°tan30°.解：原式＝3－13＋1＋3＝2.用计算器求锐角的正切值或已知正切值求锐角10．填空(精确到0.0001)：(1)cos42°≈；(2)cos80°25′≈.11．填空(精确到0.1°)：(1)若cosα＝0.3245，则α≈；(2)若cosα＝0.8434，则α≈.12．用计算器求值：(1)tan17°42′(精确到0.0001)；(2)已知tanβ≈0.32，求β的值(精确到0.1°)．0.74310.166571.1°32.5°解：(1)0.3191(2)17.7°用计算器求锐角的正切值或已知正切值求锐角10．填空(精确到0.0001)：(1)cos42°≈；(2)cos80°25′≈.11．填空(精确到0.1°)：(1)若cosα＝0.3245，则α≈；(2)若cosα＝0.8434，则α≈.12．用计算器求值：(1)tan17°42′(精确到0.0001)；(2)已知tanβ≈0.32，求β的值(精确到0.1°)．解：(1)0.3191(2)17.7°1．如图，在网格中，小正方形的边长均为1，点A、B、C都在格点上，则∠ABC的正切值是()A．2B．255C.55D．122．在△ABC中，若角A、B满足cosA－32＋(1－tanB)2＝0，则∠C的大小是()A．45°B．60°C．75°D．105°DD1．如图，在网格中，小正方形的边长均为1，点A、B、C都在格点上，则∠ABC的正切值是()A．2B．255C.55D．122．在△ABC中，若角A、B满足cosA－32＋(1－tanB)2＝0，则∠C的大小是()A．45°B．60°C．75°D．105°3．在△ABC中，AB＝AC＝3cm，BC＝2cm，则tanA2的值是()A.24B．22C.32D．244．式子2cos30°－tan45°－1－tan60°2的值是()A．23－2B．0C．23D．2DB3．在△ABC中，AB＝AC＝3cm，BC＝2cm，则tanA2的值是()A.24B．22C.32D．244．式子2cos30°－tan45°－1－tan60°2的值是()A．23－2B．0C．23D．25．在Rt△ABC中，∠C＝90°，AC＝4，tanB＝712，则BC＝.6．在Rt△ABC中，∠C＝90°，c＝8，b＝6，则最小角的正切值为.7．如果方程x2－4x＋3＝0的两个根分别是Rt△ABC的两条边，△ABC最小的内角为∠A，那么tanA的值为或.4877313245．在Rt△ABC中，∠C＝90°，AC＝4，tanB＝712，则BC＝.6．在Rt△ABC中，∠C＝90°，c＝8，b＝6，则最小角的正切值为.7．如果方程x2－4x＋3＝0的两个根分别是Rt△ABC的两条边，△ABC最小的内角为∠A，那么tanA的值为或.4877313248．如图，在Rt△ABC中，∠C＝90°，tanB＝34，求sinB、cosB的值．解：在Rt△ABC中，∵tanB＝ACBC＝34，∴设AC＝3k，BC＝4k.由勾股定理得：AB＝AC2＋BC2＝3k2＋4k2＝5k.∴sinB＝ACAB＝35，cosB＝BCAB＝45.8．如图，在Rt△ABC中，∠C＝90°，tanB＝34，求sinB、cosB的值．解：在Rt△ABC中，∵tanB＝ACBC＝34，∴设AC＝3k，BC＝4k.由勾股定理得：AB＝AC2＋BC2＝3k2＋4k2＝5k.∴sinB＝ACAB＝35，cosB＝BCAB＝45.9．在Rt△ABC中，∠C＝90°，D为BC中点，DE⊥AB于E，且tanB＝12，AE＝6，求DE的长．解：设DE＝x，∵∠C＝90°，tanB＝12，∴BE＝2x.∴由勾股定理得BD＝5x.∴BC＝25x.又∵tanB＝12，∴AC＝5x.∴由勾股定理得AB＝5x.∴AE＝5x－2x＝3x.又AE＝6，∴3x＝6，即x＝2.∴DE＝2.9．在Rt△ABC中，∠C＝90°，D为BC中点，DE⊥AB于E，且tanB＝12，AE＝6，求DE的长．解：设DE＝x，∵∠C＝90°，tanB＝12，∴BE＝2x.∴由勾股定理得BD＝5x.∴BC＝25x.又∵tanB＝12，∴AC＝5x.∴由勾股定理得AB＝5x.∴AE＝5x－2x＝3x.又AE＝6，∴3x＝6，即x＝2.∴DE＝2.10．等腰三角形的两边分别为6和8，求底角α的正切．解：如图，在△ABC中，AB＝AC，∠B＝∠C＝∠α，过A作AD⊥BC于D.(1)当AB＝6，BC＝8时，则CD＝4，∴AD为25.则底角tanα＝254＝52(2)当AB＝8，BC＝6时，则CD＝3，∴AD为55.则底角tanα＝553.10．等腰三角形的两边分别为6和8，求底角α的正切．解：如图，在△ABC中，AB＝AC，∠B＝∠C＝∠α，过A作AD⊥BC于D.(1)当AB＝6，BC＝8时，则CD＝4，∴AD为25.则底角tanα＝254＝52(2)当AB＝8，BC＝6时，则CD＝3，∴AD为55.则底角tanα＝553.