《两角和与差的正弦余弦正切公式》高一年级下册PPT课件（第1课时）.pptx

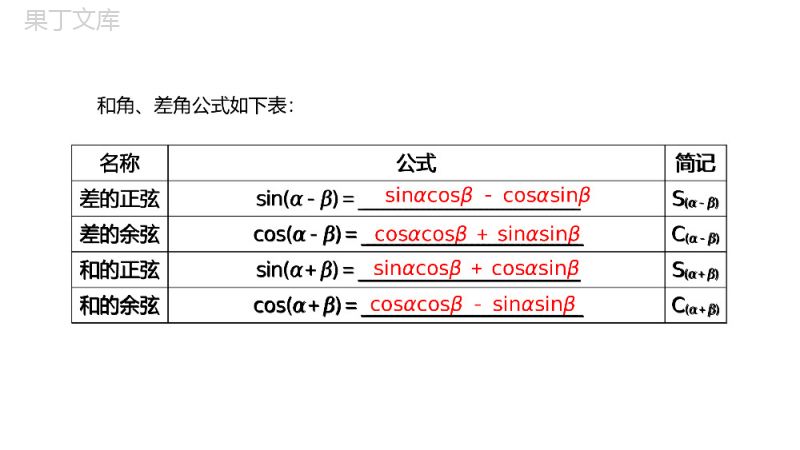
两角和与差的正弦、余弦和正切公式第三章三角恒等变换3.1.2两角和与差的正弦、余弦、正切公式第1课时两角和与差的正弦、余弦自主预习学案互动探究学案课时作业学案010203栏目导航CONTENT自主预习学案第三章三角恒等变换01变脸是川剧艺术中塑造人物的一种特技，演员在熟练的动作之间，奇妙地变换着不同的脸谱，用以表现剧中人物的情绪、心理状态的突然变化，达到“相随心变”的艺术效果，那么在三角函数中，两角和与差的正弦余弦之间又有怎样的变换呢？和角、差角公式如下表：sinαcosβ－cosαsinβ名称公式简记差的正弦sin(α－β)＝______________________________________S(α－β)差的余弦cos(α－β)＝______________________________________C(α－β)和的正弦sin(α＋β)＝______________________________________S(α＋β)和的余弦cos(α＋β)＝______________________________________C(α＋β)cosαcosβ＋sinαsinβsinαcosβ＋cosαsinβcosαcosβ－sinαsinβ名称公式简记差的正弦sin(α－β)＝______________________________________S(α－β)差的余弦cos(α－β)＝______________________________________C(α－β)和的正弦sin(α＋β)＝______________________________________S(α＋β)和的余弦cos(α＋β)＝______________________________________C(α＋β)第三章三角恒等变换[知识点拨]1.两角和差的余弦公式以及正弦公式的结构特点(1)公式中的α、β均为任意角．(2)两角和与差的正、余弦公式可以看成是诱导公式的推广，诱导公式可以看成是两角和与差的正、余弦公式的特例．(3)两角和与差的正弦公式结构是“正余余正，加减相同”，两角和与差的余弦公式结构是“余余正正，加减相反”．2．使用公式时不仅要会正用，还要能够逆用公式，如化简sin(α＋β)cosβ－cos(α＋β)sinβ时，不要将sin(α＋β)和cos(α＋β)展开，而应采用整体思想，进行如下变形：sin(α＋β)cosβ－cos(α＋β)sinβ＝sin[(α＋β)－β]＝sinα.这也体现了数学中的整体原则．√1．判断下列说法是否正确，正确的在后面的括号内打“√”，错误的打“×”．(1)sin(α±β)＝sinαcosβ±cosαsinβ对于任意角α，β均成立．()(2)不存在角α，β，使得sin(α－β)＝cosαcosβ－sinαsinβ.()(3)sin(α＋β)＝sinα＋sinβ一定不成立．()(4)已知sinα＝－35，α是第四象限角，则sin(π4－α)＝210.()×××1．判断下列说法是否正确，正确的在后面的括号内打“√”，错误的打“×”．(1)sin(α±β)＝sinαcosβ±cosαsinβ对于任意角α，β均成立．()(2)不存在角α，β，使得sin(α－β)＝cosαcosβ－sinαsinβ.()(3)sin(α＋β)＝sinα＋sinβ一定不成立．()(4)已知sinα＝－35，α是第四象限角，则sin(π4－α)＝210.()第三章三角恒等变换2．sin(30°＋45°)＝____________.[解析]sin(30°＋45°)＝sin30°cos45°＋cos30°·sin45°＝12×22＋32×22＝2＋64.2＋64[解析]sin(30°＋45°)＝sin30°cos45°＋cos30°·sin45°＝12×22＋32×22＝2＋64.2＋64互动探究学案第三章三角恒等变换02化简下列各式：(1)sin14°cos16°＋sin76°cos74°；(2)sinπ12.命题方向1公式的正用与逆用⇨典例1化简下列各式：(1)sin14°cos16°＋sin76°cos74°；(2)sinπ12.第三章三角恒等变换[解析](1)sin14°cos16°＋sin76°cos74°＝sin14°cos16°＋cos14°sin16°＝sin(14°＋16°)＝sin30°＝12.(2)sinπ12＝sin(π3－π4)＝sinπ3cosπ4－cosπ3sinπ4.＝32×22－12×22＝6－24.[解析](1)sin14°cos16°＋sin76°cos74°＝sin14°cos16°＋cos14°sin16°＝sin(14°＋16°)＝sin30°＝12.(2)sinπ12＝sin(π3－π4)＝sinπ3cosπ4－cosπ3sinπ4.＝32×22－12×22＝6－24.第三章三角恒等变换『规律总结』公式的巧妙运用①顺用：如本题中的(2)；②逆用：如本题中的(1)；③变用：变用涉及两个方面，一个是公式本身的变用，如cos(α＋β)＋sinαsinβ＝cosαcosβ，一个是角的变用，也称为角的拆分变换，如α＝(α＋β)－β，2α＝(α＋β)＋(α－β)等，从某种意义上来说，是一种整体思想的体现，如cos(α＋β)cosβ＋sin(α＋β)sinβ＝cos[(α＋β)－β]＝cosα.这些需要在平时的解题的中多总结，多研究，多留心．第三章三角恒等变换〔跟踪练习1〕求下列各式的值：(1)sin347°cos148°＋sin77°cos58°；(2)3sinπ12＋cosπ12.[解析](1)原式＝sin(360°－13°)cos(180°－32°)＋sin(90°－13°)cos(90°－32°)＝sin13°cos32°＋cos13°sin32°＝sin(13°＋32°)＝sin45°＝22.〔跟踪练习1〕求下列各式的值：(1)sin347°cos148°＋sin77°cos58°；(2)3sinπ12＋cosπ12.[解析](1)原式＝sin(360°－13°)cos(180°－32°)＋sin(90°－13°)cos(90°－32°)＝sin13°cos32°＋cos13°sin32°＝sin(13°＋32°)＝sin45°＝22.第三章三角恒等变换(2)原式＝232sinπ12＋12cosπ12＝2sinπ12cosπ6＋sinπ6cosπ12＝2sinπ12＋π6＝2sinπ4＝2.(2)原式＝232sinπ12＋12cosπ12＝2sinπ12cosπ6＋sinπ6cosπ12＝2sinπ12＋π6＝2sinπ4＝2.第三章三角恒等变换命题方向2给值求值⇨0典例2(1)已知α为锐角，sinα＝35，β是第四象限角，cosβ＝45，则sin(α＋β)＝______.(2)已知π2<β<α<3π4，cos(α－β)＝1213，sin(α＋β)＝－35，求sin2α的值．[思路分析](1)先求出cosα，sinβ的值，再代入公式S(α＋β)．(2)由α、β的范围，确定α－β，α＋β的范围，求出sin(α－β)、cos(α＋β)的值，再由2α＝(α－β)＋(α＋β)变形求值．(1)已知α为锐角，sinα＝35，β是第四象限角，cosβ＝45，则sin(α＋β)＝______.(2)已知π2<β<α<3π4，cos(α－β)＝1213，sin(α＋β)＝－35，求sin2α的值．[思路分析](1)先求出cosα，sinβ的值，再代入公式S(α＋β)．(2)由α、β的范围，确定α－β，α＋β的范围，求出sin(α－β)、cos(α＋β)的值，再由2α＝(α－β)＋(α＋β)变形求值．第三章三角恒等变换[解析](1)∵α为锐角，sinα＝35，∴cosα＝45.∵β为第四象限角，cosβ＝45，∴sinβ＝－35，sin(α＋β)＝sinαcosβ＋cosαsinβ＝35×45＋45×(－35)＝0.(2)因为π2<β<α<3π4，所以0<α－β<π4，π<α＋β<32π.[解析](1)∵α为锐角，sinα＝35，∴cosα＝45.∵β为第四象限角，cosβ＝45，∴sinβ＝－35，sin(α＋β)＝sinαcosβ＋cosαsinβ＝35×45＋45×(－35)＝0.(2)因为π2<β<α<3π4，所以0<α－β<π4，π<α＋β<32π.第三章三角恒等变换又cos(α－β)＝1213，sin(α＋β)＝－35，所以sin(α－β)＝1－cos2?α－β?＝1－?1213?2＝513，cos(α＋β)＝－1－sin2?α＋β?＝－1－?－35?2＝－45.所以sin2α＝sin[(α－β)＋(α＋β)]＝sin(α－β)cos(α＋β)＋cos(α－β)sin(α＋β)＝513×(－45)＋1213×(－35)＝－5665.又cos(α－β)＝1213，sin(α＋β)＝－35，所以sin(α－β)＝1－cos2?α－β?＝1－?1213?2＝513，cos(α＋β)＝－1－sin2?α＋β?＝－1－?－35?2＝－45.所以sin2α＝sin[(α－β)＋(α＋β)]＝sin(α－β)cos(α＋β)＋cos(α－β)sin(α＋β)＝513×(－45)＋1213×(－35)＝－5665.第三章三角恒等变换『规律总结』(1)当“已知角”有两个时，“所求角”一般表示为两个“已知角”的和或差的形式．(2)当“已知角”有一个时，此时应着眼于“所求角”与“已知角”的和或差的关系，然后应用诱导公式把“所求角”变成“已知角”．第三章三角恒等变换〔跟踪练习2〕(2018·济南外国语学校期中)若0<α<π2，－π2<β<0，cos(π4＋α)＝13，cos(π4－β2)＝33，求cos(α＋β2)．〔跟踪练习2〕(2018·济南外国语学校期中)若0<α<π2，－π2<β<0，cos(π4＋α)＝13，cos(π4－β2)＝33，求cos(α＋β2)．第三章三角恒等变换[解析]∵0<α<π2，∴π4<π4＋α<34π，∴sin(π4＋α)＝232，∵－π2<β<0，∴π4<π4－β2<π2，∴sin(π4－β2)＝63.cos(α＋β2)＝cos[(π4＋α)－(π4－β2)]＝cos(π4＋α)cos(π4－β2)＋sin(π4＋α)sin(π4－β2)＝13×33＋223×63＝539.[解析]∵0<α<π2，∴π4<π4＋α<34π，∴sin(π4＋α)＝232，∵－π2<β<0，∴π4<π4－β2<π2，∴sin(π4－β2)＝63.cos(α＋β2)＝cos[(π4＋α)－(π4－β2)]＝cos(π4＋α)cos(π4－β2)＋sin(π4＋α)sin(π4－β2)＝13×33＋223×63＝539.辅助角公式及其运用(1)公式形式：公式asinα＋bcosα＝a2＋b2sin(α＋φ)(或asinα＋bcosα)＝a2＋b2cos(α－φ)将形如asinα＋bcosα(a，b不同时为零)的三角函数式收缩为同一个角的一种三角函数式．(2)形式选择：化为正弦还是余弦，要看具体条件而定，一般要求变形后角α的系数为正，这样更有利于研究函数的性质．(1)公式形式：公式asinα＋bcosα＝a2＋b2sin(α＋φ)(或asinα＋bcosα)＝a2＋b2cos(α－φ)将形如asinα＋bcosα(a，b不同时为零)的三角函数式收缩为同一个角的一种三角函数式．(2)形式选择：化为正弦还是余弦，要看具体条件而定，一般要求变形后角α的系数为正，这样更有利于研究函数的性质．第三章三角恒等变换(1)2cosπ12＋6sinπ12的值是()A．2B．2C．22D．22(2)y＝cosx＋cos(x＋π3)的最大值是______.典例3B3(1)2cosπ12＋6sinπ12的值是()A．2B．2C．22D．22(2)y＝cosx＋cos(x＋π3)的最大值是______.3第三章三角恒等变换[解析](1)原式＝22(12cosπ12＋32sinπ12)＝22sin(π12＋π6)＝22sinπ4＝2，故选B．(2)y＝cosx＋cosx·12－sinx·32＝32cosx－32sinx＝3(32cosx－12sinx)＝－3(12sinx－32cosx)＝－3sin(x－π3)，当x＝2kπ－π6时，(k∈Z)，ymax＝3.[解析](1)原式＝22(12cosπ12＋32sinπ12)＝22sin(π12＋π6)＝22sinπ4＝2，故选B．(2)y＝cosx＋cosx·12－sinx·32＝32cosx－32sinx＝3(32cosx－12sinx)＝－3(12sinx－32cosx)＝－3sin(x－π3)，当x＝2kπ－π6时，(k∈Z)，ymax＝3.已知sinα＝55，sinβ＝1010，且α、β为锐角，求α＋β的值．由于角的范围过大致误典例4[错解]∵α为锐角，∴cosα＝1－sin2α＝255.又β为锐角，∴cosβ＝1－sin2β＝31010.∴sin(α＋β)＝sinαcosβ＋cosαsinβ＝55×31010＋255×1010＝22.已知sinα＝55，sinβ＝1010，且α、β为锐角，求α＋β的值．[错解]∵α为锐角，∴cosα＝1－sin2α＝255.又β为锐角，∴cosβ＝1－sin2β＝31010.∴sin(α＋β)＝sinαcosβ＋cosαsinβ＝55×31010＋255×1010＝22.第三章三角恒等变换由于0°<α<90°，0°<β<90°，所以0°<α＋β<180°，故α＋β＝45°或135°.[辨析]上述解法欠严密，仅由sin(α＋β)＝22以及0°<α＋β<180°就得到α＋β＝45°或α＋β＝135°是不正确的，因为角α、β的范围是有一定限制的，事实上sinα＝55<12，sinβ＝1010<12，故α<30°，β<30°，从而0°<α＋β<60°，故应仅有α＋β＝45°.为了避免出现上述失误我们可以选用两角和的余弦公式计算．[辨析]上述解法欠严密，仅由sin(α＋β)＝22以及0°<α＋β<180°就得到α＋β＝45°或α＋β＝135°是不正确的，因为角α、β的范围是有一定限制的，事实上sinα＝55<12，sinβ＝1010<12，故α<30°，β<30°，从而0°<α＋β<60°，故应仅有α＋β＝45°.为了避免出现上述失误我们可以选用两角和的余弦公式计算．第三章三角恒等变换[正解]∵α、β为锐角，sinα＝55，sinβ＝1010，∴cosα＝1－sin2α＝255，cosβ＝1－sin2β＝31010，∴cos(α＋β)＝cosαcosβ－sinαsinβ＝255×31010－55×1010＝22，∵α、β为锐角，∴0°<α＋β<180°，∴α＋β＝45°.[正解]∵α、β为锐角，sinα＝55，sinβ＝1010，∴cosα＝1－sin2α＝255，cosβ＝1－sin2β＝31010，∴cos(α＋β)＝cosαcosβ－sinαsinβ＝255×31010－55×1010＝22，∵α、β为锐角，∴0°<α＋β<180°，∴α＋β＝45°.第三章三角恒等变换[误区警示]此类题目是给值求角问题，解题的一般步骤是：(1)先确定角α的范围，且使这个范围尽量小；(2)根据(1)所得范围来确定求tanα、sinα、cosα中哪一个的值，尽量使所选函数在(1)得到的范围内是单调函数；(3)求α的一个三角函数值；(4)写出α的大小．1．计算sin43°cos13°－cos43°sin13°的结果等于()A．12B．33C．22D．32A[解析]∵sin43°cos13°－cos43°sin13°＝sin(43°－13°)＝sin30°＝12.∴选A．1．计算sin43°cos13°－cos43°sin13°的结果等于()A．12B．33C．22D．32[解析]∵sin43°cos13°－cos43°sin13°＝sin(43°－13°)＝sin30°＝12.∴选A．第三章三角恒等变换2．sin75°cos30°－sin15°sin150°的值等于()A．1B．12C．22D．32C[解析]原式＝cos15°cos30°－sin15°sin30°＝cos(15°＋30°)＝cos45°＝22.2．sin75°cos30°－sin15°sin150°的值等于()A．1B．12C．22D．32[解析]原式＝cos15°cos30°－sin15°sin30°＝cos(15°＋30°)＝cos45°＝22.课时作业学案第三章三角恒等变换03感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明谢谢观看新课标导学数学必修④·人教A版