《两角和与差的正弦余弦正切公式》高一年级下册PPT课件（第2课时）.pptx

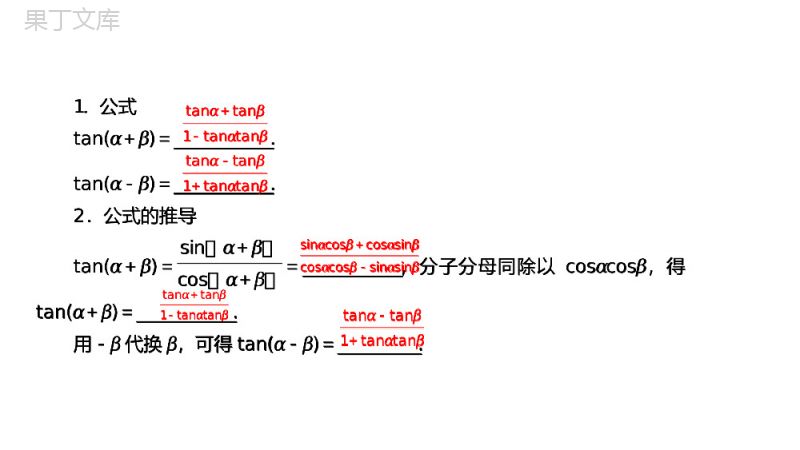
两角和与差的正弦、余弦和正切公式第三章三角恒等变换3.1.2两角和与差的正弦、余弦、正切公式第2课时两角和与差的正切自主预习学案互动探究学案课时作业学案010203栏目导航CONTENT自主预习学案第三章三角恒等变换01坐在教室里，需要一个合适视角才能看清楚黑板；在足球比赛中，若你从所守球门附近带球过人沿直线推进，要想把球准确地踢进大门去，需要确定一个最佳位置，这些实际生活中的问题可不是仅仅一个角度就可以解决的，其中涉及至少两个角度的因素，只有把问题分析全面，才能稳操胜券．怎样确定两角之间的关系呢？1．公式tan(α＋β)＝__________________.tan(α－β)＝__________________.2．公式的推导tan(α＋β)＝sinα＋βcosα＋β＝__________________，分子分母同除以cosαcosβ，得tan(α＋β)＝__________________.用－β代换β，可得tan(α－β)＝_______________.tanα＋tanβ1－tanαtanβtanα－tanβ1＋tanαtanβsinαcosβ＋cosαsinβcosαcosβ－sinαsinβtanα＋tanβ1－tanαtanβtanα－tanβ1＋tanαtanβ1．公式tan(α＋β)＝__________________.tan(α－β)＝__________________.2．公式的推导tan(α＋β)＝sinα＋βcosα＋β＝__________________，分子分母同除以cosαcosβ，得tan(α＋β)＝__________________.用－β代换β，可得tan(α－β)＝_______________.tanα＋tanβ1－tanαtanβtanα－tanβ1＋tanαtanβsinαcosβ＋cosαsinβcosαcosβ－sinαsinβtanα＋tanβ1－tanαtanβtanα－tanβ1＋tanαtanβ第三章三角恒等变换[知识点拨](1)适用条件：公式Tα±β只有在α≠π2＋kπ，β≠π2＋kπ，α±β≠π2＋kπ(k∈Z)时才成立，否则就不成立，这是由正切函数的定义域决定的．(2)特殊情况：当tanα或tanβ或tan(α±β)的值不存在时，不能使用Tα±β处理有关问题，但可改用诱导公式或其他方法．例如化简tan(π2－β)，因为tanπ2的值不存在，不能利用公式Tα－β，所以改用诱导公式来解．tan(π2－β)＝sinπ2－βcosπ2－β＝cosβsinβ.[知识点拨](1)适用条件：公式Tα±β只有在α≠π2＋kπ，β≠π2＋kπ，α±β≠π2＋kπ(k∈Z)时才成立，否则就不成立，这是由正切函数的定义域决定的．(2)特殊情况：当tanα或tanβ或tan(α±β)的值不存在时，不能使用Tα±β处理有关问题，但可改用诱导公式或其他方法．例如化简tan(π2－β)，因为tanπ2的值不存在，不能利用公式Tα－β，所以改用诱导公式来解．tan(π2－β)＝sinπ2－βcosπ2－β＝cosβsinβ.第三章三角恒等变换(3)正切公式的逆用及变形用①注意公式的逆用，比如：tanα＋β－tanα1＋tanα＋βtanα＝tan[(α＋β)－α]＝tanβ，又如1＋tanα1－tanα＝tan45°＋tanα1－tan45°tanα＝tan(45°＋α)．(3)正切公式的逆用及变形用①注意公式的逆用，比如：tanα＋β－tanα1＋tanα＋βtanα＝tan[(α＋β)－α]＝tanβ，又如1＋tanα1－tanα＝tan45°＋tanα1－tan45°tanα＝tan(45°＋α)．第三章三角恒等变换②除了公式的正用、逆用外，还要注意公式的变形应用tanα＋tanβ＝tan(α＋β)(1－tanαtanβ)，tanα－tanβ＝tan(α－β)(1＋tanαtanβ)，如tanα＋tanβ＋tanαtanβtan(α＋β)＝tan(α＋β)，tan(α＋β)－tanα－tanβ＝tanαtanβtan(α＋β)，1－tanαtanβ＝tanα＋tanβtanα＋β.1＋tanαtanβ＝tanα－tanβtanα－β.②除了公式的正用、逆用外，还要注意公式的变形应用tanα＋tanβ＝tan(α＋β)(1－tanαtanβ)，tanα－tanβ＝tan(α－β)(1＋tanαtanβ)，如tanα＋tanβ＋tanαtanβtan(α＋β)＝tan(α＋β)，tan(α＋β)－tanα－tanβ＝tanαtanβtan(α＋β)，1－tanαtanβ＝tanα＋tanβtanα＋β.1＋tanαtanβ＝tanα－tanβtanα－β.×1．判断下列说法是否正确，正确的在后面的括号内打“√”，错误的打“×”．(1)tan(α＋β)＝tanα＋tanβ1＋tanαtanβ.()(2)存在角α，β，使得tan(α－β)＝tanα－tanβ1－tanαtanβ.()(3)tan(π2＋π3)能根据公式tan(α＋β)直接展开．()(4)已知tanα＋tanβ＝2，tan(α＋β)＝4，则tanα·tanβ＝12.()√××1．判断下列说法是否正确，正确的在后面的括号内打“√”，错误的打“×”．(1)tan(α＋β)＝tanα＋tanβ1＋tanαtanβ.()(2)存在角α，β，使得tan(α－β)＝tanα－tanβ1－tanαtanβ.()(3)tan(π2＋π3)能根据公式tan(α＋β)直接展开．()(4)已知tanα＋tanβ＝2，tan(α＋β)＝4，则tanα·tanβ＝12.()第三章三角恒等变换2．若tanα＝2，tanβ＝12，则tan(α－β)＝()A．－34B．34C．3D．13B[解析]tan(α－β)＝tanα－tanβ1＋tanαtanβ＝2－121＋2×12＝34.2．若tanα＝2，tanβ＝12，则tan(α－β)＝()A．－34B．34C．3D．13[解析]tan(α－β)＝tanα－tanβ1＋tanαtanβ＝2－121＋2×12＝34.互动探究学案第三章三角恒等变换02如图，在平面直角坐标系xOy中，以Ox轴为始边作两个锐角α、β，它们的终边分别与单位圆交于A、B两点．已知A、B的横坐标分别为210、255.(1)求tan(α＋β)的值；(2)求α＋2β的值．命题方向1公式正用⇨典例1如图，在平面直角坐标系xOy中，以Ox轴为始边作两个锐角α、β，它们的终边分别与单位圆交于A、B两点．已知A、B的横坐标分别为210、255.(1)求tan(α＋β)的值；(2)求α＋2β的值．第三章三角恒等变换[思路分析]由题目可获取以下主要信息：①由任意角三角函数的定义可求cosα、cosβ；②α＋2β＝(α＋β)＋β.解答本题可先由任意角三角函数定义求cosα、cosβ，再求sinα、sinβ，从而求出tanα、tanβ，然后利用公式Tα＋β，求tan(α＋β)，最后利用α＋2β＝(α＋β)＋β，求tan(α＋2β)得到α＋2β的值．第三章三角恒等变换[解析](1)由三角函数的定义可知cosα＝210，cosβ＝255；所以sinα＝7210，sinβ＝55，所以tanα＝7，tanβ＝12，于是tan(α＋β)＝tanα＋tanβ1－tanαtanβ＝－3.(2)tan(α＋2β)＝tan[(α＋β)＋β]＝tanα＋β＋tanβ1－tanα＋βtanβ＝12＋－31－12×－3＝－1.又0<α<π2，所以0<α＋2β<32π，所以α＋2β＝34π.[解析](1)由三角函数的定义可知cosα＝210，cosβ＝255；所以sinα＝7210，sinβ＝55，所以tanα＝7，tanβ＝12，于是tan(α＋β)＝tanα＋tanβ1－tanαtanβ＝－3.(2)tan(α＋2β)＝tan[(α＋β)＋β]＝tanα＋β＋tanβ1－tanα＋βtanβ＝12＋－31－12×－3＝－1.又0<α<π2，所以0<α＋2β<32π，所以α＋2β＝34π.第三章三角恒等变换『规律总结』此类问题的解答首先要注意题目中的隐含条件，比如角的取值范围、三角函数值等；然后要注意寻找题目中各角的关系，比如α＋2β＝(α＋β)＋β等．第三章三角恒等变换〔跟踪练习1〕(1)tan(α－β)＝12，tanβ＝13，则tanα＝()A．1B．17C．15D．57(2)已知tan(α＋β)＝25，tan(β－π4)＝14，那么tan(α＋π4)等于()A．1318B．1322C．322D．318AC〔跟踪练习1〕(1)tan(α－β)＝12，tanβ＝13，则tanα＝()A．1B．17C．15D．57(2)已知tan(α＋β)＝25，tan(β－π4)＝14，那么tan(α＋π4)等于()A．1318B．1322C．322D．318第三章三角恒等变换[思路分析](2)利用角α＋π4＝(α＋β)－(β－π4)之间的关系求解．[解析](1)tanα＝tan[(α－β)＋β]＝tan?α－β?＋tanβ1－tan?α－β?tanβ＝12＋131－12×13＝1.[思路分析](2)利用角α＋π4＝(α＋β)－(β－π4)之间的关系求解．[解析](1)tanα＝tan[(α－β)＋β]＝tan?α－β?＋tanβ1－tan?α－β?tanβ＝12＋131－12×13＝1.第三章三角恒等变换(2)tan(α＋π4)＝tan[(α＋β)－(β－π4)]＝tanα＋β－tanβ－π41＋tanα＋βtanβ－π4＝25－141＋25×14＝322.(2)tan(α＋π4)＝tan[(α＋β)－(β－π4)]＝tanα＋β－tanβ－π41＋tanα＋βtanβ－π4＝25－141＋25×14＝322.第三章三角恒等变换求下列各式的值：命题方向2公式的逆用及变形应用⇨典例2(1)1－tan75°1＋tan75°；(2)(1＋tan1°)(1＋tan2°)…(1＋tan44°)；(3)tan25°＋tan35°＋3tan25°tan35°.(1)1－tan75°1＋tan75°；(2)(1＋tan1°)(1＋tan2°)…(1＋tan44°)；(3)tan25°＋tan35°＋3tan25°tan35°.第三章三角恒等变换[思路分析]尝试使用两角和与差的正切公式及其变形式对原式进行变形求值．[解析](1)原式＝tan45°－tan75°1＋tan45°tan75°＝tan(45°－75°)＝－33.(2)因为(1＋tan1°)(1＋tan44°)＝1＋tan1°＋tan44°＋tan1°×tan44°＝2，同理(1＋tan2°)(1＋tan43°)＝2，…，所以原式＝222.[解析](1)原式＝tan45°－tan75°1＋tan45°tan75°＝tan(45°－75°)＝－33.(2)因为(1＋tan1°)(1＋tan44°)＝1＋tan1°＋tan44°＋tan1°×tan44°＝2，同理(1＋tan2°)(1＋tan43°)＝2，…，所以原式＝222.第三章三角恒等变换(3)∵tan60°＝tan(25°＋35°)＝tan25°＋tan35°1－tan25°tan35°＝3，∴tan25°＋tan35°＝3(1－tan25°tan35°)∴tan25°＋tan35°＋3tan25°tan35°＝3.『规律总结』1.“1”的代换：在Tα±β中如果分子中出现“1”常利用1＝tan45°来代换，以达到化简求值的目的．2．若α＋β＝π4＋kπ，k∈Z，则有(1＋tanα)(1＋tanβ)＝2.3．若化简的式子里出现了“tanα±tanβ”及“tanαtanβ”两个整体，常考虑tan(α±β)的变形公式．(3)∵tan60°＝tan(25°＋35°)＝tan25°＋tan35°1－tan25°tan35°＝3，∴tan25°＋tan35°＝3(1－tan25°tan35°)∴tan25°＋tan35°＋3tan25°tan35°＝3.『规律总结』1.“1”的代换：在Tα±β中如果分子中出现“1”常利用1＝tan45°来代换，以达到化简求值的目的．2．若α＋β＝π4＋kπ，k∈Z，则有(1＋tanα)(1＋tanβ)＝2.3．若化简的式子里出现了“tanα±tanβ”及“tanαtanβ”两个整体，常考虑tan(α±β)的变形公式．第三章三角恒等变换〔跟踪练习2〕求值：(1)1＋tan105°1－tan105°；(2)(3＋tan30°tan40°＋tan40°tan50°＋tan50°tan60°)·tan10°.[解析](1)原式＝tan45°＋tan105°1－tan45°tan105°＝tan(45°＋105°)＝tan150°＝－33.〔跟踪练习2〕求值：(1)1＋tan105°1－tan105°；(2)(3＋tan30°tan40°＋tan40°tan50°＋tan50°tan60°)·tan10°.[解析](1)原式＝tan45°＋tan105°1－tan45°tan105°＝tan(45°＋105°)＝tan150°＝－33.第三章三角恒等变换(2)原式＝(1＋tan30°tan40°＋1＋tan40°tan50°＋1＋tan50°tan60°)tan10°，∵tan10°＝tan(40°－30°)＝tan40°－tan30°1＋tan40°tan30°∴1＋tan30°tan40°＝tan40°－tan30°tan10°.同理，1＋tan40°tan50°＝tan50°－tan40°tan10°，1＋tan50°tan60°＝tan60°－tan50°tan10°.∴原式＝(tan40°－tan30°tan10°＋tan50°－tan40°tan10°＋tan60°－tan50°tan10°)tan10°＝tan40°－tan30°＋tan50°－tan40°＋tan60°－tan50°＝－tan30°＋tan60°＝－33＋3＝233.(2)原式＝(1＋tan30°tan40°＋1＋tan40°tan50°＋1＋tan50°tan60°)tan10°，∵tan10°＝tan(40°－30°)＝tan40°－tan30°1＋tan40°tan30°∴1＋tan30°tan40°＝tan40°－tan30°tan10°.同理，1＋tan40°tan50°＝tan50°－tan40°tan10°，1＋tan50°tan60°＝tan60°－tan50°tan10°.∴原式＝(tan40°－tan30°tan10°＋tan50°－tan40°tan10°＋tan60°－tan50°tan10°)tan10°＝tan40°－tan30°＋tan50°－tan40°＋tan60°－tan50°＝－tan30°＋tan60°＝－33＋3＝233.是否存在锐角α和β，使得下列两式(1)α＋2β＝23π(2)tanα2tanβ＝2－3同时成立？典例3[思路分析]解答本题关键是从(1)中得出α2＋β＝π3，从而与(2)建立关系．[解析]存在φ＝π6，β＝π4，使(1)(2)同时成立．假设存在符合题意的锐角α和β，是否存在锐角α和β，使得下列两式(1)α＋2β＝23π(2)tanα2tanβ＝2－3同时成立？[思路分析]解答本题关键是从(1)中得出α2＋β＝π3，从而与(2)建立关系．[解析]存在φ＝π6，β＝π4，使(1)(2)同时成立．假设存在符合题意的锐角α和β，第三章三角恒等变换由(1)知：α2＋β＝π3，∴tan(α2＋β)＝tanα2＋tanβ1－tanα2tanβ＝3，由(2)知tanα2tanβ＝2－3，∴tanα2＋tanβ＝3－3，∴tanα2，tanβ是方程x2－(3－3)x＋2－3＝0的两个根，由(1)知：α2＋β＝π3，∴tan(α2＋β)＝tanα2＋tanβ1－tanα2tanβ＝3，由(2)知tanα2tanβ＝2－3，∴tanα2＋tanβ＝3－3，∴tanα2，tanβ是方程x2－(3－3)x＋2－3＝0的两个根，第三章三角恒等变换得x1＝1，x2＝2－3.∵0<α<π2，则0