十字相乘法,十字相乘法公式技巧

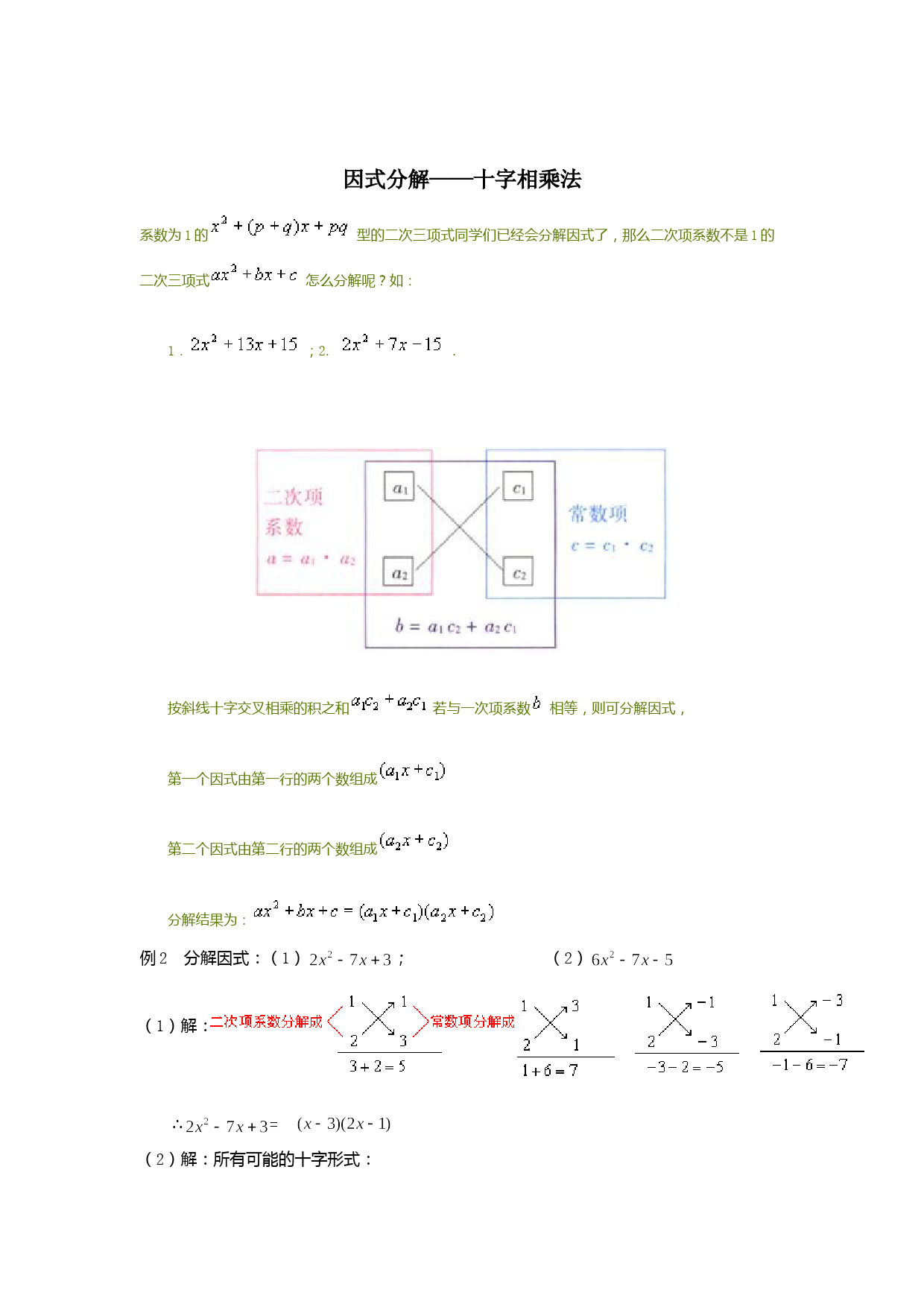
('因式分解——十字相乘法系数为1的型的二次三项式同学们已经会分解因式了，那么二次项系数不是1的二次三项式怎么分解呢？如：1．；2..按斜线十字交叉相乘的积之和若与一次项系数相等，则可分解因式，第一个因式由第一行的两个数组成第二个因式由第二行的两个数组成分解结果为：例2分解因式：（1）；（2）（1）解：∴=（2）解：所有可能的十字形式：∴说明：⑴二次项系数为正时，只考虑分解成两个正因数之积；⑵在二次项系数为正时，常数项的分解，符号规律同上节、的符号规律；⑶分解二项项系数、常数项有多种可能，即使对于同一种分解，十字图也有不同的写法，为了避免重或漏，故二次项系数的因数一经排定就不变，而用常数项的因数作调整；⑷用十字相乘法分解因式时，一般要经过多次尝试才能确定能否分解或怎样分解．练习题（因式分解）：（1）2x2＋7x＋3=___________（2）3x2－5x＋2=___________（3）2x2＋5x－7=___________（4）5x2－3x－2=___________二、练一练、做一做：1、把下列各式分解因式：（1）（2）（3）（4）(a＋b)2＋5(a＋b)－362、将下列各式因式分解（1）（2）（3）（4）3、将下列各式因式分解（1）；（2）2x2＋5x＋2；（3）)3x2＋7x－6；（4）2x2－5xy＋2y24、用因式分解法列下列方程:（1）x2+2x－3=0（2）2x2－7x+6=0（3）x(x－2)=3（4）(2x－3)2+3(2x－3)+2=0.因式分解之十字相乘法专项练习题(1)a2－7a+6；(2)8x2+6x－35；(3)18x2－21x+5；(4)20－9y－20y2；(5)2x2+3x+1；(6)2y2+y－6；(7)6x2－13x+6；(8)3a2－7a－6；(9)6x2－11x+3；(10)4m2+8m+3；(11)10x2－21x+2；(12)8m2－22m+15；(13)4n2+4n－15；(14)6a2+a－35；(15)5x2－8x－13；(16)4x2+15x+9；(17)15x2+x－2；(18)6y2+19y+10；(19)2(a+b)2+(a+b)(a－b)－6(a－b)2；(20)7(x－1)2+4(x－1)－20；参考答案：(1)(a-6)(a-1)，(2)(2x+5)(4x-7)(3)(3x-1)(6x-5)，(4)-(4y-5)(5y+4)(5)(x+1)(2x+1)，(6)(y+2)(2y-3)(7)(2x-3)(3x-2)，(8)(a-3)(3a+2)(9)(2x-3)(3x-1)，(10)(2m+1)(2m+3)(11)(x-2)(10x-1)，(12)(2m-3)(4m-5)(13)(2n+5)(2n-3)，(14)(2a+5)(3a-7)(15)(x+1)(5x-13)，(16)(x+3)(4x+3)(17)(3x-1)(5x=2)，(18)(2y+5)(3y+2)(19)(3a-b)(5b-a)，(20)(x+1)(7x-17)',)