层次分析法--简单案例分析,层次分析法简单案例分析

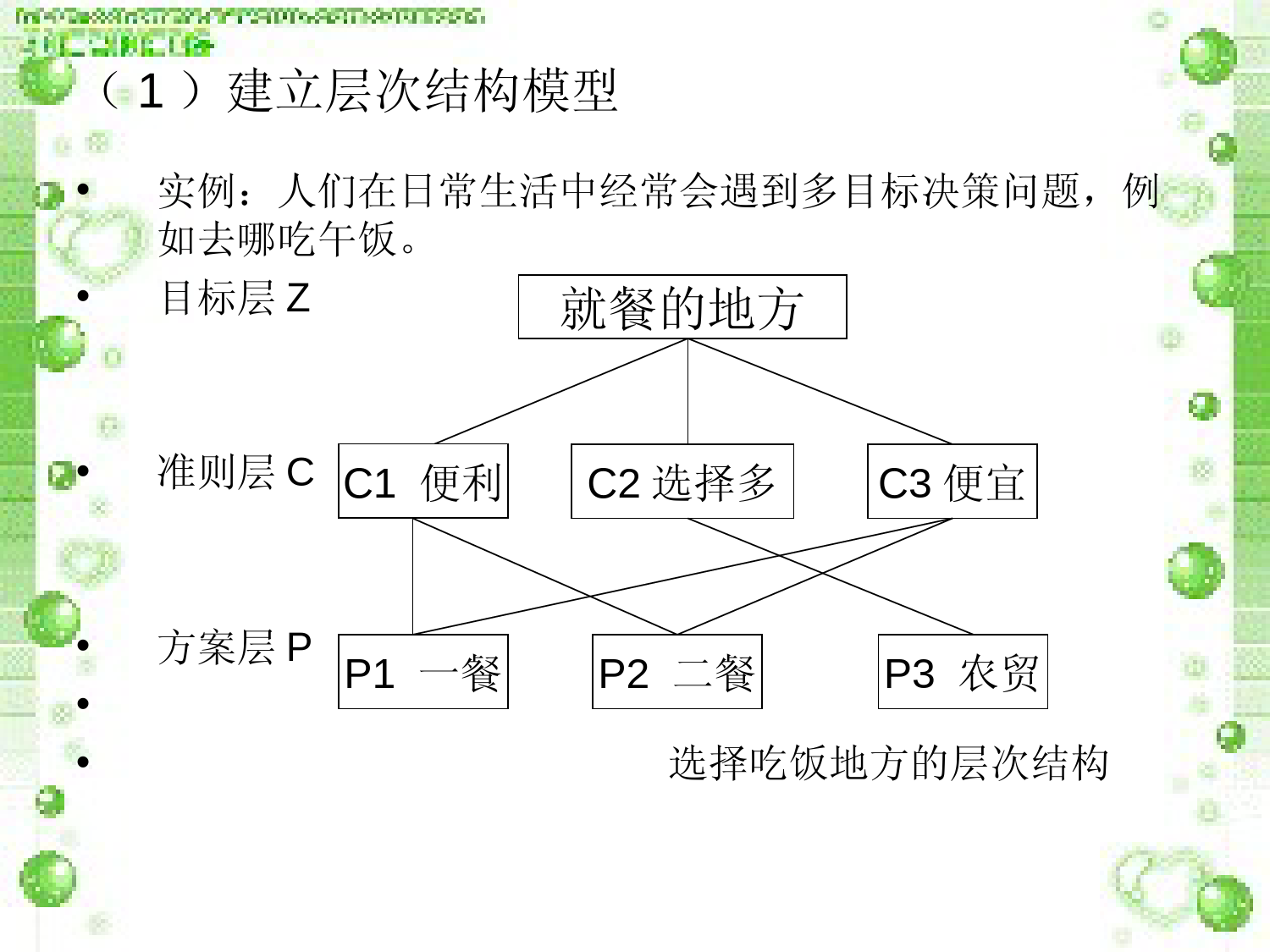
层次分析法•AnalyticHierarchyProcess(AHP)•1、层次分析法的简介•2、层次分析法的基本原理•3、层次分析法的基本步骤与我的案例分析宁波大学海运学院一.层次分析法的简介•层次分析法（AnalyticHierarchyProcess，简称AHP）是将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。•该方法是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代初，在为美国国防部研究“根据各个工业部门对国家福利的贡献大小而进行电力分配”课题时，应用网络系统理论和多目标综合评价方法，提出的一种层次权重决策分析方法。•层次分析法的特点是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上，利用较少的定量信息使决策的思维过程数学化，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。尤其适用于对决策结果难于直接准确计算的场合。二.层次分析法的基本原理•先分解后综合•整理和综合人们的主观判断，使定性分析与定量分析有机结合，实现定量化决策。•首先将所要分析的问题层次化，根据问题的性质和要达到的总目标，将问题分解成不同的组成因素，按照因素间的相互关系及隶属关系，将因素按不同层次聚集组合，形成一个多层分析结构模型，最终归结为最低层（方案、措施、指标等）相对于最高层（总目标）相对重要程度的权值或相对优劣次序的问题。三.层次分析法的基本步骤与我的案例•（1）建立层次结构模型；•（2）构造判断矩阵；•（3）层次单排序；•（4）一致性检验；•（5）层次总排序。（1）建立层次结构模型•实例：人们在日常生活中经常会遇到多目标决策问题，例如去哪吃午饭。•目标层Z•准则层C•方案层P••选择吃饭地方的层次结构就餐的地方C1便利C2选择多C3便宜P3农贸P1一餐P2二餐（2）构造判断矩阵•通过相互比较确定各准则对于目标的权重，即构造判断矩阵。在层次分析法中，为使矩阵中的各要素的重要性能够进行定量显示，引进了矩阵判断标度（1～9标度法）:标度含义1表示两个元素相比，具有同样的重要性3表示两个元素相比，前者比后者稍重要5表示两个元素相比，前者比后者明显重要7表示两个元素相比，前者比后者极其重要9表示两个元素相比，前者比后者强烈重要2,4,6,8表示上述相邻判断的中间值aij表示：i相对j来讲的比较结果（重要性），aii=1aji=1/aijA-C判断矩阵•计算得：λmax=3.039CI=λmax-n/n-1=0.0195CR=CI/RI=0.037＜0.1表明该判断矩阵通过一致性检验，具有满意一致性AC1C2C3C1153C21/511/3C31/331构造所有相对于不同准则的方案层判断矩阵相对与便宜C1-P判断矩阵计算得：λmax=3.039CI=λmax-n/n-1=0.0195CR=CI/RI=0.037表明该判断矩阵通过一致性检验，具有满意一致性C1P1P2P3P1135P21/313P31/51/31相对于选择多C2-P判断矩阵•计算得：λmax=3.018CI=λmax-n/n-1=0.009CR=CI/RI=0.018＜0.1表明该判断矩阵通过一致性检验，具有满意一致性C2P1P2P3P111/41/8P2411/3P3831相对于便宜C3-P判断矩阵•计算得：λmax=3.002CI=λmax-n/n-1=0.001CR=CI/RI=0.001＜0.1表明该判断矩阵通过一致性检验，具有满意一致性C2P1P2P3P111/41/8P2411/3P3831权重0.6330.1060.260P10.6330.0740.236P20.2600.2570.682P30.1060.6990.082层次总排序=经过计算得：P1一餐权值为：0.470,P2二餐权值为：0.370P3农贸权值为：0.160决策结果：吃饭首选地是一餐，其次是二餐，再次是农贸。层次总排序权值：P1:0.470,P2:0.370,P3:0.160