3、动量矩定理及其守恒定律,动量矩定理和动量矩守恒定律
本作品内容为3、动量矩定理及其守恒定律,格式为 doc ,大小 2441256 KB ,页数为 9页

('3、动量矩定理及其守恒定律描写质点组运动规律的三个基本定理,我们已经讲了其中的一个基本定理,也就是质点组的动量定理,我们还由质点组动量定理导出了质点组的动量守恒规律和质心运动定理。下面准备要讲的是关于质点组整体运动规律的另外二个基本定理,即动量矩定理与动能定理。现在先讲质点组的动量矩定理与动量矩守恒规律。动量矩的概念我们在质点力学部分已经有过接触。在讨论质点的动量矩定理时,我曾经强调过一提到取矩,不管是计算动量矩也好,还是计算力矩也好,首先必需要明确指出以那一点为取矩的中心,或者对那一轴取矩。对质点如此,那么对质点组也得如此,讨论质点组的动量矩也同样要首先指出以那点为取矩中心,现在我们就先以任一固定点为取矩中心,推出:一、质点组对固定点o的动量矩定理:1、质点组动量矩的定义:假设由n个质点组成的质点组,其中第i个质点对固定点0的矢径,定义质点组的总动量矩等于组内所有质点对固定点0的动量矩的矢量和,即:。这就是质点组动量矩的定义式。与质点组动量定理的推导相类似,质点组的动量矩定理也可以由牛顿第二定理直接导出:根据牛顿第二定律得质点组中第i个质点的动力学方程为:,用乘等式的两边:并对n个这样类似的方程求和,则有:……(1)此等式的右边的第一项是质点组内所有内力对固定点的力矩的矢量和。可以证明这项矢量和必定等于零。为了推算简单起见。先证明i,j两个质点所受的一对内力对固定点O的力矩的矢量和等于零。证明:如图所示,质点组内i,j两个质点的相互作用的内力为:j对i的作用力为,它的反作用力作用在j上,用表示。因为它们是一对作用与反作用力,所以=-。O为任意一固定点。这两个力对O点的力矩矢量和就是。因为这两个矢量在同一方向上,所以=0。另外我们所取的两个质点是任意的,所以上面得到的结果对质点组中任意二个质点都成立。既然成对的内力矩等于零,而总内力矩正是一一成对的内力矩之和。所以由此可以推理得到:质点组中所有的内力对任一固定点0的力矩之和恒等于零。即:,又因为将它们代入(1)式则有这里的是质点的总动量距.所以它可写成为:令则又可简写为这就是质点组动力学的第二个基本定理叫做质点组的动量矩定理。它表明质点组对任一固定点的动量矩对时间的变化率,就等于作用在质点组上所有外力对该固定点的力矩的矢量和。它在以固定点O为原点的固定直角坐标系上的三个分量式为:动量矩定理的这三个分量式说明了什么物理意义?说明了质点组对某一固定轴的动量矩对时间的变化率,等于作用在质点组上的所有外力对该轴的力矩之和。由这个定理我们再一次看到内力是不能改变质点组整体的动量矩,只有外力才有可能引起质点组的总动量矩的变化。由质点组的动量矩定理可直接推出质点组的动量矩守恒定律。二、动量矩守恒定律:如果作用在质点组上的所有外力对固定点的力矩之和等于零:由动量矩定理可得其第一积分为:。可见对同一固定点质点组的动量矩守恒,总动量矩等于恒矢量。这个关系就是质点组的动量矩守恒定律。要注意力矩之和等于零并不意味着外力之和一定等于零,这句话反过来说也不成立,也就是说外力之和等于零并不意味着外力矩之和等于零。为什么道理?我不讲了。留给大家课外去思考。与动量守恒的情形类似,如果作用在质点组上所有外力对某固定点的力矩之和虽然不等于零,但是,对通过该定点的某一固定轴例如x轴的力矩之和为零,即时,则质点组的动量矩在这一轴上的分量是守恒的,等于一常量,即。上面推导得到的质点组的动量矩定理和动量矩守恒定律只对惯性系中的固定点或固定轴成立。如果我们选择质点组的质心为取矩中心,这时质点组相对质心(坐标系)的动量矩的变化将遵循咋样的规律呢?现在我们就着手研究这个问题,也就是推出质点组对质心的动量矩定理。三、质点组对质心的动量矩定理:1、推导:假设由n个质点组成的质点组中C点是它的质心,取质心为一坐标原点,并固定一坐标系,它随着质心一起相对固定坐标系平动。如果质心有加速度时,平动坐标系就具有加速度,此时它就不再是惯性系,质点组上每个质点都将受到惯性力的作用,所以质点组对质心的动量矩定理得从非惯性系的动力学方程导出。除此之外,我们也可以根据用坐标转换的关系,再根据质点组对固定点的动量矩定理推出质点组对质心的动量矩定理。前一种方法就是我们课本上介绍的那种方法。前一种方法我在课堂上就不讲了,大家课外自己可以去看书。现在我们就采用后一种方法来推出质点组对质心的动量矩定理。如上图所示,质点组中任一质点i其质量为。此质点组对固定坐标原点的位置矢径为,相对质心的位置矢径用表示,质心C相对固定点O的位置矢径为。根据矢量合成定理可得:……(1)已知质点组相对固定点O的动量矩定理是:……(2)将(1)代入(2)式的左边:即……(3)可以证明第2和第3两项都等于0。,然而对质心坐标系来说,那么根据质心的定义式知,也就等于0。于是可知这就证明第2和第3两项确实都等于0。再将(1)代入(2)式的右边则有:根据质心运动定理知:它又等于……(4)我们将得到的结果(3)(4)代入(2)式则有:由所得到的这个最后结果可以看出:是质点组对质心的总动量矩。可用符号表示,所以等式的左侧就是质点组对质心的动量矩对时间的一阶微商,而等式的右侧是作用在质点组上的所有外力对质心C的力矩矢量和,用符号表示的话,上式就可简写为:——此等式就是质点组相对质心平动参照系的动量矩定理,简称为质点组对质心的动量矩定理。这里要注意质心平动参照系它不一定是惯性系。因为我们前面的推导没有对它是不是惯性系加过限止,所以它有可能是非惯性系,也就是说,质心的动量矩定理对质心平动参照系是不是惯性系都是成立的。将它与对固定点O的动量矩定理:相比较,可见他们具有完全相同的形式,唯一的区别是两者的取矩中心不同,一个是以质心为取矩中心,一个是以固定点为取矩中心。总之,2、结论:质点组的动量矩对时间的一阶微商等于作用在质点组上的所有外力矩之和。这个结论不仅对惯性系中的固定点成立,对质心也是成立的,但是对其它的动点一般是不成立的。如图所示,如果我们将平动(参照)坐标系固定在非质心的其它动点上,在此情况下质点组中任一质点的位置矢径在定、动坐标系中的关系应该是:,质心位置矢径的关系是:。与推导质点组对质心的动量距定理的方法一样,不难推出质点组对动点的动量距的变化规律,在课堂上我不再详细的推导了,只给出他的结果,有兴趣的同学不妨课外去推导一下,也是有好处的,不感兴趣的就不用勉强了。由推导得到的结果是。有的书上管这个关系式,叫质点组对动点的动量矩定理。由这个关系式可以看出,它与我们刚才所讲的结论一般是不相符合的,他多了一项惯性力矩在质心平动坐标系中这一项刚好是等于零的,虽然各质点都要受到惯性力的作用,但是这些力对质心的惯性力矩刚好是相互抵消的,在对质心的动量矩定理中就不存在这一项惯性力矩,但是对于其它动点的平动坐标系这项惯性力矩一般是等于零的,只有当动点的加速度与共线或则是平行时,它才等于零,也只有在这样特殊的情况下,上面讲过的结论对动点才适用。所以说在一般情况下,上面的结论对动点一般是不成立的。与相对固定点的动量矩守恒定律一样,我们也可由对质心的动量矩定理推出对质心动量矩守恒定律。4、对质心的动量距守恒定律:如果,外力对质心的力矩的矢量和则。5、最后再讲一下引进质点组对质心的动量矩定理的实际意义:(1)质点组的动量矩定理是讨论钢体转动的基础,[这里指的是相对固定坐标系](2)而质点组对质心的动量矩定理是讨论刚体相对于质心的转动的基础。(3)因为刚体的一般运动,总可以看成质心的运动,加上相对于质心运动。刚体的质心运动规律完全可由质心运动定理来讨论,刚体相对于质心的运动要由对质心的动量矩定理来解决。因此,这就是讨论质心动量矩定理的最大意义所以我们为什么一开始讨论质点组问题就要引进质心的概念,它的重要性也就在于此。关于描写质点组整体运动规律的第二个基本定理就讨论到这里为止。接下去讨论最后一个基本定理,也就是:质点组的§4、动能定理与机械能守恒定律一、对固定点的动能定理:——对惯性系讨论的程序与讨论动量矩定理的情形一样,先来推出两点组对固定点的动能定理,也就是对惯性系的动能定理。已知一个质点的动能等于,那么对由n个质点组成的总动能,当然就等于组内所有质点的动能之和,即质点组的动能,——是质点组中任一质点对固定点的速度的平方。在惯性系中,质点组的动能T的微dT就等于作用在质点组上的所有外力和内力所作主功之和:,这个结论就是质点组对固定点的动能定理,这里的就是质点组内任一质点对固定点的位矢。下面我们就来证明这个结论。证明:从质点的动能定理出发可得任一质点的动能微分:将此式的两边对i求和,从i=1到n的求和,则有:此等式左边括号的量正好是质点组的动能,所以左边就是质点组的动能的微分,可见它就是我们所要证明的质点组的动能定理。在这里要注意动能定理中内力所作的元功之和一般来讲是不等于零的,这一点与质点组的动量定理及动量矩定理是不同的。在前面两个定理中内力及内力矩的矢量和均等于零而去掉的。我们不能以此一概而论之,把质点组动能定理中的内力之功也给去掉,在一般情况下不能去掉,只有对刚体这种特殊情况下内力之功才为零。下面就以任意两个质点的情况来加以说明内力之功一般不等于零。假设质点组中的任意两个质点和,它们对固定点O的矢径分别为和,彼此相互作用的力为和[如下图所示],这两个相互作用的内力所作元功之和就等于从A到B的矢量是矢量的变化量,它既包括方向的变化,但又包括大小的变化,当大小不变而改变方向时,只能垂直于:,与共线,所以只能于是有:。只有刚体才能符合这种特殊情况,我们课本上的讲法是错误的,大家翻到课文P.123的机械能守恒律上面的倒数第二行,而意味着质点间距离不能改,即为刚体,这样的说法是错的。对于刚体来说质点间的距离不变,只说明大小的变化。运动刚体的的,只有刚体静止时,才等于零。而我们讨论的是动力学问题,所以是不存在((后一种情况的静止的情况。应将课本上的改为))。对一般质点组来说,质点间的距离往往是变化的,所以内力所作之功的总和不一定等于零。正是这个原因可以用来定性解释许多实际问题。例如,一颗定时炸弹,开始时是静止时,它的动能当然是等于零的,当它爆炸时,显然它的动能是不等于零的。它的动能从那儿来的呢?它的动能就是靠内力作功获得的。讲到这里我倒想起了在中学里教书的一个同学曾经问过我一个问题,他说自己百思不解,问过其他同校老师也得不到满意的解释,其实这个问题很简单。一点也不难。只要一句话就可以解决。他提出的问题是一个常见实际问题。汽车从静止到运动它的动能是从哪儿来的?就是这样一个问题。我的同学开始的时候认为汽车的动能好像是由牵引力作功获得的?[中学里有些老往往这样含糊地回答学生]。但是仔细一分析毛病就出来了,所谓汽车的牵引力实际上就是汽车的主动轮(即后轮)受到的向前的静摩擦力与从动轮受到向后的静摩擦力之差。而静摩擦力是不作功的,而且压力、重力都是不作功的。那么汽车的动能就不可能增加,但实际现象明摆着汽车动能是增加的。分析到这里我同学说自己就百思不得其解了。问我应如何解决这个问题。这个问题问我们在坐的同学应该是个很容易回答的问题吧?这个问题最关键是,不能把汽车整体当作刚体,因为汽车整体不是刚体,它内力所作的功不等于零。所以汽车的动能会增加,类似的实际问题很多,例如自行车的加速运动,人从地面跳起等等实际现象都可以用内力要作功来加以解释……。二.械能守恒定律:由质点组的动能定理可以直接导出质点组的机械能守恒定律。如果,作用在质点组上的所有外力和内力都是保守力或者保守力所作元功的代数和等于零时,根据势能定义可知内外保守力所作元功就等于与其保守力相关的势能微分的负值。即:根据动能定理有:对此式积分可得:,这就是质点组的机械能守恒定律。应用时一定要注意它的守恒条件:内、外力均是保守力[光有外力是保守力是不够的]或者非保守力所作之功的代数和等于零。',)
提供3、动量矩定理及其守恒定律,动量矩定理和动量矩守恒定律会员下载,编号:1700753431,格式为 docx,文件大小为9页,请使用软件:wps,office word 进行编辑,PPT模板中文字,图片,动画效果均可修改,PPT模板下载后图片无水印,更多精品PPT素材下载尽在某某PPT网。所有作品均是用户自行上传分享并拥有版权或使用权,仅供网友学习交流,未经上传用户书面授权,请勿作他用。若您的权利被侵害,请联系963098962@qq.com进行删除处理。

 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载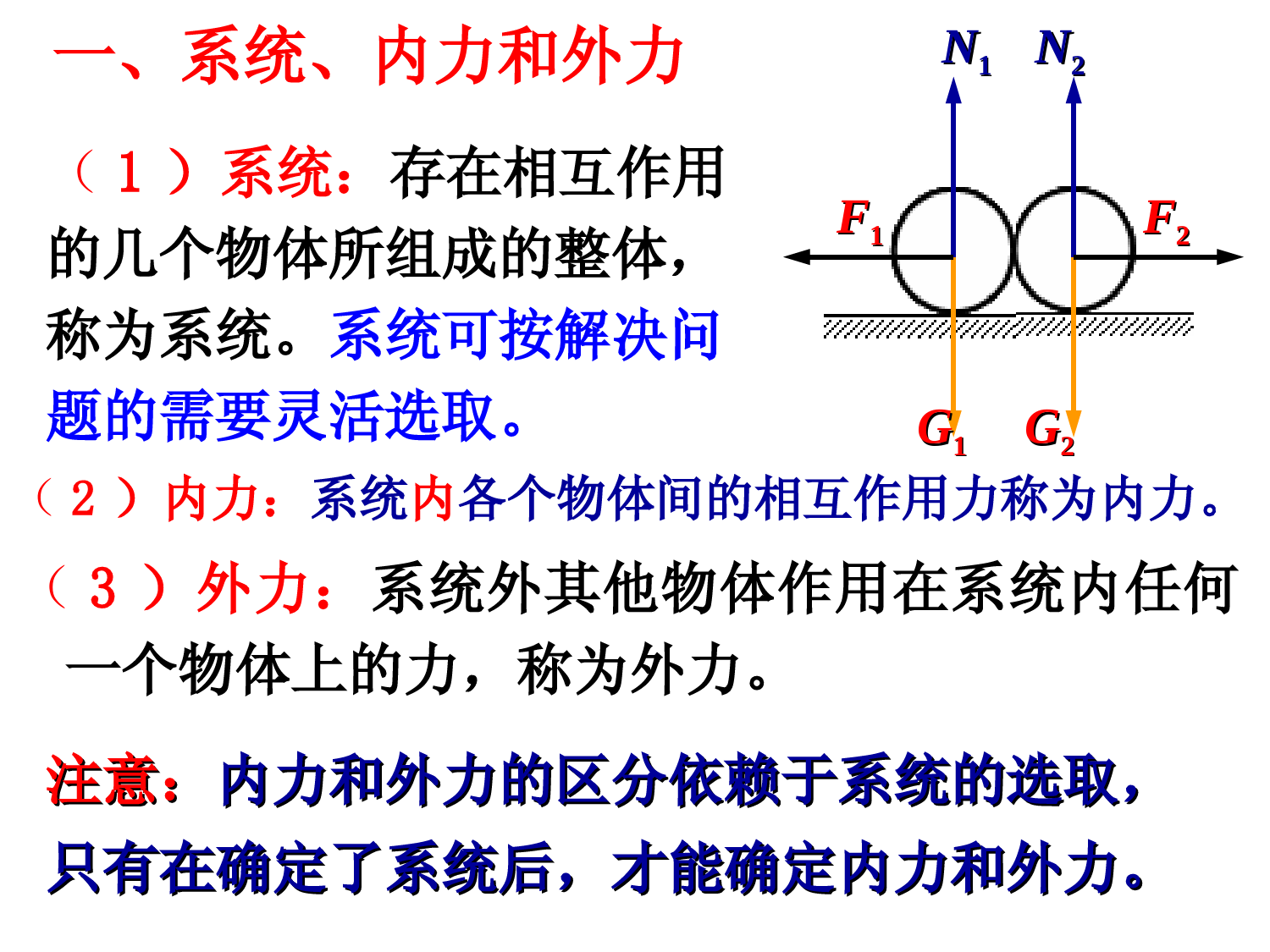 下载
下载 下载
下载 下载
下载 下载
下载