12021-2022优化方案数学-选择性必修-第一册
本作品内容为12021-2022优化方案数学-选择性必修-第一册,格式为 doc ,大小 389160 KB ,页数为 9页

('[A基础达标]1.若异面直线l1的方向向量与l2的方向向量的夹角为150°,则l1与l2所成的角为()A.30°B.150°C.30°或150°D.以上均不对解析:选A.直线l1与l2所成的角与其方向向量的夹角相等或互补,且异面直线所成角的范围为(0,90°].应选A.2.在长方体ABCDA1B1C1D1中,AB=2,BC=2,DD1=3,则AC与BD1所成角的余弦值为()A.0B.C.-D.解析:选A.以D为原点,建立如图所示的空间直角坐标系,则D1(0,0,3),B(2,2,0),A(2,0,0),C(0,2,0).所以BD1=(-2,-2,3),AC=(-2,2,0).所以cos〈BD1,AC〉==0.3.如图,在长方体ABCDA1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的正弦值为()A.B.C.D.解析:选D.如图所示,以D为原点,建立空间直角坐标系,则D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),C1(0,2,1),所以BC1=(-2,0,1).连接AC,易证AC⊥平面BB1D1D,所以平面BB1D1D的一个法向量为a=AC=(-2,2,0).所以所求角的正弦值为cos〈a,BC1〉===.4.在长方体ABCDA1B1C1D1中,B1C和C1D与底面所成角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为()A.B.C.D.解析:选A.以A1为原点建立如图所示的空间直角坐标系,可知∠CB1C1=60°,∠DC1D1=45°,设B1C1=1,则CC1==DD1.所以C1D1=,则有B1(,0,0),C(,1,),C1(,1,0),D(0,1,).所以B1C=(0,1,),C1D=(-,0,).所以cos〈B1C,C1D〉===.5.如图,正方体ABCDA1B1C1D1中,E,F分别是BB1和DD1的中点,则平面ECF与平面ABCD所成的角的余弦值为()A.B.C.D.解析:选B.以点A为坐标原点,建立空间直角坐标系.设正方体的棱长为2,则A(0,0,0),E(2,0,1),F(0,2,1),C(2,2,0),所以CE=(0,-2,1),CF=(-2,0,1).所以平面ECF的一个法向量为n=(1,1,2).设平面ECF与平面ABCD的夹角为θ.因为m=(0,0,1)是平面ABCD的一个法向量,所以cosθ=cos〈m,n〉=.6.若直线l的方向向量a=(-2,3,1),平面α的一个法向量n=(4,0,1),则直线l与平面α所成角的正弦值为________.解析:由题意,得直线l与平面α所成角的正弦值为==.答案:7.如图,在正三棱柱ABCA1B1C1中,AB=AC=AA1=2,E,F分别是BC,A1C1的中点.设D是线段B1C1(包括两个端点)上的动点,若直线BD与EF所成角的余弦值为,则线段BD的长为________.解析:以E为原点,EA,EC所在直线分别为x,y轴,平面BCC1B1内垂直于BC的直线为z轴建立空间直角坐标系,如图.则E(0,0,0),F,B(0,-1,0),设D(0,t,2)(-1≤t≤1),则EF=,BD=(0,t+1,2),设直线BD与EF所成的角为θ,则cosθ===,解得t=1或t=-(舍去),所以BD==2.答案:28.如图,在四棱锥PABCD中,PD⊥底面ABCD,四边形ABCD为正方形,且PD=AB=1,G为△ABC的重心,则PG与底面ABCD所成的角θ的余弦值为________.解析:以D为原点,建立如图所示的空间直角坐标系,则P(0,0,1),A(1,0,0),B(1,1,0),C(0,1,0),所以G,PG=.易知平面ABCD的一个法向量为n=(0,0,1),则cos〈PG,n〉==-,所以PG与平面ABCD所成角的余弦值为=.答案:9.在正方体ABCDA1B1C1D1中,求二面角ABD1C的大小.解:连接AD1,CD1,以点D为坐标原点,建立如图所示的空间直角坐标系.设正方体的棱长为1,则D(0,0,0),A1(1,0,1),C1(0,1,1).由题意知DA1是平面ABD1的一个法向量,且DA1=(1,0,1);DC1是平面BCD1的一个法向量,且DC1=(0,1,1),所以cos〈DA1,DC1〉==.所以〈DA1,DC1〉=60°.结合图形知二面角ABD1C为钝角,所以二面角ABD1C的大小为120°.10.如图所示,在直三棱柱ABCA1B1C1中,∠BCA=90°,点F1是A1C1的中点,BC=CA=2,CC1=1.(1)求异面直线AF1与CB1所成角的余弦值;(2)求直线AF1与平面BCC1B1所成的角.解:(1)如图所示,分别以C为原点,CA,CB,CC1所在直线为x,y,z轴建立空间直角坐标系,由BC=CA=2,CC1=1,得A(2,0,0),B(0,2,0),C1(0,0,1),A1(2,0,1),B1(0,2,1).因为F1为A1C1的中点,所以F1(1,0,1).所以CB1=(0,2,1),AF1=(-1,0,1).所以cos〈CB1,AF1〉===,即异面直线AF1与CB1所成角的余弦值为.(2)因为在直三棱柱ABCA1B1C1中,BB1⊥平面ABC,AC⊂平面ABC,所以BB1⊥AC.因为∠BCA=90°,所以BC⊥AC.因为BC∩BB1=B,BC,BB1⊂平面BCC1B1,所以AC⊥平面BCC1B1.所以CA=(2,0,0)是平面BCC1B1的一个法向量.设直线AF1与平面BCC1B1所成的角为θ,则sinθ=cos〈AF1,CA〉==,所以θ=,所以直线AF1与平面BCC1B1所成的角为.[B能力提升]11.如图所示,已知点P为菱形ABCD外一点,且PA⊥平面ABCD,PA=AD=AC,点F为PC的中点,则二面角CBFD的正切值为()A.B.C.D.解析:选D.如图,连接BD交AC于点O,连接OF,因为四边形ABCD为菱形,所以O为AC的中点,AC⊥BD.因为F为PC的中点,所以OF∥PA,因为PA⊥平面ABCD,所以OF⊥平面ABCD.以O为原点,OB,OC,OF所在直线分别为x轴、y轴、z轴建立空间直角坐标系Oxyz,设PA=AD=AC=1,则BD=,所以B,F,C,D,结合图形可知,OC=,且OC为平面BDF的一个法向量.由BC=,FB=,可求得平面BCF的一个法向量n=(1,,).所以cos〈n,OC〉=,sin〈n,OC〉=,所以tan〈n,OC〉=.12.如图,已知矩形ABCD与矩形ABEF全等,二面角DABE为直二面角,M为AB的中点,FM与BD所成的角为θ,且cosθ=,则=()A.1B.C.D.解析:选C.不妨设BC=1,AB=λ,则=λ.记AF=a,AB=b,AD=c,则FM=b-a,BD=c-b,根据题意,a=c=1,b=λ,a·b=b·c=c·a=0,所以FM·BD=-b2=-λ2,而FM=,BD=,所以cos〈FM,BD〉===,得λ=.故选C.13.(2021·北京市朝阳区模拟)已知在棱长为1的正方体ABCDA1B1C1D1中,点E,F分别是棱BB1,DD1上的动点,且BE=D1F=λ(0<λ≤).设EF与AB所成的角为α,EF与BC所成的角为β,则α+β的最小值为()A.不存在B.C.D.解析:选C.以点D为坐标原点建立空间直角坐标系(图略),则A(1,0,0),B(1,1,0),C(0,1,0),E(1,1,λ),F(0,0,1-λ),则EF=(-1,-1,1-2λ),AB=(0,1,0),BC=(-1,0,0),所以cosα==,cosβ==,所以α=β.又当λ=时,取得最大值,所以αmin=βmin=,所以(α+β)min=.14.在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD.将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.(1)求证:AB⊥CD;(2)若M为AD的中点,求直线AD与平面MBC所成的角的正弦值.(1)证明:因为平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AB⊂平面ABD,AB⊥BD,所以AB⊥平面BCD.又因为CD⊂平面BCD,所以AB⊥CD.(2)解:过点B在平面BCD内作BE⊥BD,如图.由(1)知AB⊥平面BCD,因为BE⊂平面BCD,所以AB⊥BE.以点B为坐标原点建立空间直角坐标系,依题意得B(0,0,0),C(1,1,0),D(0,1,0),A(0,0,1),M,则BC=(1,1,0),BM=,AD=(0,1,-1).设平面MBC的法向量为n=(x0,y0,z0),则即取z0=1,得平面MBC的一个法向量n=(1,-1,1).设直线AD与平面MBC所成的角为θ,则sinθ=cos〈n,AD〉==.故直线AD与平面MBC所成的角的正弦值为.[C拓展探究]15.如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是的中点.(1)设P是上的一点,且AP⊥BE,求∠CBP的大小;(2)当AB=3,AD=2时,求平面AGE与平面ACG所成角的大小.解:(1)因为AP⊥BE,AB⊥BE,AB,AP⊂平面ABP,AB∩AP=A,所以BE⊥平面ABP.又BP⊂平面ABP,所以BE⊥BP.又∠EBC=120°,因此∠CBP=30°.(2)以B为坐标原点,分别以BE,BP,BA所在的直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系.由题意得A(0,0,3),E(2,0,0),G(1,,3),C(-1,,0),故AE=(2,0,-3),AG=(1,,0),CG=(2,0,3),设m=(x1,y1,z1)是平面AEG的一个法向量.由可得取z1=2,可得平面AEG的一个法向量m=(3,-,2).设n=(x2,y2,z2)是平面ACG的一个法向量.由可得取z2=-2,可得平面ACG的一个法向量n=(3,-,-2).所以cos〈m·n〉==.因此平面AGE与平面ACG所成的角为60°.',)
提供12021-2022优化方案数学-选择性必修-第一册会员下载,编号:1700736090,格式为 docx,文件大小为9页,请使用软件:wps,office word 进行编辑,PPT模板中文字,图片,动画效果均可修改,PPT模板下载后图片无水印,更多精品PPT素材下载尽在某某PPT网。所有作品均是用户自行上传分享并拥有版权或使用权,仅供网友学习交流,未经上传用户书面授权,请勿作他用。若您的权利被侵害,请联系963098962@qq.com进行删除处理。

 下载
下载 下载
下载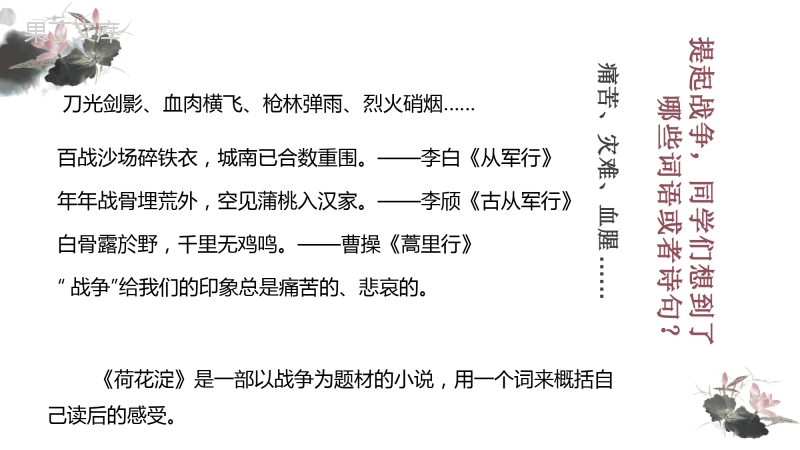 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载