人教版-八年级上册-等腰三角形-优质课件

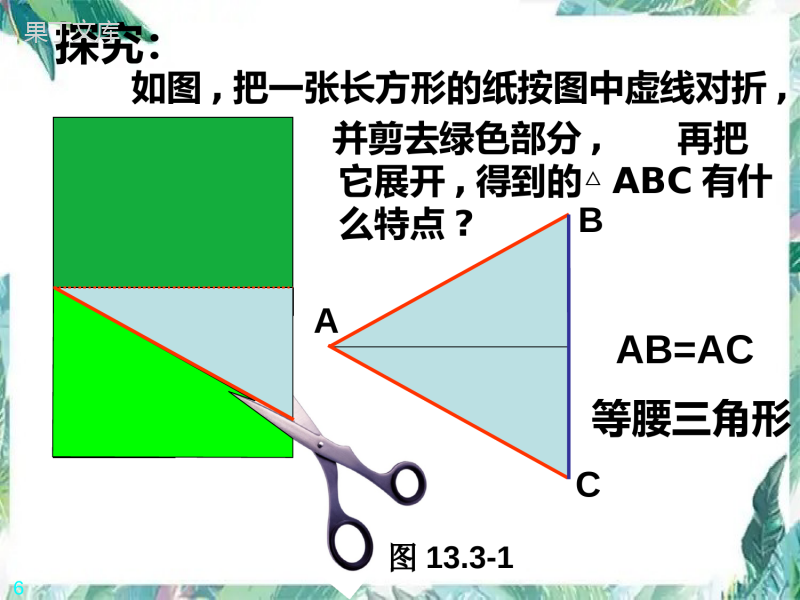
13.3.1等腰三角形义务教育课程标准《人教版》八年级数学上册学习目标1．掌握等腰三角形的概念及性质．2．能灵活应用等腰三角形的概念及性质进行证明和计算．如图,把一张长方形的纸按图中虚线对折,并剪去绿色部分,再把它展开,得到的△ABC有什么特点?ABCAB=AC等腰三角形探究：图13.3-16想一想1、上面剪出的等腰三角形是轴对称图形吗？2、把剪出的等腰三角形ABC沿折痕对折，找出其中重合的线段和角。3、由这些重合的线段和角，你能发现等腰三角形的哪些性质呢？说一说你的猜想。猜想与论证等腰三角形的两个底角相等。已知：△ABC中AB=AC求证：∠B=C分析：1.如何证明两个角相等？2.如何构造两个全等的三角形？猜想ABCDABC则有∠1＝∠2D12在△ABD和△ACD中证明:作顶角的平分线AD，AB＝AC∠1＝∠2AD＝AD（公共边）∴△ABD≌△ACD（SAS）∴∠B＝∠C（全等三角形对应角相等）12ABC则有BD＝CDD在△ABD和△ACD中证明:作△ABC的中线ADAB＝ACBD＝CDAD＝AD（公共边）∴△ABD≌△ACD（SSS）∴∠B＝∠C（全等三角形对应角相等）ABC则有∠ADB＝∠ADC＝90ºD在RtABD△和RtACD△中证明:作△ABC的高线ADAB＝ACAD＝AD（公共边）∴Rt△ABD≌Rt△ACD（HL）∴∠B＝∠C（全等三角形对应角相等）小结：等腰三角形性质：性质1等腰三角形的两个底角相等。性质2等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。（可简记为“三线合一”）（简写成“等边对等角”）；几何语言表示:∵AB=AC∴∠B=∠C(等腰三角形的两个底角相等)∵AB=AC,BAD=CAD∠∠∴BD=CD,ADBC⊥(三线合一)等边对等角如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求△ABC各角的度数1、图中有哪几个等腰三角形？ABCDx⌒2x⌒2x⌒⌒2x△ABC、△ABD、△BDC2、有哪些相等的角？∠ABC=∠ACB=∠BDC、∠A=∠ABD3、这两组相等的角之间有什么关系？∠BDC=2∠A∠ABC+ACB+A=180∠∠°小试牛刀•书上第77页的练习1、2、3如图，在△ABC中，AB=AC，D是AB上一点，延长CA到E，使AE=AD，求证：EDBC.⊥CBDEA拓展提高课后作业•习题13.3第1、3、4、8题．