七年级上册-平均数(1)-教学课件

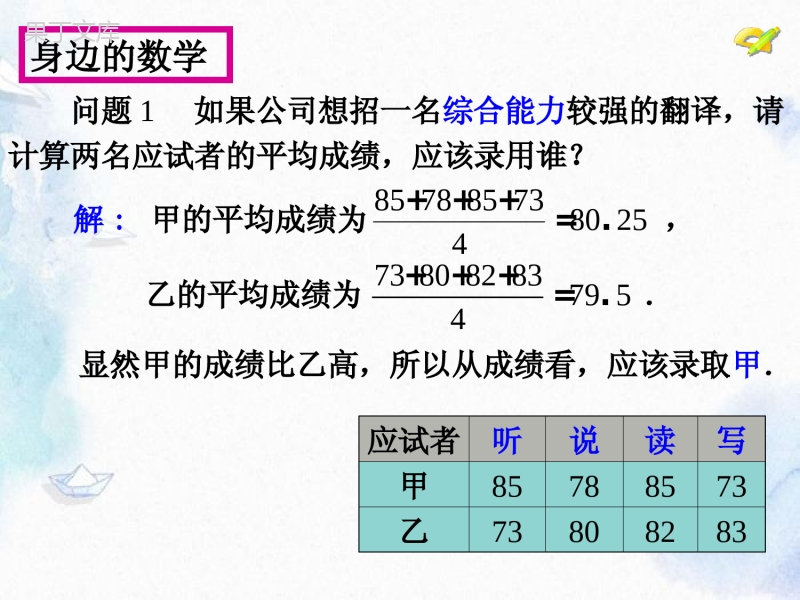
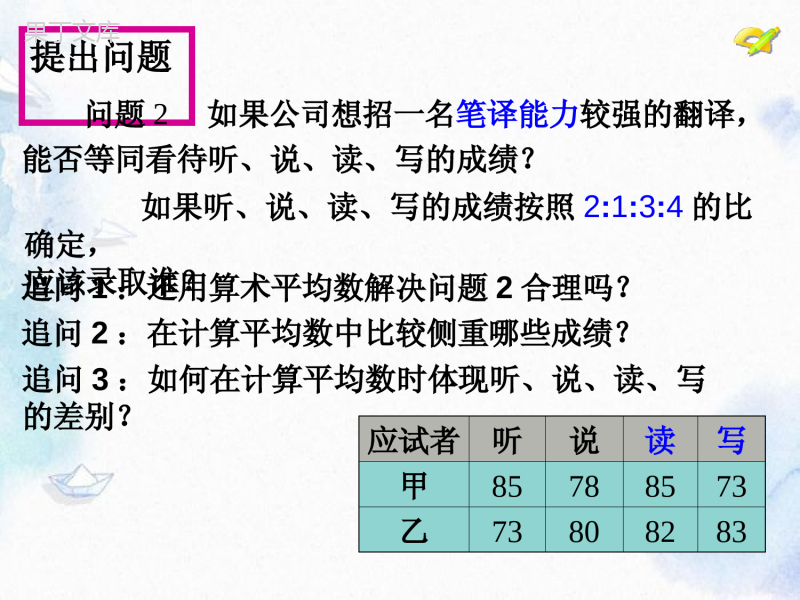
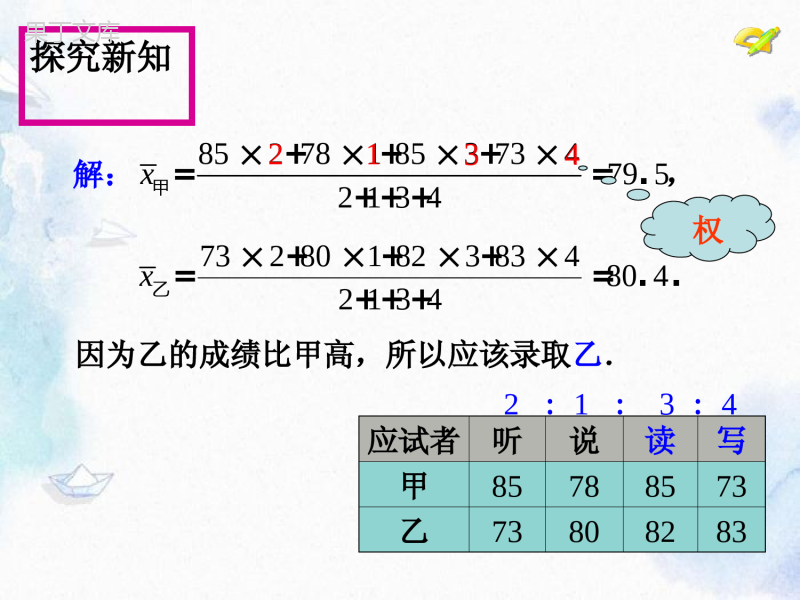
身边的数学乙的平均成绩为．738082837954+++=.显然甲的成绩比乙高，所以从成绩看，应该录取甲．应试者听说读写甲85788573乙73808283解:甲的平均成绩为，8578857380254+++=.问题1如果公司想招一名综合能力较强的翻译，请计算两名应试者的平均成绩，应该录用谁？提出问题问题2如果公司想招一名笔译能力较强的翻译，能否等同看待听、说、读、写的成绩？应试者听说读写甲85788573乙73808283如果听、说、读、写的成绩按照2:1:3:4的比确定，应该录取谁？追问1：还用算术平均数解决问题2合理吗？追问2：在计算平均数中比较侧重哪些成绩？追问3：如何在计算平均数时体现听、说、读、写的差别？探究新知应试者听说读写甲85788573乙738082832:1:3:47328018238348042134+++==..+++x乙因为乙的成绩比甲高，所以应该录取乙．8527818537347952134+++==.+++x甲解：，4312权思考能把这种加权平均数的计算方法推广到一般吗8578857213421379345+++=.+++112212+++=+++nnnxwxwxwxwww探究新知一般地，若n个数x1，x2，…，xn的权分别是w1，w2，…，wn，则叫做这n个数的加权平均数．问题（3）与问题（1）、（2）比较，你能体会到权的作用吗？理解新知问题3如果公司想招一名口语能力较强的翻译，则应该录取谁？应试者听说读写甲85788573乙73808283听、说、读、写的成绩按照3:3:2:2的比确定．权的意义：表示数据的重要程度选手演讲内容演讲能力演讲效果A859595B958595应用新知例1一次演讲比赛中，评委按演讲内容占50％、演讲能力占40％、演讲效果占10％的比例，计算选手的综合成绩（百分制）．试比较谁的成绩更好．解：选手A的最后得分是：选手B的最后得分是：85509540951050401042.5389.590()%%%%%%分95508540951050401047.5349.591()%%%%%%分所以选手B获得第一名，选手A获得第二名．应用新知选手演讲内容(50％)演讲能力（40%）演讲效果(10％)A859595B958595追问：A，B两名选手的单项成绩都是两个95分、一个85分。为什么他们的最后得分不同呢？巩固练习练习某公司欲招聘一名公关人员，对甲、乙两位应试者进行了面试与笔试，他们的成绩（百分制）如下表所示．（1）如果公司认为面试和笔试成绩同等重要，从他们的成绩看，谁将被录取？应试者面试笔试甲8690乙9283（2）如果公司认为，作为公关人员面试成绩应该比笔试成绩更重要，并分别赋予它们6和4的权，计算甲、乙两人各自的平均成绩，谁将被录取？一个“权”的意义:各个数据的“重要程度”.三种“权”的表现形式:(1)比例(2)百分比(3)频数两种平均数的求法：算术平均数加权平均数课堂小结作业:导学案反馈检测预习新课布置作业布置作业应试者测试成绩创新能力计算机能力公关能力A725088B857445C677267拓展应用某广告公司欲招聘职员一名，A，B，C三名候选人的测试成绩（百分制）如下表所示：（1）如果公司招聘的职员分别是网络维护员、客户经理或创作总监，给三项成绩赋予相同的权合理吗？拓展应用某广告公司欲招聘职员一名，A，B，C三名候选人的测试成绩（百分制）如下表所示：（2）请你设计合理的权重，为公司招聘一名职员：①网络维护员；②客户经理；③创作总监．应试者测试成绩创新能力计算机能力公关能力A725088B857445C677267一个“权”的意义:各个数据的“重要程度”.加权平均数中的“权”的三种表现形式:(1)比例(2)百分比(3)频数两种平均数的求法：算术平均数加权平均数课堂小结作业:导学案反馈检测预习新课布置作业布置作业