2022-2023学年湘教版数学八年级上册同步多媒体教学-第2章---全等三角形

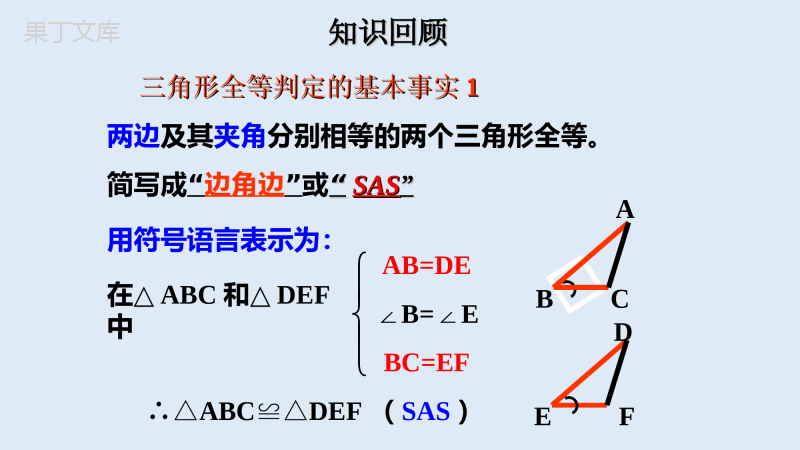
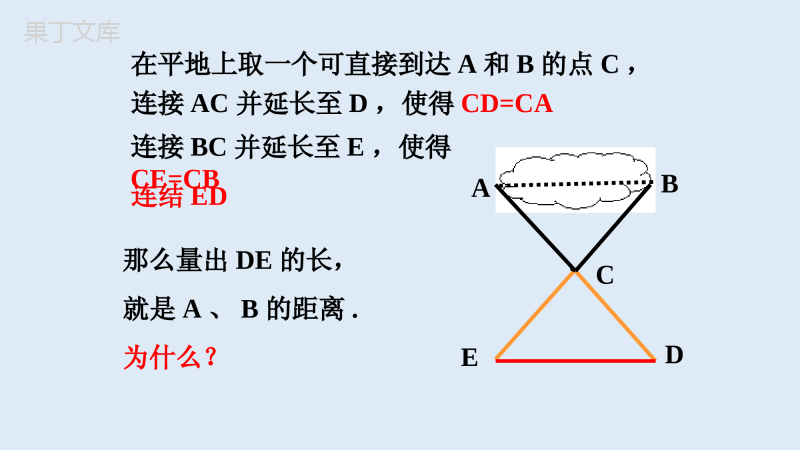
2.5全等三角形学习目标：学习目标：（（11）理解并掌握角角边定理的内容；）理解并掌握角角边定理的内容；（（22）能应用角角边定理证明两个三角形）能应用角角边定理证明两个三角形全等全等..⌒三角形全等判定的基本事实三角形全等判定的基本事实11用符号语言表示为：在△ABC和△DEF中AB=DE∠B=E∠BC=EF∴△ABCDEF≌△（SAS）ABCDEF两边及其夹角分别相等的两个三角形全等。简写成“边角边”或““SASSAS””知识回顾知识回顾⌒问题问题::如图，有一池塘。现要测池塘两端如图，有一池塘。现要测池塘两端AA、、BB的距离，可无法直接达到，因此这两点的距的距离，可无法直接达到，因此这两点的距离无法直接量出。你能帮忙想出办法来吗？离无法直接量出。你能帮忙想出办法来吗？AABBABCED在平地上取一个可直接到达A和B的点C，连接AC并延长至D，使得CD=CA连接BC并延长至E，使得CE=CB连结ED那么量出DE的长，就是A、B的距离.为什么？两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS”）ABCDEF符号语言：∴△ABC≌△DEF（AAS）∠A=∠DBC=EF∠B=∠E证明：在△ABC和△DEF中在△ABC和△A'B'C'中∠∠A=A'∠A=A'∠AB=A'B'∠B=B'∠∴△ABCA'B'C'≌△(ASA)ACBA′C′B′合作学习合作学习两角两角及其及其夹边夹边分别相等的两个三角形全等，简写分别相等的两个三角形全等，简写成“成“角边角角边角”或“”或“ASAASA””。。证明：在△ABE和△ACD中，∴△ABEACD≌△（ASA）．∴AE=AD．∠B=C∠AB=AC∠A=A∠例如图，点D在AB上，点E在AC上，AB=AC，∠B=C∠．求证：AD=AE．ABCDE(公共角)例如图，已知点E，C在线段BF上，BE=CF，ABDE∥，∠ACB=F∠．求证：△ABCDEF≌△．证明：∵BE=CF∴BE+EC=CF+EC，即BC=EF又∵ABDE∥，∴∠B=DEF∠在△ABC和△DEF中，∠B=DEF∠，BC=EF，∠ACB=F∠，∴△ABCDEF≌△（ASA）结论：边角边基本事实有两边和它们的夹角对应相等的两个三角形全等.可以简写成边角边“或SAS”S——S——边边AA————角角合作交流合作交流例1已知:如图，AC=AD，∠CAB=DAB.∠求证:ACB△≌ADB△.ABCD证明:△ACBADB.≌△这两个条件够吗?还要什么条件呢?ABCD证明:在△ACB和△ADB中AC=AD(已知)∠CAB=DAB∠（已知）AB=AB()∴△ACB≌ADB△（SAS）例1已知:如图，AC=AD，∠CAB=DAB.∠求证:ACB△≌ADB△.公共边例2已知：如图，AB和CD相交于O，且AO=BO，CO=DO.求证：△ACO≌BDO.△证明：在△ACO和△BDO中，∴△ACO≌△BDO（）AO=BO∠AOC=∠BOD（）CO=DO对顶角相等SAS证明三角形全等的步骤：证明三角形全等的步骤：1.写出在哪两个三角形中证明全等。（注意把表示对应顶点的字母写在对应的位置上）.2.按边、角、边的顺序列出三个条件.用大括号合在一起.3.证明全等后要有推理的依据.再见再见