人教版-八年级上册-全等三角形(复习课)

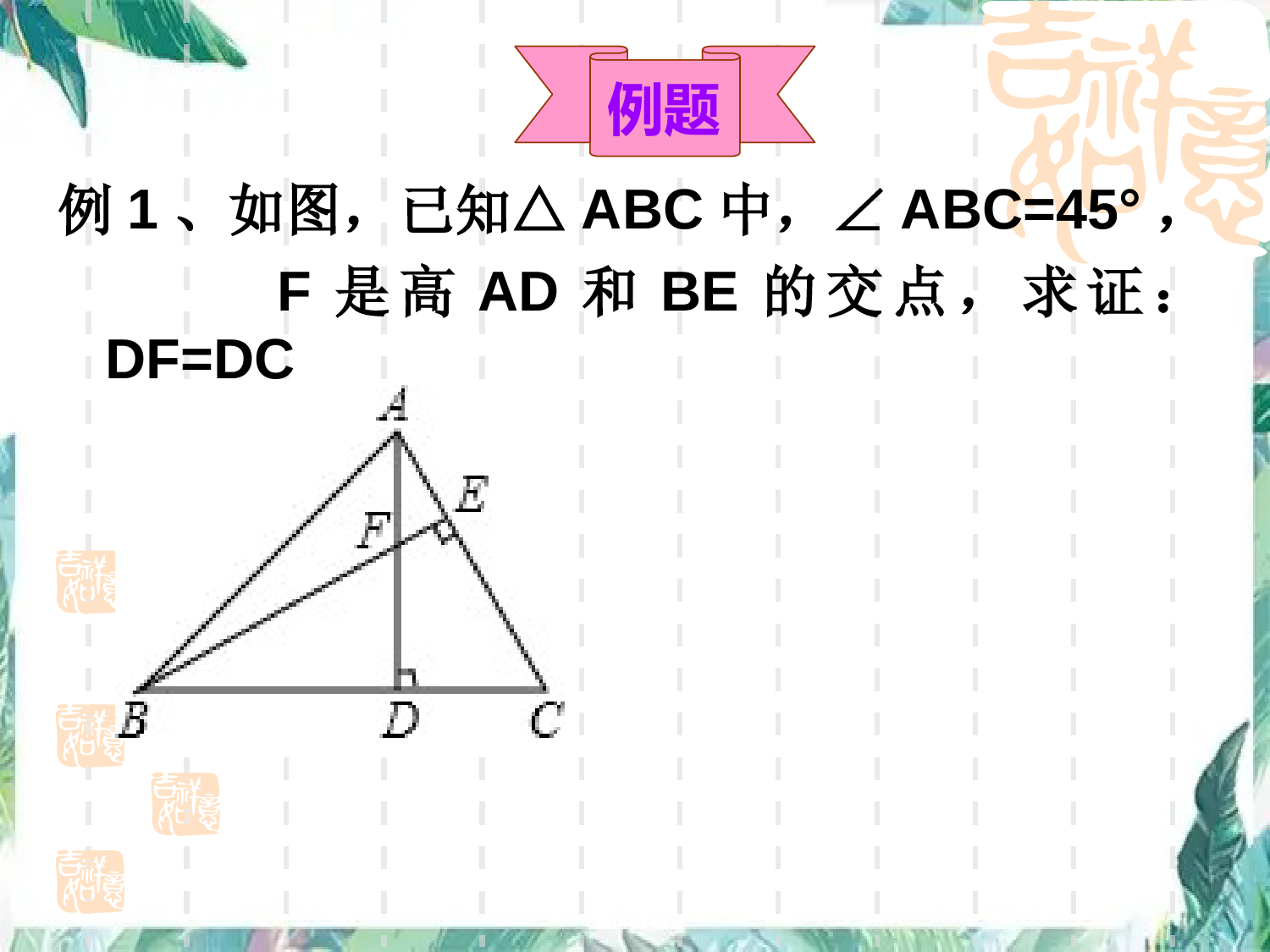
课标要求1、理解全等三角形有关的概念．2、掌握三角形全等的性质与判定.学习目标1、通过全等三角形概念和识别方法的复习，体会辨别、探寻、运用全等三角形的一般方法，体会合作学习的方法。2、培养观察和理解能力，几何语言的叙述能力及运用全等知识解决实际问题的能力。例1、如图，已知△ABC中，∠ABC=45°，F是高AD和BE的交点，求证：DF=DC例题证明：∵AD、BE是△ABC的高，∠ABC=45°∴AD=BD，∠ADC=∠BDF=90°∵∠AFE=∠BFD∴∠DAC=∠DBF在△ADC和△BDF中∴△ADC≌△BDF（ASA）∴DF=DC∠DAC=∠DBFAD=BD∠ADC=∠BDF例2、如图，在平行四边形ABCD中F为CD上一点，且BF=AD，E为DF的中点，∠AEB=90°，过点A作AHBF⊥于H，交BE于G，连接FG（1）若EG=1，AG=3,求BE的长；（2）证明：AG=AD+FGAD=BF∠ADE=BFE∠DE=FE222AGEGAE22231AE22（1）解：∵DC//ABBF=AD∴四边形ABFD是等腰梯形∴∠ADE=BFE∠∵E为DF的中点∴DE=FE在△ADE和△BFE中∴△ADE≌△BFE（SAS）∴AE=BE在RtAEG△中：即：∴BE=AE=（2）证明：延长AD、BE交于点P由（1）△ADEBFE≌△∴∠1=2∠∵∠AEB=90°AHBF⊥又∵∠4=5∠∴∠2=3∠∴∠1=3∠∵AE⊥EG∴EP=EG且AP=AG在△DPE和△FGE中∴△DPEFGE≌△（SAS）∴DP=FG∴AG=AP=AD+DP=AD+FGDE=FE∠6=7∠EP=EG小结