人教版-八年级上-等腰三角形-复习

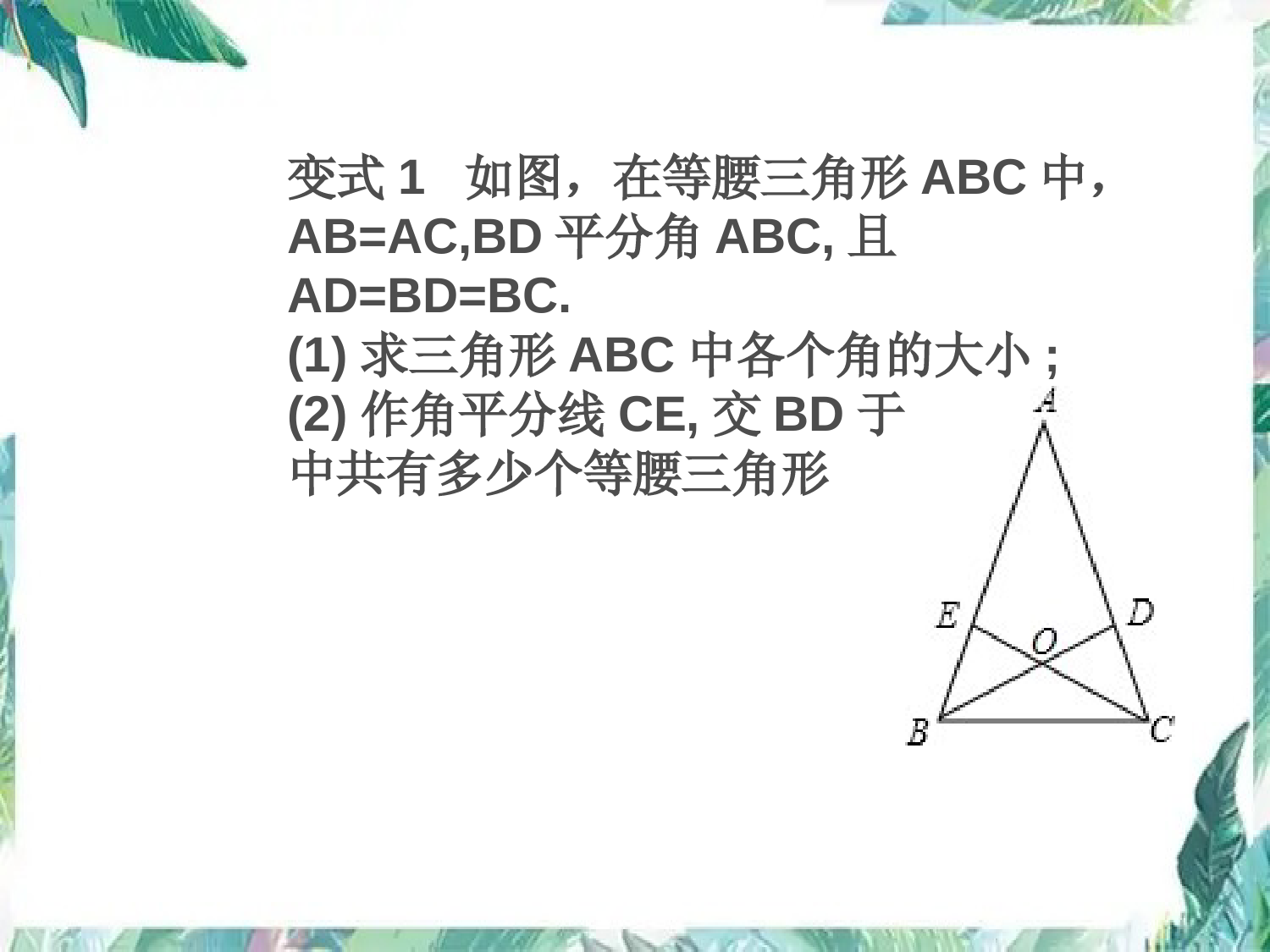
第22课时等腰三角形复习1等腰三角形和等边三角形的定义有（）的三角形叫做等腰三角形，其中（）的三角形叫做等边三角形。知识清单2等腰三角形的性质(1)等腰三角形的两腰（）(2)等腰三角形的两个底角（），简称为（）(3)等腰三角形的（）（）（）互相重合，简称三线合一(4)等腰三角形是（）图形，它有（1）条对称轴，是（）(5)等腰三角形两腰上的（）和（腰和底边相等两边相等相等相等等边对等角顶角的角平分线底边的中线底边的高轴对称顶角的角平分线高中线3等腰三角形的判定(1)定义法：。(2)有（）的三角形是等腰三角形，简称（）4等边三角形的性质(1)等边三角形的(2)等边三角形是轴对称图形，它有（3）条对称轴5等边三角形的判定(1）三条边都相等的三角形是等边三角形(2)三个角都相等的三角形是等边三角形(3)有（一个角是60度）的等腰三角形是等边三角形有两边相等的三角形是等腰三角形两个角相等等角对等边三条边相等，三个角也相等，都等于60度。图19－1例1如图19－1，在等腰三角形ABC中，AB＝AC，AD是BC边上的中线，∠ABC的平分线BG，交AD于点E，EF⊥AB，垂足为F.求证：EF＝ED.探究一等腰三角形的性质的运用变式1如图，在等腰三角形ABC中，AB=AC,BD平分角ABC,且AD=BD=BC.(1)求三角形ABC中各个角的大小;(2)作角平分线CE,交BD于O,那么图中共有多少个等腰三角形探究二等腰三角形的判定例2已知：如图19－2，锐角△ABC的两条高BD、CE相交于点O，且OB＝OC.(1)求证：△ABC是等腰三角形；(2)判断点O是否在∠BAC的平分线上，并说明理由．图19－2探究三等边三角形的性质和判定例3如图，E是等边三角形ABC的AC边上一点，∠1＝∠2，BE＝CD，求证：△ADE是等边三角形．变式3如图19－3，在等边三角形ABC中，D、E分别是BC、AC上的点，且CD＝AE，AD与BE相交于点P.(1)求证：∠ABE＝∠CAD；(2)若BH⊥AD于点H，求证：PB＝2PH.图19－3探究四等腰三角形的多解问题例4已知等腰三角形的一边长为4，另一边长为8，则这个等腰三角形的周长为()A．16B．20或16C．20D．12C探究五等腰三角形的创新应用例5如图1，在△ABC中，∠A＝36°，AB＝AC，∠ABC的平分线BE交AC于E．(1)求证：AE＝BC；(2)如图(2)，过点E作EFBC∥交AB于F，将△AEF绕点A逆时针旋转角α(0°＜α＜144°)得到△AE′F′，连结CE′，BF′，求证：CE′＝BF′；(3)在(2)的旋转过程中是否存在CE′AB∥？若存在，求出相应的旋转角α；若不存在，请说明理由．中考预测等腰三角形的一个角是80°，则它顶角的度数是()A．80°B．80°或20°C．80°或50°D．20°B教材母题如图19－5，在△ABC中，AB＝AD＝DC，∠BAD＝26°.求∠B与∠C的度数．图19－5