中考专题--有中点怎样添加辅助线

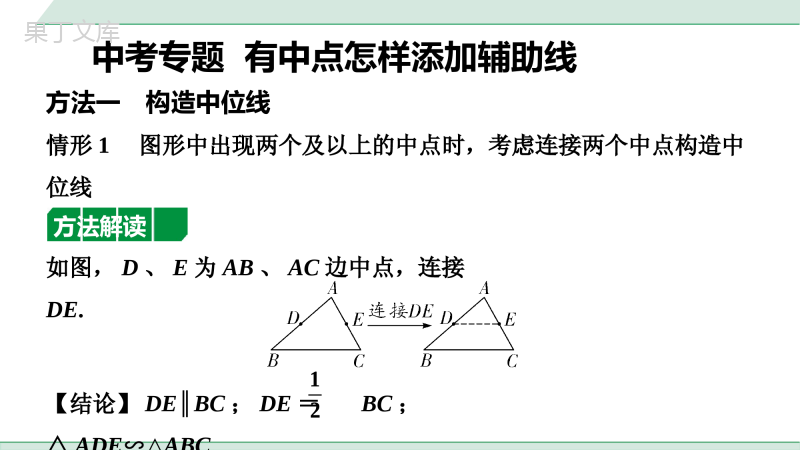
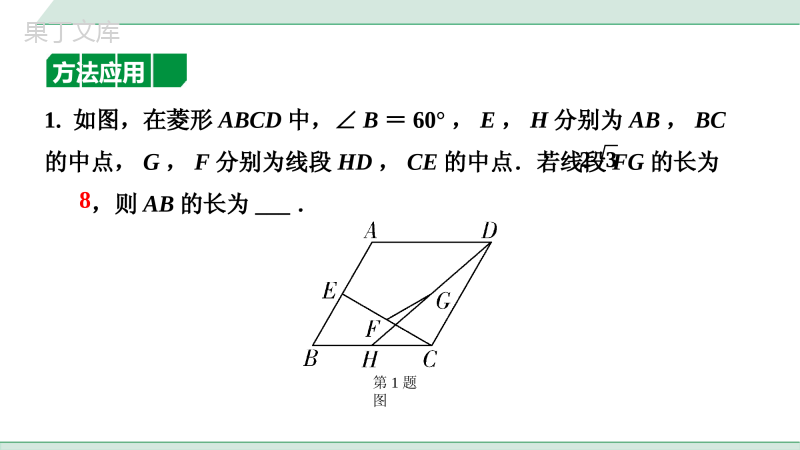
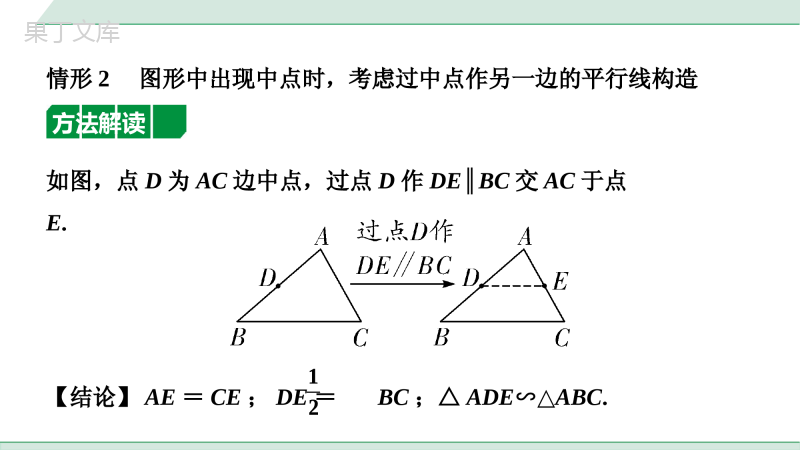
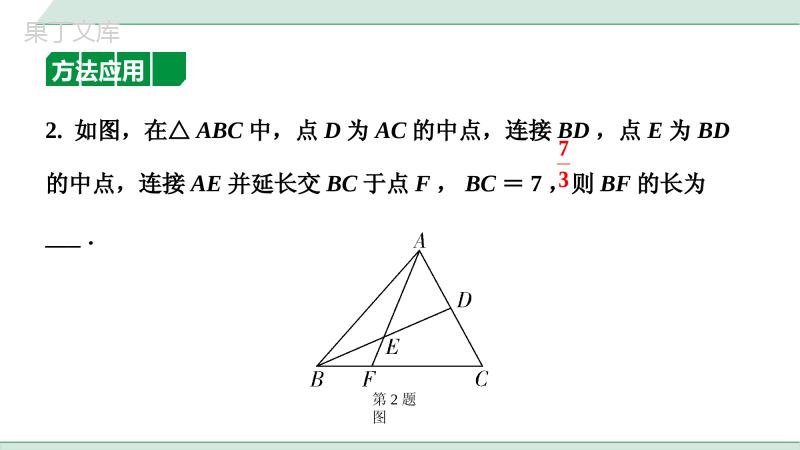
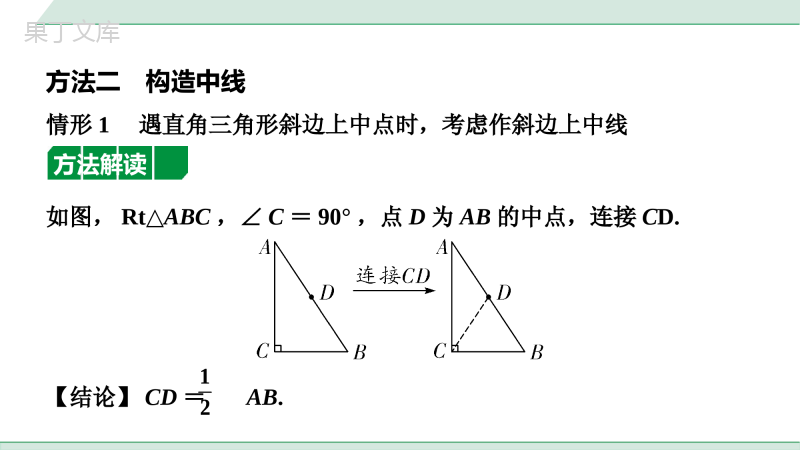
满分技法方法一构造中位线情形1图形中出现两个及以上的中点时，考虑连接两个中点构造中位线方法解读如图，D、E为AB、AC边中点，连接DE.【结论】DE∥BC；DE＝BC；12中考专题有中点怎样添加辅助线12方法应用1.如图，在菱形ABCD中，∠B＝60°，E，H分别为AB，BC的中点，G，F分别为线段HD，CE的中点．若线段FG的长为，则AB的长为___．第1题图23823情形2图形中出现中点时，考虑过中点作另一边的平行线构造方法解读如图，点D为AC边中点，过点D作DE∥BC交AC于点E.【结论】AE＝CE；DE＝BC；△ADE∽△ABC.1212方法应用2.如图，在△ABC中，点D为AC的中点，连接BD，点E为BD的中点，连接AE并延长交BC于点F，BC＝7，则BF的长为___．第2题图7373方法二构造中线情形1遇直角三角形斜边上中点时，考虑作斜边上中线方法解读如图，Rt△ABC，∠C＝90°，点D为AB的中点，连接CD.【结论】CD＝AB.1212方法应用第3题图3.如图，在等腰Rt△ABC中，∠ABC＝90°，D为边AC的中点，E、F分别为AB、BC边上的两点，且DE⊥DF，连接EF，若AE＝4，FC＝3，求EF的长．解：如解图，连接BD.∵D是AC的中点，△ABC为等腰直角三角形，∴∠ABD＝∠CBD＝∠C＝45°，BD＝AD＝CD，BD⊥AC.∵∠EDB＋∠FDB＝90°，∠FDB＋∠CDF＝∴∠EDB＝∠CDF，在△BED和△CFD中，∴△BED≌△CFD(ASA)，∴BE＝CF，∵AB＝BC，BE＝CF＝3，∴AE＝BF＝4，在Rt△BEF中，EF＝＝5.,EBDCBDCDEDBFDC22BEBF第3题图,EBDCBDCDEDBFDC22BEBF情形2遇等腰三角形底边中点时，考虑作底边上中线，利用“三线合一”解题方法解读如图，在等腰△ABC中，点D是底边BC的中点，若连接AD，则AD⊥BC，∠BAD＝∠CAD.方法应用4.如图，若AB＝AC＝3，BC＝4，点E为BC中点，过点E作EF⊥AC于点F，则EF的长为_____．第4题图253253方法三构造中线或倍长中线方法解读①如图，AD是BC边的中线，若延长AD至点E，使得DE＝AD，连接BE，则△ACD≌△EBD.②如图，D是BC边的中点，延长ED至点F，使得DF＝ED，连接CF，则△BDE≌△CDF.方法应用第1题图5.如图，在△ABC中，AD是BC边上的中线，E是AD上一点，连接BE并延长交AC于点F，AF＝EF，求证：AC＝BE.证法一：证明：如解图①，延长AD至点G，使AD＝DG，连接BG，G∵AD是BC边上的中线，∴BD＝CD.在△ACD和△GBD中，∴△ACD≌△GBD(SAS)，,ADGDADCGDBCDBD,ADGDADCGDBCDBD∴BG＝AC，∠CAD＝∠BGD.∵AF＝EF，∴∠EAF＝∠AEF，∵∠AEF＝∠BED，∴∠BED＝∠EAF，∴∠BEG＝∠G，∴BE＝BG，∴AC＝BE.G第1题图证法二：H如解图②，延长ED至点H，使得DH＝DE，连接CH，∵AD是BC边上的中线，∴BD＝CD.在△BDE和△CDH中，∴△BDE≌△CDH(SAS)，∴BE＝CH，∠BED＝∠H.∵AF＝EF，∴∠EAF＝∠AEF，∵∠AEF＝∠BED，∴∠EAF＝∠H，∴AC＝CH，,BDCDBDECDHEDHD第1题图,BDCDBDECDHEDHD第6题图6.如图，在正方形ABCD中，E为AB边的中点，G、F分别为AD，BC边上的点，GE⊥EF，若AG＝1，BF＝2，求GF的长．解：如解图，沿长GE至点H，使得EH＝GE，连接BH，∵E为AB边的中点，∴AE＝BE，在△GEA和△HEB中，∴△GEA≌△HEB(SAS)，,GEHEGEAHEAAEBEH,GEHEGEAHEAAEBE∴GA＝HB＝1，∠EBH＝∠A＝90°，∴F，B，H三点共线，∴HF＝FB＋HB＝3，又∵GE⊥EF，EH＝GE，∴GF＝FH＝3.第6题图H